配备无线通信技术和定位功能的现代移动设备的广泛应用极大方便了用户对互联网的访问，传统的以地域分布和社会关系链接的熟人网络因此在互联网上抽象出了诸如Twi-tter和Facebook等地理社交网络。地理社交网络结合了社交网络与用户的地理空间信息，由于其对现实和虚拟之间裂隙的弥合能力，近年来在地理社交网络中搜索具备高内聚性和紧密空间联系的社区成为了热门研究课题。
考虑一个现实生活中的应用场景，店家为了宣传店铺产品，店家计划邀请一群人举办线下品鉴会。为了方便参会人员到店，店家可以考虑邀请一群住所离店铺不远的人。同时考虑到紧密联系的朋友之间通常具有相似的消费习惯，更容易成为潜在客户，要求这些人中任意一个人至少在其余人中拥有一定数量的朋友。研究人员开发了半径有界k-core（radius bounded k-core，RB-k-core）搜索［1-2］来满足这样的需求，对于任意一个RB-k-core Bi，Bi 中的顶点应该至少在Bi 中拥有k个邻居，且Bi 中所有的顶点落在一个半径为r的圆内。图1展示了一个使用RB-k-core搜索获取参会成员的例子。在k设置为2、r设置为1.5 km的情况下，S 1、S 2和S 3被推荐给店家。
此时店家可能面临一个问题，共有3个社区推荐给他，如何选择参会人员对店家来说是非常困难的。假如邀请3个社区中的所有人，这个品鉴会的成本可能过高，并且与会人员之间相互关系的紧密程度也会被破坏；假如只选择一部分用户，决定选择哪一部分是非常困难的，因为用户并不能直观地感受社区之间的关系。通常顶点规模最大的顶点集合能够覆盖搜索结果集合中尽可能多的顶点，更具备代表性。例如在图1的例子中，S 1中包含5个用户，相比于选择所有7个用户，参会人员间的内聚性得到满足，保证了品鉴会的氛围，又控制了成本；同时尽可能多地覆盖了结果集合，这意味着像John这样未被邀请参加品鉴会的用户有很大可能通过朋友了解店家的咖啡厅。因此本文定义了搜索规模最大的RB-k-core问题（LRBK），旨在从一系列RB-k-cores顶点集合中搜索规模最大的一个作为代表性的RB-k-core提供给用户。
1 相关工作
1.1 社区搜索研究
社区搜索问题最开始由Sozio等［3］提出，旨在搜索一个包含查询顶点的社区。截至目前，在社区搜索上进行的研究已经获得了广泛的应用，例如位置感知营销［4］、影响力分析［5］等。k-core［6］、k-truss［7］和k-clique［8］等模型已成为用户间关系紧密程度的衡量标准，用来搜索内聚社区。k-core因其线性的核分解代价［9］被广泛应用于社区搜索的研究中。Cui等［10］提出了一种局部搜索策略，以评估社区中顶点的内聚程度。Li等［11］基于加权图研究了捕获社区影响力的方法。Huang等［12］和Fang等［13］在属性图上进行了社区搜索问题的研究。然而这些工作都没有考虑用户的地理位置，不能用来解决LRBK问题。
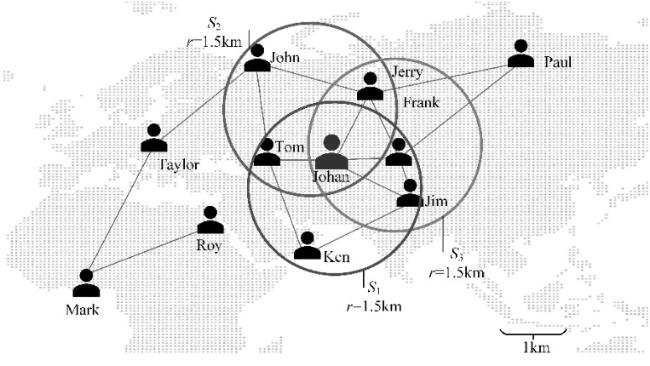
1.2 基于位置的社区搜索研究
通过综合考虑数据的空间信息和社交特征，一些学者基于位置的地理社会网络（location based social network，LBSN）进行了社区搜索研究［14-16］。Zhu等［17］主要研究如何在一个给定的矩形范围内搜索社区。与文献［17］中以矩形覆盖不同的是，Fang等［18］研究了如何搜索一个包含给定查询顶点的社区，要求这个社区被一个半径最小的圆覆盖。Haldar等［19］研究了具备强社交凝聚力的用户密切相关的位置。Zhu等［20］研究了当用户不断移动时如何有效更新地理社会群组。Trung等［21］提出了强化学习模型以完成位置预测任务。Wang等［1-2］的研究与本文工作最相关，他们探索了半径有界k-core搜索问题，该问题指定了结果社区的内聚性和空间分布应该满足的约束，向用户返回多个以给定参数r为半径的圆覆盖的连通k-core社区。以上所有工作都不能直接用来解决LRBK搜索问题。
2 预备知识和问题定义
基于位置的地理社交网络G（V，E，L）是一个无向无权图，其中V是顶点集合，E是边集合，任意边（vi，vj ）∈ E都有vi 、 vj ∈ V，li （xi，yi ）∈ L是一个二维坐标系上的坐标，代表顶点vi 的空间位置。nei G （v）为顶点v在图G中的邻居集合，deg G （v）为顶点v在图G中的顶点度，形式化为deg G （v）=|nei G （v）|。为了介绍规模最大的RB-k-core搜索，首先介绍如下定义。
（1）对于任意顶点v ∈ H，deg G （ H ）（v）≥k；
（2）不存在任何图G的子图Hi 使得H⊆Hi 且满足（1），则称G（H）为G的一个k-core。
为了定义本文的问题，定义core G （k，u）⊆G代表一个包含顶点u的连通的k-core子图。
问题定义：给定图G，查询顶点q、半径r、正整数k。规模最大的RB-k-core搜索问题要求搜索一个顶点集合B max，满足：
（1） G（B max）是一个core G （k，u）；
（2） C（B max）的半径≤r；
（3） 不存在另一个顶点集合Bj 满足（1）、（2）且|B max|<|Bj |。
3 搜索规模最大的RB-k-core
3.1 基本算法
作为当前已知最佳的RB-k-cores搜索算法，RotC+算法被认为是最有效的搜索所有RB-k-cores的方法。其基本思路分为如下几步：
（1）选取以查询顶点q为圆心、2r为半径的圆C（q，2r），从C（q，2r）中搜索一个包含q的连通的k-core子图G（H）；
（2）顺序从H中选取顶点v同C（v，2r）范围内属于H的所有顶点，以r为半径构造二元顶点有界圆集合CB；
（3）如果C（v，2r）中存在一个RB-k-core或者cnes G （ C （ v ，2 r ））（q）<k，回到第（2）步并选取下一个顶点。
（4）以v为极点构造极坐标系，将CB 中所有的圆以其圆心同v构成的直线按与极坐标系0°轴极角大小升序排序；
（5）由于排序CB 后相邻的圆之间顶点差异只有一个，依据这个发现设计了修剪策略，修剪后从剩余的圆中选取顶点构造子图，并在子图中搜索RB-k-cores。
基本算法的一个思路是先使用RotC+算法搜索所有的RB-k-cores，然后从中提取规模最大的一个作为最终结果返回，然而问题并非如此简单。Zong等［22］指出了RotC+算法中的一个谬误，即上述第（5）步提到排序后CB 中相邻的圆之间顶点差异只有一个，实际上相邻圆顶点差异可能是多个，即提出的修剪策略将会失效，RotC+算法不能被直接使用。因而接下来本文介绍了一个可用的RotC+算法的修正版本，并结合它提出了规模最大的RB-k-core搜索问题的基本算法。
算法1.基本算法（Baseline）
输入：地理社交网络G、查询顶点q、半径r、正整数k；
输出：规模最大的RB-k-core B max；
1） B max=Null； R=Null；
2） G（H）←core G （ C （ q ，2 r ））（k，q）；
3） Foreach v∈H do
4） If there exists an RB-k-core B within C（v，2r） then
5） update R by using B； continue；
6） If cnes G （ C （ v ，2 r ））（q）<k then
7） continue；
8） CB =Null；
9） Foreach u∈H do
10） If u≠v and d（u，v）≤2r then
11） insert Cr （u，v） into CB；
12） sort and de-duplication CB；
13） Foreach C（c，r）∈CB do
14） If there exists a core G （ C （ c ， r ））（k，q） B within C（c，r） then
15） update R by using B；
16） B max←the maximal vertices set in R；
17） Return B max；
如算法1所示，基本算法首先初始化顶点集合B max和结果集合R为空，然后从C（q，2r）中选取顶点生成一个包含查询顶点q的连通的k-core子图G（H）。对于H中的任一顶点v，如果在C（v，2r）中存在一个RB-k-core B，使用B更新R，更新方法是如果B是R中任意集合的子集，则丢弃B；如果B是R中任意集合的超集，则使用B覆盖这个集合；否则将B插入到R中，然后修剪顶点v。如果顶点q在G（C（v，2r））中的coreness值小于k，同样修剪顶点v。接下来初始化圆集合CB 为空，选取H中与顶点v距离在2r以内的顶点u构造二元顶点有界圆并插入CB，对CB 中的圆按照极角排序并去重。最后从CB 中按序取出圆C（c，r），并从这些圆中搜索RB-k-core，同时更新R。最后选择R中顶点规模最大的一个赋值给B max作为搜索结果并返回。
复杂度分析：记G（H）=core G （ C （ q ，2 r ））（k，q）中顶点数量为n，边数量为m。算法第4 —7行包含子图构造、核分解和连通性判断，复杂度为O（n（n+m））。由于最多有n 2个圆可能被生成，第9 —14行的复杂度为O（n 2（n+m））。因此算法的总时间复杂度为O（n 2（n+m）+n（n+m））。
3.2 优化算法
基本算法从一系列二元顶点有界圆中预先计算所有的RB-k-cores，再选取其中规模最大的一个来获取结果，这种方法导致了额外的代价，尤其是判断找到的RB-k-core B同已知RB-k-cores集合R之间的关系时引入的开销是没有必要的。优化算法的基本思路是不维护RB-k-cores结果集合R，只保存已知规模最大的结果集B max，同时结合一些修剪和优化策略获取规模最大的RB-k-core。
由于并非所有的二元顶点有界圆中都可能包含有用结果，首先提出了如下性质用以修剪不必要验证的圆。
修剪策略1：根据性质1可知，对于任意的极点v，如果C（v，2r）满足性质1，该极点可以被直接修剪，同时任意的二元顶点有界圆C如果满足性质1也可以直接被修剪。
对于任意一个排序但不去重的圆集合CB，及任意的圆（Ci，Ci +1）∈CB，计算Ci +1同Ci 中顶点差异的一个基本方法是首先搜索得到对应的顶点集合Vi +1和Vi，然后一一对比两个集合中的顶点，这个过程复杂度高达O（|Vi +1|·|Vi |）。为了加速这个过程，本文开发了一种基于生成圆边界顶点的方法快速计算顶点差异。
相邻圆顶点差异快速计算（Q 1）：给定查询半径r和以极点u构造并排序的圆集合CB，对于任意的Ci ∈CB，i∈［1，|CB |］，有Ci =｛｛xi，yi ｝，V（Ci ）｝，其中｛xi，yi ｝是圆心坐标，V（Ci ）是一个顶点集合，存储同u构造的二元顶点有界圆中，圆心坐标在｛xi，yi ｝的所有顶点。差异顶点计算方法是：初始化顶点集合S为以｛x 1，y 1｝为圆心，r为半径的圆中的所有顶点，初始化S Bound=V（C 1）。当圆从Ci 旋转到Ci +1，向S和S Bound中添加属于V（Ci +1）但不属于S的顶点，然后从S和S Bound中扣除属于S Bound且同｛x 2，y 2｝距离超过r的顶点。
算法2.优化算法（Optimal）
输入：地理社交网络G、查询顶点q、半径r、正整数k；
输出：规模最大的RB-k-core B max；
1） B max=Null； G（H）←core G （ C （ q ，2 r ））（k，q）；
2） Foreach v ∈ H do
3） If cnes G （ C （ v ，2 r ））（q）<k or|V（C）|≤|B max| or |core G （ C ）（k，q）|≤|B max| then
4） continue；
5） If there exists an RB-k-core B within C（v，2r） and |B|>|B max| then
6） B max=B； continue；
7） CB =Null；
8） Foreach u ∈ H do
9） If u≠v and d（u，v）≤2r then
10） insert Cr （u，v） into CB；
11） sort CB； initialize S and S bound；
12） Foreach Ci ∈CB，i=［2，|CB |］do
13） maintenance S，G（S） and S Bound；
14） If |S|>|B max| and vertices in V（Ci ） are inserted into S then
15） If there exists a core G （ C （ c ， r ））（k，q） B within G（S）and |B|>|B max| then
16） B max=B；
17） Return B max；
新方法从子图中添加新进入的顶点和边的复杂度是O（1），移除从圆中丢弃的顶点和边也只需要对S Bound中少量顶点进行计算，复杂度是线性的。快速维护相邻圆间顶点差异意味着圆旋转后不需要重新提取顶点构造子图并进行核分解，也就是说问题转化成了在动态图上进行核维护，本文使用了已知最佳的动态核维护方法［23］，其基本思路是基于核分解过程中产生的k-order信息，每次只处理少量可能发生coreness变化的顶点。
结合以上策略，优化算法如算法2所示，首先初始化结果集B max和图G（H）。接下来按照修剪策略1对H中的顶点进行修剪，如果在C（v，2r）中存在规模更大的RB-k-core B，则使用B替换B max。在初始化CB 为空后，根据Q 1生成和排序CB，使用Q 1中的方法维护集合S、G（S）、S bound和G（S）中顶点的coreness。当插入新的顶点到S，且|S|>|B max|，可能从G（S）中找到规模更大的RB-k-core B，如果找到这样的B，则更新B max。迭代以上过程，最后返回B max。
复杂度分析：记G（H）中顶点数量为n，边数量为m。设修剪策略1修剪后顶点数量为n 1（n 1<<n），边数量为m 1（m 1<<m）。优化算法第3— 6行中子图构造、核分解和连通性判断的复杂度为O（n 1（n 1+ m 1））。生成二元顶点有界圆数量至多为（n 1）2，相邻圆顶点差异计算代价为O（1），因此搜索二元顶点有界圆的代价为O（（n 1）2），总时间复杂度为O（（n 1）2+n 1 m 1）。
4 实验结果分析
4.1 实验设置
表1 数据集信息 |
| 数据集 | |V | | |E | | |d ave| |
|---|---|---|---|
| Weeplace | 15 799 | 57 065 | 7.22 |
| Brightkite | 51 406 | 197 167 | 7.67 |
| Gowalla | 107 092 | 456 830 | 8.53 |
| Flickr | 214 698 | 2 096 306 | 19.5 |
| Foursquare | 2 127 093 | 8 640 352 | 8.12 |
表2 参数取值范围及默认值 |
| 参数 | 范围 | 默认值 |
|---|---|---|
| k | 4，7，10，13，16 | 10 |
| r/km | 1，3，5，7，9 | 5 |
| n/% | 20，40，60，80，100 | 100 |
所有实验均使用在每个数据集上随机生成的100个查询顶点进行，并对实验结果取均值以评估算法。定义Baseline代表基本算法，Optimal-代表只包含修剪策略1、不包含Q 1的算法，Optimal代表完整的优化算法。限定算法超时记为ENF。
4.2 实验评估
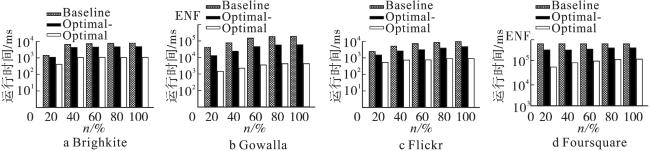
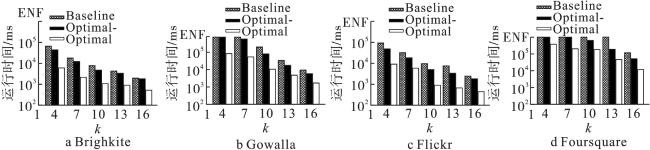
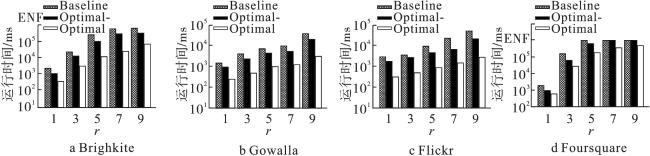
4.2.1 算法效率评估
表3统计了在各数据集上算法的平均执行时间，对比Baseline，Optimal-算法在各数据集上达到了2~4倍算法效率的提升。Optimal算法对比Baseline有约10~20倍的效率提升，证明了本文提出的优化策略的有效性。因为不能在106ms内执行结束，Baseline算法在Foursquare数据集上超时，但优化后的算法保证了解的获取，并优化了约10倍效率。由于具有最高的算法执行效率，Optimal算法是最有效的算法。
表3 算法平均执行时间 (ms) |
| 数据集 | Baseline | Optiaml- | Optiaml |
|---|---|---|---|
| Weeplace | 213.9 | 88.9 | 28 |
| Brightkite | 7 666.3 | 4 744.6 | 1 069.7 |
| Gowalla | 255 652.9 | 101 555.9 | 12 323 |
| Flickr | 9 617.1 | 4 765.2 | 910.3 |
| Foursquare | ENF | 639 352.7 | 181 676.2 |
4.2.2 可伸缩性评估
如图3所示，通过在BK、GW、FK和FS等4个较大数据集上设置其他参数为默认值，数据集规模为20%~100%，这一部分评估了提出算法的可伸缩性。随着数据集规模的增长，所有算法的执行效率都随之降低，原因之一是算法计算了更多的顶点和边；其二是图的密度在逐渐增大。在图3d中，对于Foursquare数据集，即使是20%的规模也比其余3个数据集100%规模更大，约有42万个顶点，因此Baseline算法一直超时。观察图3a—3c可知，3个算法在数据集规模从20%增长到40%时执行时间增长幅度最大，原因是这个阶段增长并参与算法执行的顶点和边对图局部的内聚性影响较大，局部内聚性越大则算法执行时间越长。从80%变化到100%时执行时间增长幅度放缓，这是因为此时再加入运算的顶点和边对图局部的内聚性影响较小。总而言之，各算法在各数据集上都保证了其伸缩性。
4.2.3 参数影响评估
（2）参数r影响评估
通过设定其余参数为默认值，并在1~9范围内变化参数r，图5展示了查询半径r对各算法效率的影响。首先在各数据集上，对于任意算法而言，随着r的增长，算法执行效率都在降低，效率降低的原因是参与算法运算的顶点所处区域是C（q，2r）。显然查询半径r越大，这个区域的范围越大，意味着范围内有更多的顶点，算法也就需要对更多顶点进行处理。在图5a—5d中，当r从1变化到5时，各算法执行时间波动最剧烈，原因是在这个阶段半径的增长带来的顶点数量变化和内聚性变化是最大的。此后当r从5增长到9时，算法效率随顶点数量及内聚性变化的放缓而缓慢降低。表3展示了在Foursquare数据集上，当r取值为5时，Baseline算法超时，如图5d所示，Baseline算法在Foursquare数据集上，r从5变化到9时也发生了超时，这与整体算法效率随r变化而受影响的情况一致。
5 结论
本文提出了规模最大的半径有界k-core搜索问题（LRBK），该问题可用于在地理社会网络中搜索同时满足内聚性、空间约束且规模最大的社区。通过修正过往工作，提出了LRBK问题的基本算法，结合有效的剪枝策略和快速的相邻旋转圆间顶点维护方法提出了优化算法，最后在5个真实世界数据集上评估了提出的算法。考虑到更广泛的应用场景需求，未来计划在地理社会网络上结合用户的属性、时序信息等方面进行查询研究。