Fault diagnosis method of gear based on parameter optimization VMD-KPCA and BP network

Liying JIANG; Qunchen ZHANG; Mingyue GAO; Yingyu ZHANG; He LI

doi:10.3969/j.issn.2095-1248.2024.04.005

Journal of Shenyang Aerospace University >

2024 , Vol. 41 >Issue 4: 41 - 49

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.04.005

Information Science and Engineering

Fault diagnosis method of gear based on parameter optimization VMD-KPCA and BP network

Liying JIANG ,
Qunchen ZHANG ,
Mingyue GAO ,
Yingyu ZHANG ,
He LI

Expand

College of Automation，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2024-04-01

Online published: 2024-09-10

Fold

Abstract

In view of the problems of difficulty in extracting gear fault features and low diagnosis accuracy under noisy environment，a gear fault diagnosis method was proposed，which combined VMD parameter optimization based on comprehensive evaluation indicators，KPCA feature fusion and BP network.Firstly，in order to effectively evaluate the IMF components after VMD decomposition and avoid the problem of manually setting relevant parameters for VMD，a comprehensive evaluation index based on envelope entropy and kurtosis was designed to establish a fitness function for VMD parameter optimization and screen the optimal IMF components.Secondly，after performing VMD decomposition according to the optimal parameters，a multi domain feature set was extracted from the optimal IMF component，and then the KPCA model was used to fuse its features.Finally，fault diagnosis was performed using the BP network model.The experiment shows that under the same experimental conditions，compared with other traditional methods，this method improves the recognition rate of gear faults，with an accuracy of up to 98%，proving the effectiveness of this method.

Key words： gear fault diagnosis; comprehensive evaluation index; variational mode decomposition; whale optimization algorithm; BP network

Cite this article

Liying JIANG , Qunchen ZHANG , Mingyue GAO , Yingyu ZHANG , He LI . Fault diagnosis method of gear based on parameter optimization VMD-KPCA and BP network[J]. Journal of Shenyang Aerospace University, 2024 , 41(4) : 41 -49 . DOI: 10.3969/j.issn.2095-1248.2024.04.005

旋转机械设备广泛应用于航空航天、汽车、机床等行业，而齿轮是旋转设备中最具代表性的关键部件之一。由于齿轮的健康状态直接关系设备能否安全正常运行，更关系到人身安全^［1］，因此尽早识别出齿轮中存在的故障，对保证机械设备的稳定、安全运行具有重要意义。

大多数传统的故障诊断方法只通过时域、频域及时频域来描述振动信号的特征，主要方法有快速傅里叶变换^［2］等，但在复杂工况下采集的振动信号通常是复杂的非平稳信号，故障特征很难被描述。为了解决这个问题，一些信号分解的方法被提出，主要包括经验模态分解及其改进的多元经验模态分解^［3］、集成经验模态分解^［4］、小波变换^［5-6］等。复杂信号通过这些方法可以先分解为若干分量，再通过各种方法描述信号的特征。然而这些分解方法也伴随着端点效应和模态分量混叠的弊端^［7］。Dra-gomiretskiy等^［8］提出的VMD方法将多分量信号分解为带宽固定、中心频率不同的固有模态，不仅具有抗噪能力，且能够降低振动信号的复杂度和不稳定性，有效克服了其他分解方法固有的端点效应和模态分量混叠的问题。武英杰等^［9］针对经验模态分解和局部均值分解的模态混叠问题，提出将VMD应用到风电机组故障诊断中，发现对不平衡故障具有较好的诊断效果。VMD在旋转机械的故障诊断中已被广泛应用，并体现出良好的效果。

然而，VMD的效果与其参数K和

α

的选择相关。在实际工程应用中，这些参数通常需要人为实验确定，耗时费力且很难找到最优参数。当参数选择不准确时，会出现过分解及欠分解的问题，时而影响最后的诊断效果。徐甜甜等^［10］使用经验值设置VMD参数，并结合谱峭度完成IMF选择，判断出齿轮箱轴承故障。Zhang等^［11］提出基于能量准则方法确定分解层数，但该方法对于最优分量的选择不具有自适应性。刘秀丽等^［12］提出一种变分模态分解（VMD）和小波分析相结合的振动信号处理方法，采用中心频率观察法确定VMD分解的K值，但忽视了惩罚因子α对分解结果的影响。张萍等^［13］提出一种基于鲸鱼算法的VMD参数优化方法，并将包络熵作为评价指标，但该方法评价指标单一，不能从多角度综合评价各个IMF分量。

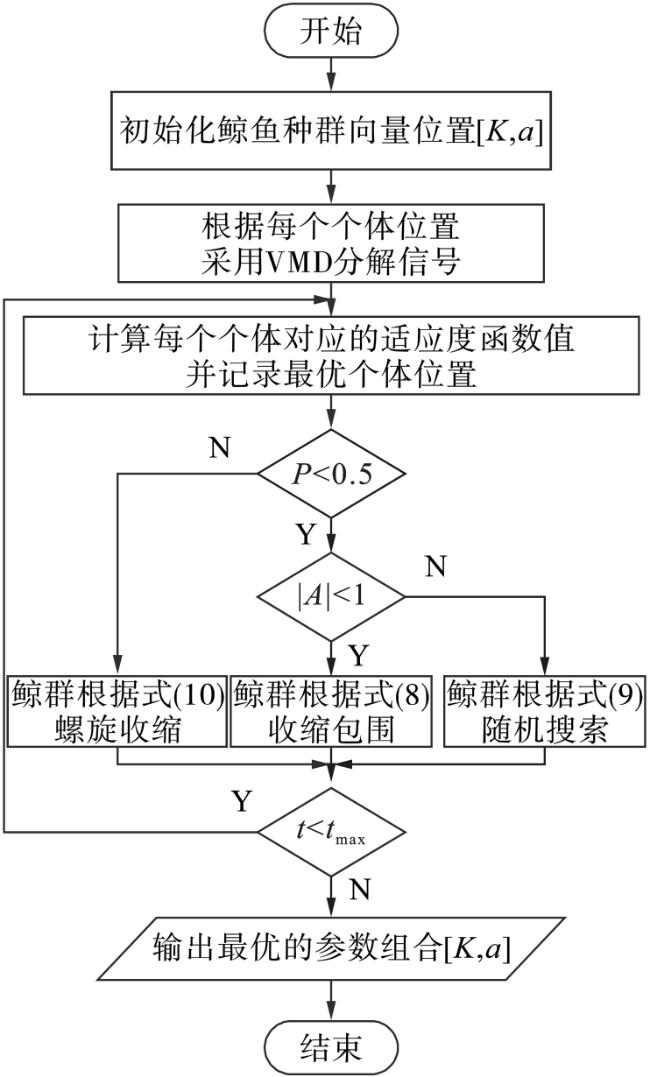
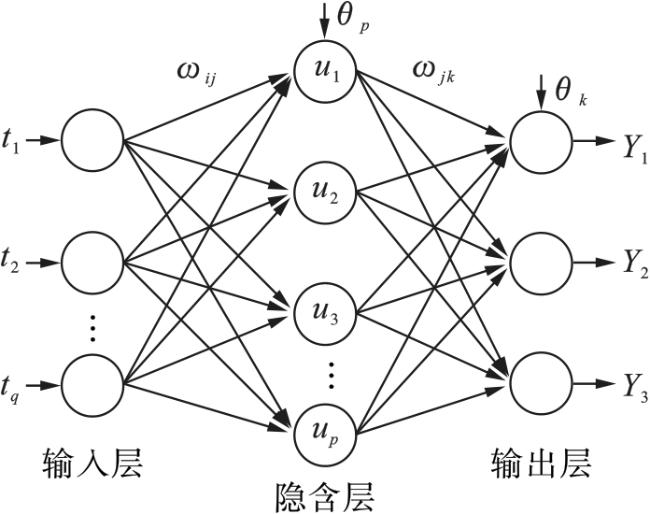
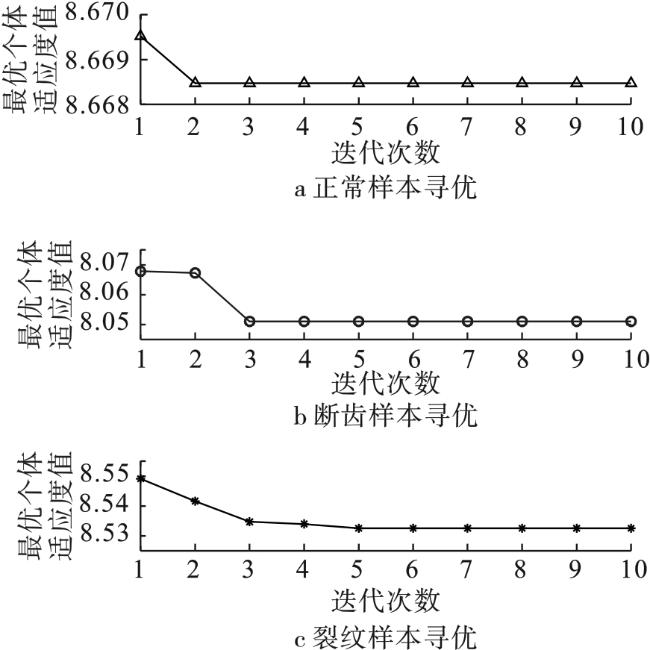
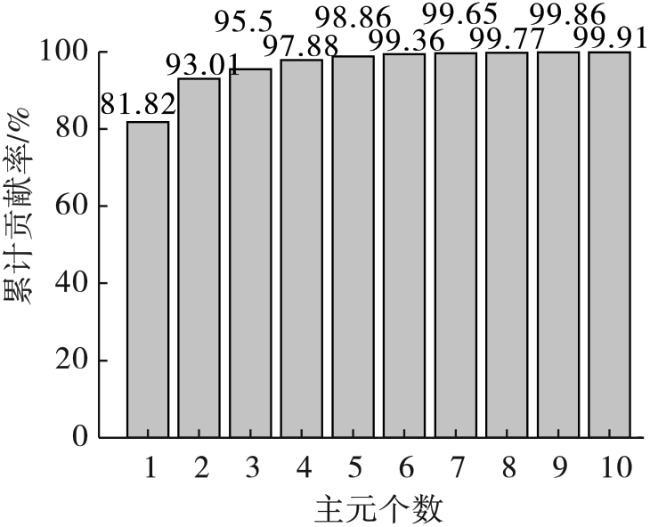
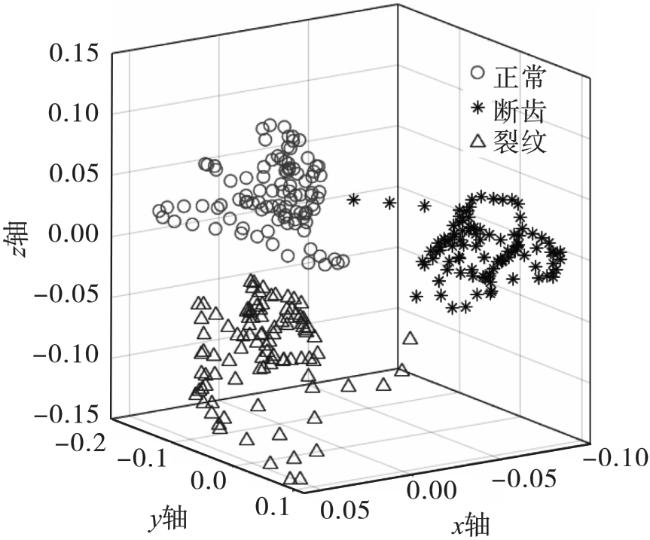
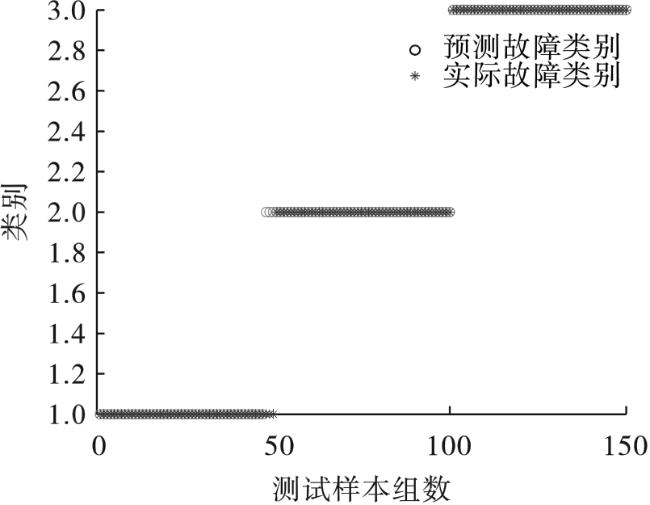
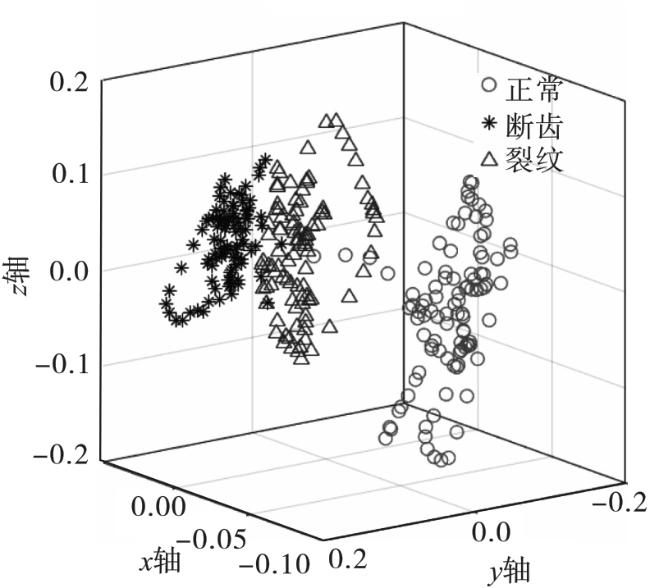
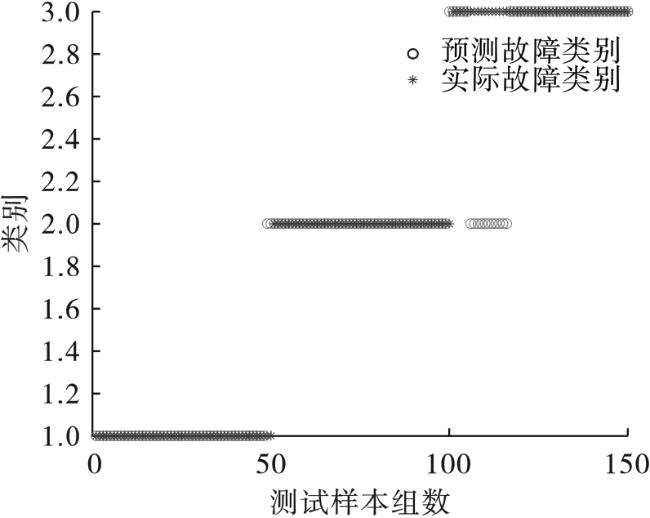
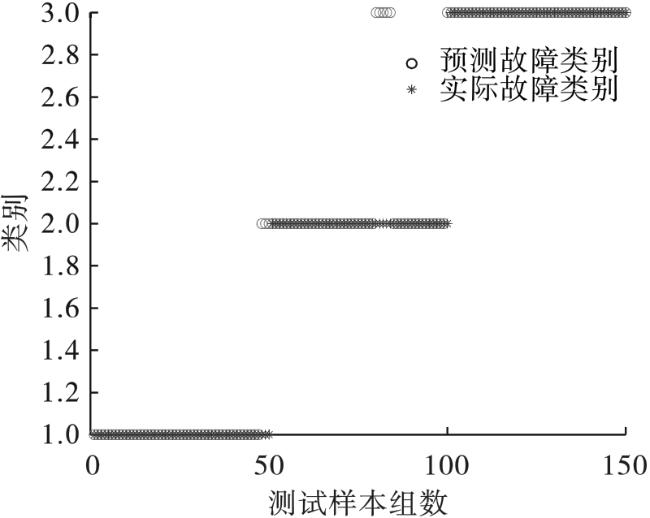
本文提出将包络熵与峭度倒数结合，作为综合评价指标，采用鲸鱼优化算法^［14］（whale optimization algorithm，WOA）优化VMD的参数，在不同状态下分别找到最优参数后取平均值作为最终的最优参数，在线信号按最终的最优参数进行分解，寻找最佳IMF分量并提取其时域、频域、时频域特征后，用训练好的KPCA模型完成特征的融合，最后导入训练好的BP网络中得到诊断结果，并通过与未经KPCA特征融合及未优化VMD的诊断结果进行对比的方式来证明本文方法的有效性。

1 基于综合评价指标的VMD参数优化

1.1 VMD算法原理

对信号采用VMD分解要先建立变分模型，通过迭代更新找到变分模型的最优解，即原始信号f分解得到的K个模态分量（IMF）及其中心频率的最优解。

具体步骤如下：

（1）对每个模态分量

u k (t)

经过Hilbert变换得到其单边频谱后，再添加指数项

e - j ω k t

，得到相应的基频带。

（2）进行高斯平滑处理，得到各个模态分量

u k (t)

的估计带宽，要求每个模态分量的估计带宽之和最小且所有的模态分量之和等于原始信号。根据上述要求建立的变分模型为

m i n {u k}, {ω k} ∑ k = 1 K ∂ t δ (t) + j π t * u k (t) e - j ω k t 22 s . t . ∑ k = 1 K u k (t) = f

（1）

式中：

δ t

为脉冲函数；j为复数单位；t为时间；“

*

”为卷积符号；｛

u k

｝=｛

u 1, u 2, . . ., u K

｝为VMD分解得到的K个模态分量；｛

ω k

｝=｛

ω 1, ω 2, . . ., ω K

｝为每个模态分量对应的中心频率；

22

为求二范数的平方；f为待分解的原始信号。

（3）求解变分模型时，为了求解式（1）的约束最优问题，先引入拉格朗日（Lagrange）算子

λ

和二次惩罚因子

α

，将约束最优问题转化为无约束问题^［8］。Lagrange增广函数为

L u k, ω k, λ = α ∑ k = 1 K ∂ t δ (t) + j π t * u k (t) e - j ω k t 22 + f (t) - ∑ k = 1 K u k (t) 22 + λ (t), f (t) - ∑ k = 1 K u k (t)

（2）

为了求出增广Lagrange函数的鞍点，求解过程中将｛

u k 1

｝、｛

ω k 1

｝、

λ 1

初始化后输入，经过交替方向乘子算法迭代更新各个模态分量及其对应的中心频率。

根据上述过程可以得出，VMD分解的效果与模态分量个数K和惩罚参数

α

有关，因此，K和

α

的选择是至关重要的。

1.2 综合评价指标及适应度函数

针对VMD分解参数难以确定的问题，本文采用鲸鱼优化算法优化VMD的分解层数K和惩罚因子

α

，优化过程中的关键问题是适应度函数的构建。本文通过结合包络熵与峭度，提出一种新的综合评价指标，从而对各IMF分量进行评价，计算各IMF分量的综合评价指标值并将其最小值作为寻优的适应度值。

包络熵是一种用于描述信号复杂程度的物理量。包络熵值越小，信号的复杂度就越小，自我相似性就越高^［15］。

峭度描述信号的冲击特性。峭度值越大，冲击特性越强，故障特征信息越丰富，也更容易提取到故障特征。

为使VMD分解后的IMF分量包含较多的特征信息，本文提出将这两种指标进行结合，构建一种新的综合评价指标C，对各IMF分量进行评价，其计算公式为

C k = E p (I M F k) + 1 / K u r t o s i s (I M F k)

（3）

式中：

E p (I M F k)

表示第k（

k = 1,2, ⋯, K

）个IMF分量的包络熵值，其计算公式如式（4）所示。

E p (I M F k) = - ∑ i = 1 R ε (j) ∑ i = 1 R ε (i) l g ε (j) ∑ i = 1 R ε (i)

（4）

式中：R为IMF分量序列的长度；

ε

为第k个IMF分量的Hilbert包络信号。

K u r t o s i s (I M F k)

为第k（

k = 1,2, ⋯, K

）个IMF分量的峭度值，其计算公式如式（5）所示。

K u r t o s i s (I M F k) = E (I M F k - μ k) 4 σ k 4

（5）

式中，E（）表示数学期望；

μ k

为IMF分量的均值向量；

σ k

为IMF分量的标准差。

显然，

C k

值越小，对应的IMF分量冲击性和稳定性越好，故障特征信息越丰富。因此，将适应度函数定义为

h = m i n (C 1, C 2, ⋯, C K)

（6）

1.3 基于WOA的VMD参数优化流程

基于鲸鱼算法的VMD参数优化流程如图1所示，具体步骤如下：

显示原图|下载原图ZIP|生成PPT

图1 基于WOA优化VMD参数流程图

步骤1：初始化。导入齿轮每种状态下的历史振动数据，设置VMD参数K和

α

的最大值

K m a x

、

α m a x

和最小值

K m i n

、

α m i n

，以及鲸鱼种群的个体数量I、迭代次数

t m a x

、当前迭代次数t（t的初始值为0）等参数及初始化鲸鱼种群中个体的位置向量

X = K, α T

，其初始化公式为

X i 0 = r ⋅ (u b - l b) + l b i = 1,2, ⋯, I

（7）

式中：

r

为0~1之间的随机向量；参数边界最小值

l b = K m i n, α m i n T

，最大值

u b = K m a x, α m a x T

；“∙”为两个向量对应元素的乘法。

步骤2：确定初值最优个体

X 0 *

。历史振动数据分别按照种群中每个个体的位置

X i 0

进行VMD分解。并根据式（4）、式（7）计算每个个体的适应度值

h i 0

，选取适应度值最小

h 0 * = m i n (h 10, h 20, ⋯, h I 0)

的个体作为初始最优个体

X 0 *

。

步骤3：种群位置更新。根据［0，1］之间的随机数p及系数向量 A，每个个体按照以下3种方式对位置进行更新。当随机数

p < 0.5

，且向量 A 的模值

A < 1

时，选择最佳搜索代理方式进行收缩包围，其第i个个体位置

X i t

的更新公式为

X i t + 1 = X t * - A ⋅ C ⋅ X t * - X i t

（8）

式中：系数向量

A = a (2 r 1 - 1)

，

C = 2 r 2

；

a = 2 - 2 t / t m a x

，在迭代过程中从2线性衰减至0；

r 1

、

r 2

均为［0，1］中的随机向量；| |表示对向量中的每个元素取绝对值；

X t *

为当前最优个体位置；

C ⋅ X t * - X i t

为猎物与当前鲸鱼个体间的相对距离。这里， 1 表示单位列向量。当

p < 0.5

且

A ≥ 1

时，选择随机搜索代理方式进行迭代更新。个体位置

X i t

的更新公式为

X i t + 1 = X r a n d - A ⋅ C ⋅ X r a n d - X i t

（9）

式中：

X r a n d

为随机选取鲸鱼个体的位置向量；

C ⋅ X r a n d - X i t

代表当前鲸鱼个体与其他任意鲸鱼个体的相对距离。当

p ≥ 0.5

时，选择螺旋收缩方式进行迭代更新。个体位置

X i t

的更新公式为

X i t + 1 = e b l c o s (2 π l) X t * - X i t + X t *

（10）

式中：b为定义对数螺线形状的常数；l为［-1，1］之间的随机数；

X * (t) - X i (t)

代表当前鲸鱼个体与最优鲸鱼个体间的距离。

步骤4：计算更新后各个体

X i t + 1

的适应度值，确定当前的最优个体

X t + 1 *

及其适应度值

h t + 1 *

。当

h t + 1 * ≤ h t *

时，

X t + 1 *

为最优个体；当

h t + 1 * > h t *

时，则

X t + 1 * = X t *

（最优保留）。

步骤5：判断是否达到最大迭代次数，若满足则循环结束，将当前最优个体

X t + 1 *

作为最优参数结果输出。否则，返回步骤3继续循环迭代。

2 基于KPCA与BP网络的故障诊断方法

根据优化得到的最优参数进行VMD分解后，为了减少数据的维度并同时保留尽可能多的有用信息，本文采用基于KPCA与BP网络相结合的故障诊断方法。

2.1 IMF分量筛选及特征提取

一旦确定好最优VMD参数

K *

、

α *

后，就可以对齿轮振动样本数据进行VMD分解，得到

K *

个IMF分量。本文根据式（4）计算每个分量的综合评价指标，并选取最小的综合评价指标所对应的IMF分量作为最优分量

I M F *

。

针对单一特征指标无法准确全面描述振动信号的故障特征，本文提出对最优IMF分量

I M F *

提取时域（如方差、均值、方根幅值、均方根值等）、频域（平均频率、重心频率等）、时频域（能量熵等）特征。

2.2 基于KPCA的特征融合模型构建

KPCA的核心思想是通过核函数将原始空间中的数据通过核函数映射到高维空间中，使低维空间中线性不可分的数据在高维空间中线性可分^［16］，再通过主成分分析（PCA）将高维空间中的数据映射到另一个低维空间中，从而实现数据非线性特征融合。

应用KPCA对特征进行融合的关键问题是确定KPCA模型，即利用历史数据确定变换矩阵。构建KPCA模型的主要步骤如下：

步骤1：构建特征样本集。对齿轮历史数据（包括正常状态和故障状态）提取特征向量

s

，构建特征数据集

S = {s 1, s 2, ⋯, s M}

，其中，M为样本数。

步骤2：标准化处理。运用特征样本均值向量

s ¯ = 1 M ∑ i = 1 M s i

和特征样本方差

σ 2 = 1 M ∑ i = 1 M s i - s ¯ 2

对特征集S中的样本进行标准化处理，处理后的数据集记为

S^= {s^1, s^2, ⋯, s^M}

。

步骤3：构建核矩阵 Q。使用样本特征向量集

S^

构建核矩阵 Q，其表达式如下

Q = Q (s^1, s^1) ⋯ Q (s^1, s^M) ⋮ ⋱ ⋮ Q (s^M, s^1) ⋯ Q (s^M, s^M) M × M

（11）

当选择高斯径向基核函数时，核矩阵元素

Q (s^i, s^j)

计算公式为

Q (s^i, s^j) = e x p - s^i - s^j 2 2 γ 2

（12）

式中：

γ

为核宽度。

步骤4：确定KPCA变换矩阵 W。对核矩阵 Q 进行特征值分解，将特征值按从大到小排列，即

λ 1 ≥ λ 2 ≥ ⋯ ≥ λ M

，对应的特征向量为

α 1

，

α 2

，...，

α M

。若前q个主元的累计贡献率

∑ i = 1 q λ i / ∑ i = 1 M λ i

达到预设要求（通常取85%）时，KPCA变换矩阵 W 为

W = α 1 α 2 ⋯ α q M × q

（13）

显然，建立KPCA特征融合模型就是确定样本均值向量

s ¯

、特征样本方差

σ 2

和变换矩阵 W。对于任一标准化后的特征样本

s^

，其在高维空间的核向量

v = Q (s^1, s^) Q (s^2, s^) ⋯ Q (s^M, s^) T

，则

s^

的主元得分（即融合后的特征向量）

t = t 1 t 2 ⋯ t q T

为

t = W T v

（14）

2.3 基于BP网络的故障诊断模型构建

为了实现对滚动轴承故障的识别，本文构建一种基于BP网络的故障诊断模型，其结构如图2所示。输入层为主元得分向量t，即融合后的特征向量；输出层为故障类别，假设齿轮共正常、断齿、裂纹3种状态，则输出层节点数为3，可将正常状态标记为100；断齿状态标记为010；裂纹状态标记为001。

显示原图|下载原图ZIP|生成PPT

图2 故障诊断BP网络结构图

训练时，带标签的输入训练集 TT 是由标准化后的特征样本

s^i

在核主元空间的得分向量

t i (i = 1,2, ⋯, M)

构成，即

T T M × q = t 1 t 2 ⋯ t M T = (W T Q) T = Q W

（15）

2.4 故障诊断流程

对一个在线样本进行故障诊断的具体步骤为：

步骤1：将该在线样本按寻优好的最优参数

[K *, α *]

进行VMD分解。

步骤2：筛选出最优IMF分量并对其进行特征提取，得到特征向量

s n e w

。

步骤3：标准化处理。通过

s ¯

和

σ 2

对

s n e w

进行标准化处理，处理后的特征向量记为

s^n e w

。

步骤4：根据式（14）计算主元得分

t n e w

，即：

t n e w = W T v n e w

。其中

v n e w

为

v n e w = Q (s^1, s^n e w) Q (s^2, s^n e w) ⋯ Q (s^M, s^n e w) T

（16）

步骤5：将经过特征融合后的特征向量

t n e w

导入训练好的BP网络中，得到该样本的诊断结果。

3 实例验证

3.1 原始数据

本文的试验数据是利用江苏千鹏QPZZ-II型旋转机械故障模拟试验台测得，如图3所示。其中，齿轮箱由55齿的主动齿轮和75齿的从动齿轮组成，采用电子放电的方法将裂纹和断齿故障分别引入从动齿轮，齿轮箱顶部安装传感器。

显示原图|下载原图ZIP|生成PPT

图3 QPZZ-II旋转机械故障模拟试验台

本试验台的数据采样频率设置为5 kHz。采集到的数据加入-10 dB的高斯白噪声后，每种工作状态中选取100组样本数据，每组样本包括1 024个采样点。

3.2 WOA优化VMD

本文分别对3种不同状态的齿轮历史数据进行VMD优化，其中WOA种群规模为10；最大迭代次数为10；K的取值范围为［3，10］，且为整数；α的取值范围为［100，2 500］。优化过程中随着迭代次数的增加而得到的收敛曲线如图4所示，优化后的结果如表1所示。

显示原图|下载原图ZIP|生成PPT

图4 随迭代次数的最优个体适应度值变化曲线

表1 不同状态下得到的最优VMD参数

数据类型	模态个数K	惩罚因子α
正常状态	10	2 497
裂纹故障	10	2 500
断齿故障	9	2 500

同时，为确保实际工程意义，使最后得到的最优参数对不同状态的齿轮数据具有通用性，故对不同状态下最优的K和α取平均值作为最终的VMD参数。由表1可知，K^* =10，α^*=2 499。

3.3 KPCA特征融合

利用最优参数

[K *, α *]

对每个样本进行VMD分解后，根据综合评价指标筛选出最优的IMF分量。以正常状态的前3个样本为例，其对应的IMF分量的适应度值如表2所示。

表2 正常状态下前3个样本各IMF分量的适应度值

序号

样本1

样本2

样本3

IMF1

IMF2

IMF3

IMF4

IMF5

IMF6

IMF7

IMF8

IMF9

IMF10

9.59

9.55

9.47

9.70

10.04

9.80

9.54

10.51

9.67

9.43

10.84

9.28

10.40

9.51

9.67

9.86

9.77

9.55

10.52

10.02

10.46

9.62

9.35

9.49

10.33

9.38

9.40

9.76

9.56

9.55

在表2中，样本1的IMF10为最优分量，对应的适应度值为9.43；样本2的IMF2为最优分量，对应的适应度值为9.28；样本3的IMF3为最优分量，对应的适应度值为9.35。

对最优IMF分量进行时域、频域、时频域特征的计算，综合考虑各个特征指标在振动信号敏感度和稳定性方面的优势，本文选择方差、均值等13个时域特征，平均频率、重心频率等4个频域特征，以及1个能反映能量分布均匀性且可体现IMF分量所含频率复杂程度的时频域特征-能量熵，从而构建多域特征集。每种状态取50个样本的特征集作为训练集，每种状态取另50个样本的特征集作为测试集。

在构建多域特征集后，先进行KPCA模型的训练。其中的主元累积贡献率分布如图5所示，图中只列出了前10个主元。由图5知前3个主元的累积贡献率已经达到了95%以上，故选取前3个主元，将特征融合成三维，KPCA模型训练完毕。

显示原图|下载原图ZIP|生成PPT

图5 主元累积贡献率分布图

测试集经过KPCA模型进行特征融合后的三维特征分布如图6所示，由图6可知3种状态类内的聚类特性较好，类间的差异性距离较大，特征分类较明显。

显示原图|下载原图ZIP|生成PPT

图6 WOA-VMD-KPCA特征分布图

3.4 BP网络诊断

先进行BP网络模型的训练。对训练集经KPCA模型后得到的融合特征集按状态划分为1、2、3共3种标签，其中1对应100；2对应010，3对应001。对带标签的融合特征集完成BP模型的训练。

测试集经KPCA模型后再输入到训练好的BP网络模型中进行故障诊断和分类识别，得到的测试集分类诊断结果如图7所示。由图7可知，诊断准确率高达98%。

显示原图|下载原图ZIP|生成PPT

图7 本文方法（WOA-VMD-KPCA-BP）诊断结果图

3.5 对比试验

为验证本文所提出模型的准确性及适用性，现将本文提出的模型与中心频率法^［17］VMD-KPCA-BP及WOA-VMD-BP两种模型进行对比分析。

当采用中心频率法VMD-KPCA-BP模型时，3种状态下经中心频率法确定的分解层数K值均为3，惩罚因子选用默认值α=2 000，进而进行VMD分解，对最优IMF分量提取上文所述的多域特征后，再利用此特征集通过上文方法训练KPCA特征融合模型和BP网络诊断模型。测试集经KPCA模型的三维特征分布如图8所示。

显示原图|下载原图ZIP|生成PPT

图8 中心频率法VMD-KPCA特征分布图

对比图6、图8可知，本文提出的WOA-VMD-KPCA模型对于特征分类取得了更显著的效果。测试集的分类诊断结果如图9所示。

显示原图|下载原图ZIP|生成PPT

图9 中心频率法VMD-KPCA-BP模型诊断结果图

由图7和图9可知，中心频率法VMD-KPCA-BP模型的诊断准确率为90.67%，低于本文所提出模型准确率，证明了基于综合评价指标的WOA-VMD方法的有效性。

当采用WOA-VMD-BP模型时，利用通过WOA算法得到的最优参数进行VMD分解，对最优IMF分量提取上文所述的多域特征后，直接利用此特征集通过上文方法构建BP网络诊断模型，测试集的分类诊断结果如图10所示。

显示原图|下载原图ZIP|生成PPT

图10 WOA-VMD-BP模型诊断结果图

由图10可知，WOA-VMD-BP模型的诊断准确率为94%，低于本文所提出模型准确率，证明了KPCA特征融合方法的有效性。

3.6 对比结果

为了更直观地体现本文模型的优势，将本文模型与中心频率法VMD-KPCA-BP模型及WOA-VMD-BP模型测试集的诊断准确率进行对比，结果如表3所示。由表3可知，本文提出的WOA-VMD-KPCA-BP模型在故障诊断过程中得到了更高的诊断准确率，取得了更显著的效果，可为后续的研究及应用提供参考。

表3 不同模型对应的诊断准确率 (%)

模型

诊断率

WOA-VMD-KPCA-BP

中心频率法VMD-KPCA-BP

WOA-VMD-BP

90.67

4 结论

本文提出了一种将基于综合评价指标的VMD参数寻优、KPCA特征融合和BP网络相结合的齿轮故障诊断方法，并用实例进行了分析和验证。

（1）提出构建基于包络熵与峭度的综合评价指标并采用WOA算法对VMD参数进行寻优。

（2）提出对不同状态下最优的K和α取平均值，最终得到对任何状态下都适用的最优参数。用最优参数进行VMD分解后再利用同样的综合评价指标筛选出最优IMF分量，提取多域高维特征后经过KPCA模型完成特征的融合，最后导入BP网络中进行故障诊断。

通过对比分析，中心频率法VMD-KPCA-BP模型的准确率和WOA-VMD-BP模型的准确率分别为90.67%及94%，而本文所提出方法的诊断准确率为98%。因此可以证明本文所述方法能更有效地提取特征向量，且具有更高的诊断准确率，更适用于齿轮的故障诊断。

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Chen H Z， Wang J X， Tang B P，et al.An integrated approach to planetary gearbox fault diagnosis using deep belief networks［J］.Measurement Science and Technology，2017，28（2）：025010.

2	刘鲲鹏，白云川，吕麒鹏，等.基于改进傅里叶变换的滚动轴承故障诊断［J］.内燃机与配件，2018（19）：56-57.

3	文成，周传德.基于灰色关联度的形态滤波及滚动轴承故障诊断中应用［J］.振动与冲击，2015，34（14）：51-55.

4	杨超，杨晓霞.基于灰色关联度和Teager能量算子的轴承早期故障诊断［J］.振动与冲击，2020，39（13）：224-229.

5	涂志松.基于小波包和支持向量机的滚动轴承故障诊断［J］.机电工程技术，2020，49（12）：208-211.

6	张琛，郭俊超，甄冬，等.基于小波包时延相关解调的滚动轴承故障诊断方法［J］.机械设计，2020，37（6）：24-28.

7	戚晓利，叶绪丹，蔡江林，等.基于变分模态分解与流形学习的滚动轴承故障特征提取方法［J］.振动与冲击，2018，37（23）：133-140.

8	Dragomiretskiy K， Zosso D.Variational mode decomposition［J］.IEEE Transactions on Signal Processing，2014，62（3）：531-544.

9	武英杰，甄成刚，刘长良.变分模态分解在风电机组故障诊断中的应用［J］.机械传动，2015，39（10）：129-132.

10	徐甜甜，孙文磊，王宏伟，等.变分模态分解与谱峭度法在齿轮箱故障诊断中的应用［J］.机械科学与技术，2020，39（6）：873-878.

11	Zhang Y G， Li R X， Zhang J H.Optimization scheme of wind energy prediction based on artificial intelligence［J］.Environmental Science and Pollution Research，2021，28（29）：39966-39981.

12	刘秀丽，徐小力，吴国新，等.基于变分模态分解的故障弱信息提取方法［J］.华中科技大学学报（自然科学版），2020，48（7）：117-121.

13	张萍，张文海，赵新贺，等.WOA-VMD算法在轴承故障诊断中的应用［J］.噪声与振动控制，2021，41（4）：86-93，275.

14	Mirjalili S， Lewis A.The whale optimization algorithm［J］.Advances in Engineering Software，2016，95（3）：51-67.

15	尚晓三，王式成，王振龙，等.基于样本熵理论的自适应小波消噪分析方法［J］.水科学进展，2011，22（2）：182-188.

16	Vinay A， Shekhar V S， Murthy K，et al.Face recognition using gabor wavelet features with PCA and KPCA-A comparative study［J］.Procedia Computer Science，2015，57（12）：650-659.

17	陈东宁，张运东，姚成玉，等.基于变分模态分解和多尺度排列熵的故障诊断［J］.计算机集成制造系统，2017，23（12）：2604-2612.

Options

Outlines

模态框（Modal）标题

Abstract

Cite this article

1 基于综合评价指标的VMD参数优化

1.1 VMD算法原理

1.2 综合评价指标及适应度函数

1.3 基于WOA的VMD参数优化流程

图1 基于WOA优化VMD参数流程图

2 基于KPCA与BP网络的故障诊断方法

2.1 IMF分量筛选及特征提取

2.2 基于KPCA的特征融合模型构建

2.3 基于BP网络的故障诊断模型构建

图2 故障诊断BP网络结构图

2.4 故障诊断流程

3 实例验证

3.1 原始数据

图3 QPZZ-II旋转机械故障模拟试验台

3.2 WOA优化VMD

图4 随迭代次数的最优个体适应度值变化曲线

表1 不同状态下得到的最优VMD参数

3.3 KPCA特征融合

表2 正常状态下前3个样本各IMF分量的适应度值

图5 主元累积贡献率分布图

图6 WOA-VMD-KPCA特征分布图

3.4 BP网络诊断

图7 本文方法（WOA-VMD-KPCA-BP）诊断结果图

3.5 对比试验

图8 中心频率法VMD-KPCA特征分布图

图9 中心频率法VMD-KPCA-BP模型诊断结果图

图10 WOA-VMD-BP模型诊断结果图

3.6 对比结果

表3 不同模型对应的诊断准确率 (%)

4 结论

References