Journal of Shenyang Aerospace University >

2024 , Vol. 41 >Issue 4: 32 - 40

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.04.004

Mechanical and Materials Engineering

Stiffness identification of joint surface by considering the influence of uneven action range of bolt preload

  • Wujiu PAN ,
  • Hongxing SONG ,
  • Xianmu LI
Expand
  • College of Mechatronics Engineering，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2024-03-18

  Online published: 2024-09-10

Fold

Abstract

The changes in stiffness and damping of the bolted joint surface can cause the changes of dynamic characteristics of the whole bolted joint structure，so it is of great practical value to accurately obtain the dynamic parameters of the joint surface in engineering.Based on the bolted structure，an improved equivalent model of the stiffness of the joint surface with uneven distribution in the range of bolt preload was proposed，and the distribution of different stiffness matrix elements in the finite element modeling was analyzed.The stiffness parameter identification of bolted joint surface was carried out by combining experiment and finite element analysis method.The results show that the increase of the number of stiffness matrix elements can improve the accuracy of natural frequency solutions to some extent.At the same time，considering the uneven stiffness distribution of the joint surface in the range of bolt preload，the equivalent modeling accuracy of the bolted joint structure can be effectively improved.

Key words： bolted joint; joint surface; range of bolt preload application; stiffness matrix elements; parameter identification

Cite this article

Wujiu PAN , Hongxing SONG , Xianmu LI . Stiffness identification of joint surface by considering the influence of uneven action range of bolt preload[J]. Journal of Shenyang Aerospace University, 2024 , 41(4) : 32 -40 . DOI: 10.3969/j.issn.2095-1248.2024.04.004

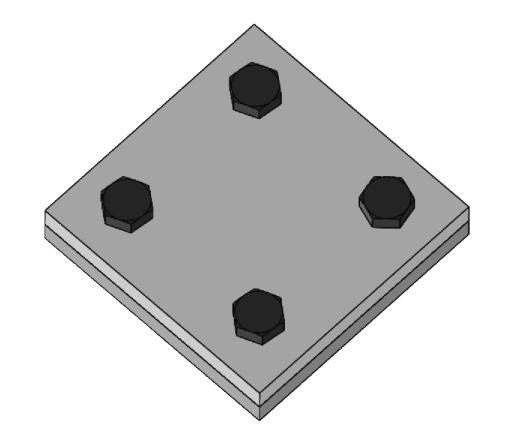
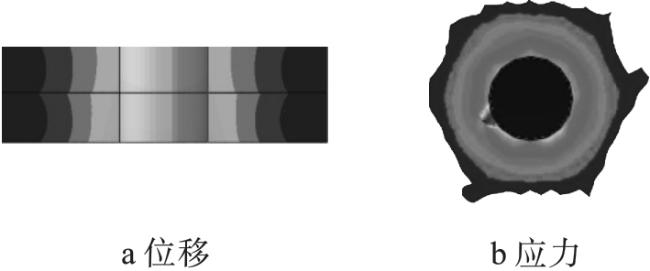
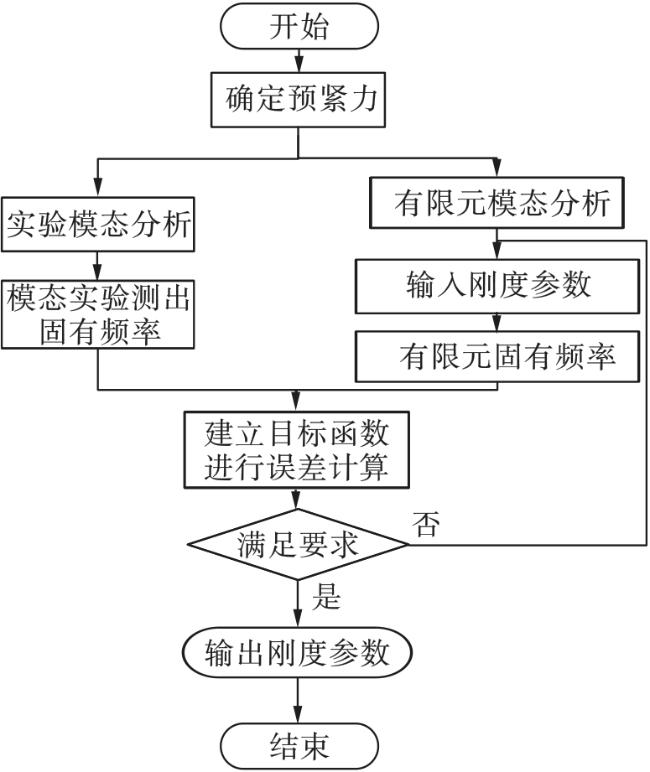
大型的机械设备由各种零部件构成，零部件之间相互接触的表面被称为结合面。结合面的产生使得机械系统产生非连续性，机械系统的性能发生改变。结合面在复杂的载荷作用下，表现出既有刚度又有阻尼的动态特性，从而显著影响机械结构的整体动态特性，使得机械结构的整体动态特性更为复杂［1］。研究表明，结合面的刚度通常是整个机械结构刚度的重要组成部分，结合面的接触刚度可以占总刚度的60%~80%［2］。机械结合面动态特性的影响因素众多，作用机理复杂。螺栓连接是机械结构中最常见、应用最广泛的连接方式，所以对螺栓连接结合面的研究具有重要的意义。螺栓连接结合面的接触特性除了受到接触面自身特性，如材料弹性模量、接触面表面粗糙度等影响外，螺栓的数量［3］、位置［4］、预紧力的大小［5］、顺序［6-7］对结合面的动态特性也有显著影响［8-9］。螺栓连接结合面的动态参数不易在实验中测出，所以一般采用实验与有限元分析软件相结合的方法识别结合面的动态参数。
很多研究人员对结合面动态参数的研究主要通过实验法直接测量连接结构中被连接件的力与变形，并通过力与变形之间的关系曲线获取结合面的动态参数［10-12］。实验法具有明确的物理意义，但是结合面变形量一般为微米级，测量过程中容易产生较大误差，从而影响实验精度。考虑实验法的不足，基于频响函数的结合面动态参数辨识方法［13-15］应运而生。该方法采用子结构方法建立含有柔性连接特性的动力学矩阵方程，方程中的矩阵从频响实验获取的频响函数中得到，将结合面动态参数辨识的问题转化为动力学矩阵求解的问题，从而反推结合面动态特性参数。随着研究的深入，很多研究人员发现模态参数作为结构固有特性之一，不受结构阻尼影响，具有实验测试方法成熟、信噪比高、数据准确可靠等优点，广泛应用于各个领域。通过模态实验得到试件的固有频率及对应阶次的模态振型，并以此作为有限元模型的评价指标。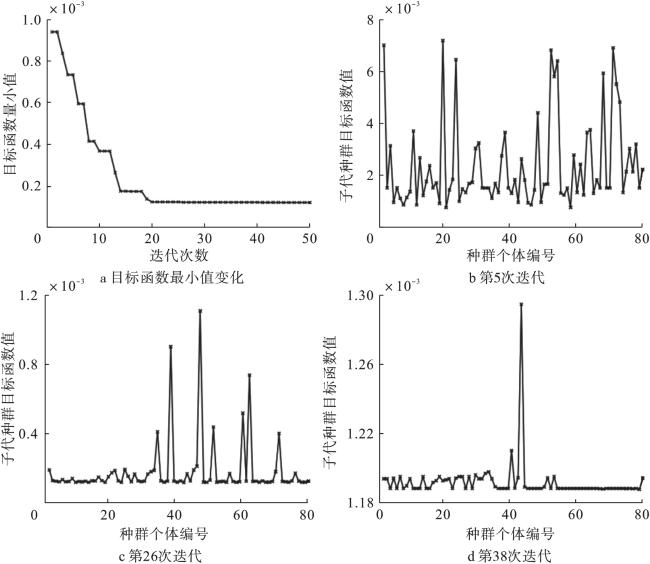通过有限元模型修正的方法对结合面刚度参数进行修正与优化［16-18］，使有限元仿真模型的固有频率和振型与模态实验结果的误差保持在可接受的范围内，即认为有限元仿真模型中结合面刚度参数与实际相符。
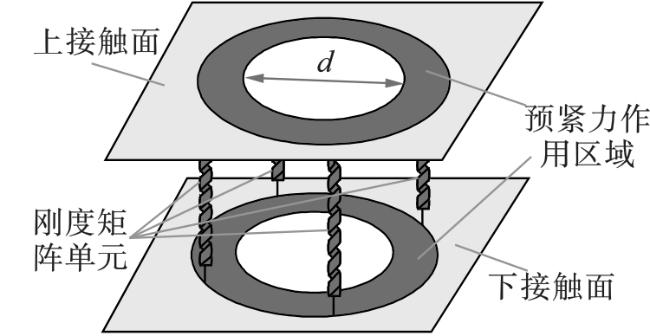
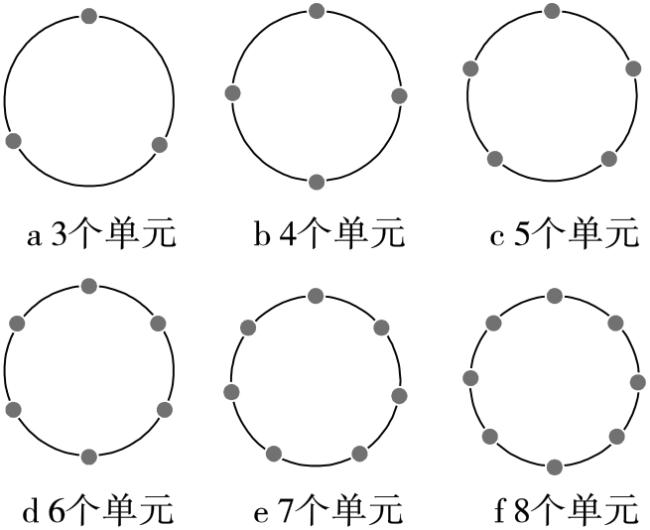
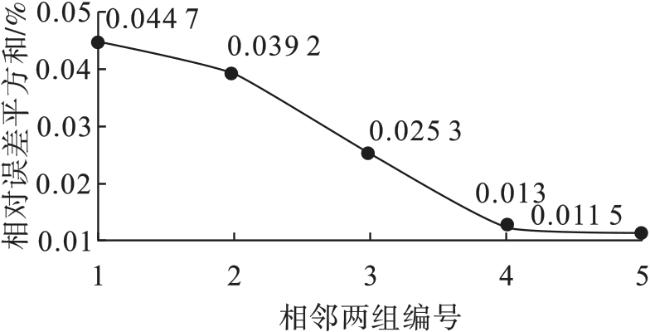
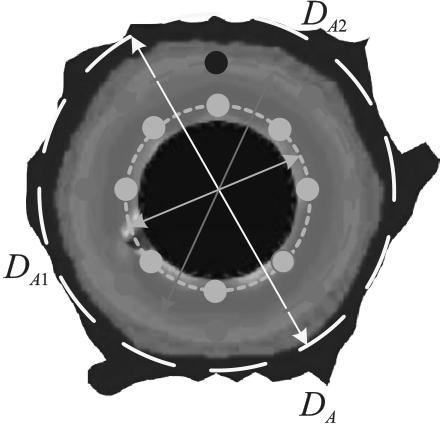
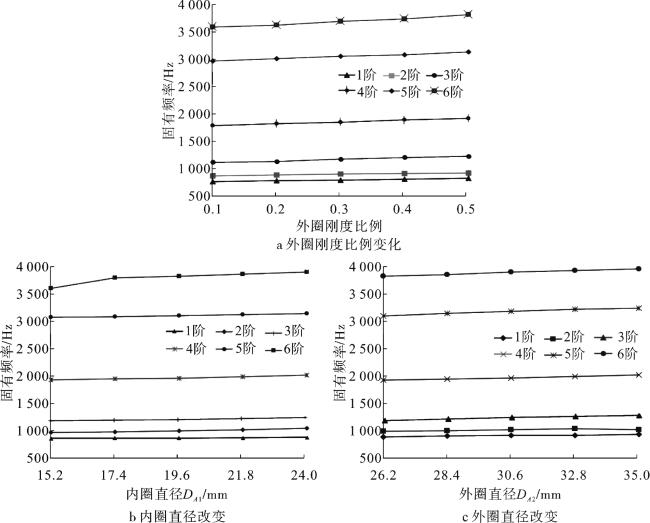
从以上对螺栓弹性相互作用及求解结合面刚度参数的文献中可以看出，研究中没有考虑到实际螺栓连接结构中螺栓作用范围不均进而影响求解结合面刚度参数的问题。因而本文的主要研究内容为：（1）在考虑螺栓预紧力作用范围内刚度分布不均情况的基础上，提出双层刚度矩阵单元分布模型；（2）分析了刚度矩阵单元的数量、等效压力圆直径及刚度参数分配比例对建模精度的影响。

1 结合面建模

分析刚度矩阵单元数量对模型精度的影响，同时考虑螺栓预紧力作用范围内结合面刚度分布不均，从而提出建立双层刚度矩阵单元模型，以此来提高等效建模的准确性。
图1为螺栓连接结构，其中被连接件长为252 mm，宽为224 mm，厚度为16 mm，两个螺栓孔间距分别为126 mm和112 mm，采用4个8.8级的M24×55的外六角螺栓连接，初始预紧力为30 kN。
图1 螺栓连接结构模型

1.1 结合面建模刚度单元的数量与分布

传统建模方法中接触部分的刚度为螺栓刚度和结合面刚度共同作用的结果，且没有考虑螺栓连接结构结合面上刚度分布不均的因素，所以与真实的结合面接触特性存在较大误差。将螺栓刚度和结合面刚度分别进行等效建模，同时考虑到螺栓预紧力作用范围内结合面刚度分布不均，可以提高结合面等效模型的精度，从而提高结合面刚度参数的辨识精度。在对结合面进行等效建模时，只在螺栓作用范围内对两个被连接件的节点使用刚度矩阵单元连接，其他部分不连接，如图2所示。
图2 螺栓预紧力作用区域
本文假设结合面等效法向总刚度 K n = 8.75 × 10 9 N / m，等效切向总刚度 K τ = 7.56 × 10 8 N / m。分别在等效压力圆上均匀设置3~8个节点施加MATRIX27刚度矩阵单元，如图3所示，并将等效刚度均匀分配给每个MATRIX27矩阵单元，每个矩阵单元具体参数如表1所示。
图3 不同数量刚度矩阵单元分布
表1 结合面等效刚度分配结果
刚度单元数量 法向 K n / 10 9 切向 K τ / 10 8
3 2.92 2.52
4 2.19 1.89
5 1.75 1.51
6 1.46 1.26
7 1.25 1.08
8 1.09 0.95
根据表1中数据设置MATRIX27刚度矩阵单元参数，并进行有限元模态仿真分析，结果如表2所示。
表2 有限元模态仿真结果 (Hz)
刚度矩阵数量 模态频率
第一阶 第二阶 第三阶 第四阶 第五阶 第六阶
3 851.17 959.84 1 197.58 1 875.50 3 046.03 3 662.50
4 860.55 970.97 1 210.44 1 894.16 3 071.16 3 684.62
5 871.68 979.18 1 219.83 1 907.28 3 085.20 3 706.16
6 877.41 987.11 1 230.07 1 920.68 3 097.86 3 718.80
7 882.60 991.42 1 237.61 1 929.73 3 106.77 3 730.23
8 887.45 996.57 1 244.02 1 938.95 3 112.96 3 738.84
根据式（1）计算表2中每两个相邻仿真组结果之间的固有频率相对误差平方和，得到的结果如表3及图4所示。
G i = ∑ j = 1 6 f j k + 1 - f j k f j k + 1 2
式中： f j k + 1和 f j k分别为第k+1、k次仿真中第j阶固有频率。
表3 相邻仿真组固有频率相对误差平方和 (%)
组号 相对误差平方和
1 0.044 0
2 0.039 2
3 0.025 3
4 0.013 0
5 0.011 5
图4 相邻仿真结果固有频率相对误差平方和变化趋势
根据表3以及图4的结果可知，随着等效压力圆上刚度矩阵单元数量的增加，有限元模态仿真得到的固有频率值的波动越来越小。说明在一定程度上，增加刚度矩阵单元可以提高固有频率解的精度，但是过多的刚度矩阵单元对固有频率解精度的提高影响不大，所以综合考虑计算精度与计算效率，在等效压力圆上使用8个刚度矩阵单元。

1.2 单层和双层刚度矩阵单元分布模型

根据吉村允孝思想，当结合面条件一定，结合面的平均接触压力相同时，结合面单位面积的等效刚度相同。由于螺栓预紧力作用范围是有限的，所以假设螺栓预紧力作用范围内结合面刚度符合吉村允孝思想，结合面各处的单位面积等效刚度相同，即螺栓预紧力作用范围内结合面刚度是均匀分布的。所以螺栓预紧力作用范围内结合面刚度为
K n = k n S A
K τ = k τ S A
式中： S A为等效压力圆面积； k n和 k τ分别为结合面单位面积法向和切向刚度。
假设结合面等效法向总刚度 K n = 8.75 × 10 9 N / m，等效切向总刚度 K τ = 7.56 × 10 8 N / m。设定等效压力圆直径DA 为 1.5   d w ∼ 2.0   d w，并在等效压力圆上设置8个节点施加MATRIX27刚度矩阵单元用以连接两个被连接件，进行有限元模态求解，得到模态参数如表4所示。
表4 有限元模态仿真结果 (Hz)
等效压力圆直径 模态频率
第1阶 第2阶 第3阶 第4阶 第5阶 第6阶
1.5dw 869.42 980.46 1 233.03 1 933.54 3 069.24 3 677.49
1.6dw 872.80 997.17 1 230.77 1 930.31 3 091.22 3 688.71
1.7dw 873.67 986.28 1 242.75 1 926.96 3 092.40 3 702.60
1.8dw 877.18 993.43 1 238.13 1 935.05 3 102.55 3 719.73
1.9dw 882.73 998.75 1 250.92 1 941.77 3 110.64 3 710.84
2.0dw 887.45 996.57 1 244.02 1 938.95 3 112.96 3 738.84
根据表4可以看出，等效压力圆直径越大，各阶固有频率值越大，说明螺栓连接结构越稳定，并且模态阶次越高，等效压力圆直径对模态固有频率影响越大，所以合理选择等效压力圆直径是必要的。
通过对螺栓连接结构进行有限元静力学分析可得位移和应力，结果如图5所示。由图5可以看出，螺栓预紧力作用范围内，应力和位移不是均匀分布的，距离螺栓孔距离越远的地方应力和位移越小。所以结合面刚度分布也是不均匀的，这与单层刚度矩阵单元模型的假设是矛盾的。所以，提出双层刚度矩阵单元分布的模型对螺栓连接结合面进行等效建模，在预紧力作用范围内建立双层刚度矩阵单元分布的模型以提高刚度辨识的精度。
图5 位移及应力图
同样假设结合面等效法向总刚度 K n = 8.75 × 10 9 N / m，等效切向总刚度 K τ = 7.56 × 10 8 N / m。建立如图6所示的双层刚度矩阵单元分布模型，其中内等效压力圆直径为DA 1，外等效压力圆直径为DA 2，分别在两等效压力圆上均匀设置8个节点施加MATRIX27刚度矩阵单元用以连接两个被连接件上的对应节点，进行有限元模态分析。
图6 双层刚度矩阵单元分布模型
根据图7可以看出，当内外等效压力圆上刚度矩阵参数比例不变时，等效压力圆直径越大，固有频率值越高，且阶次越高变化率越大。内等效压力圆直径变化比外等效压力圆直径变化对固有频率的影响更明显。同时，当等效压力圆直径一定时，内外两等效压力圆上刚度矩阵单元的刚度分配比例对固有频率也有影响，其中外圈刚度矩阵单元上刚度分配比例越高，固有频率值越大，说明外等效压力圆上刚度矩阵单元刚度参数比例越大，螺栓连接结构越稳定。
图7 等效压力圆对固有频率的影响

2 结合面刚度参数的逆向识别

2.1 模态实验

使用东华测试DH5922D动态信号测试分析系统（如图8所示）对螺栓连接结构进行自由模态实验，获取螺栓连接结构的固有频率为结合面动态参数辨识提供实验数据及基础。如图8所示，采用弹性绳将螺栓连接结构试件进行悬挂，模拟自由边界。弹性绳的刚度和阻尼较小，对螺栓连接结构模态实验结果的影响可以忽略不计。采用加速度传感器采集振动信号并通过数据采集仪传输到计算机中的振动测试分析平台进行处理，采用Polymax算法对模态实验参数进行识别。
图8 东华测试模态实验系统
根据螺栓连接板试件的结构特点，进行尺寸的划分与实验测点的布置，最终建立如图9所示的16测点几何模型，其中，响应点加速度传感器布置在被连接件中心的C1点。采用移动力锤的方法，分别对每一个测试点进行5次敲击以减小误差，共得到16组频响函数。
图9 测点及响应点布置
选择常用的模态置信准则（modal assu-rance criterion，MAC）来对实验数据的可信度进行检查。模态置信准则是一种用于检查各阶模态振型向量之间正交性的数学工具，与系统矩阵无关。模态置信矩阵及其MAC柱状图是关于主对角线对称的，主对角线上为各振型向量与自身的估计结果，所以其值都为100%。模态置信矩阵的行号与列号分别表示两阶模态，矩阵元素的大小则代表了两阶模态振型向量的估计结果，其值越接近于0，说明模态实验结果越可信。一般情况下，非对角线上矩阵元素的MAC值只要不超过20%，即可认定此次实验所获取的模态参数是准确的。
如表5所示，本次实验的MAC最大值为8.2%，表明通过模态实验选取的六阶模态之间具有很好的正交性，验证了模态实验得到的模态参数的可靠性。MAC柱状图如图10所示。
表5 模态置信矩阵
阶次 1 2 3 4 5 6
1 1 0.012 0.006 0.007 0.082 0.007
2 0.012 1 0.081 0.043 0.018 0.015
3 0.006 0.081 1 0.073 0.002 0.061
4 0.007 0.043 0.073 1 0.053 0.036
5 0.082 0.018 0.002 0.053 1 0.015
6 0.007 0.015 0.061 0.036 0.015 1

2.2 刚度参数辨识流程

结合面刚度参数识别流程如图11所示。本文以仿真固有频率和实验固有频率之间的差值最小化构建目标函数计算模型，其表达式为
m i n γ K n , K τ 1 , K τ 2 = ∑ i = 1 6 f i F E - f i T / f i T 2 K L ≤ K j ≤ K U
式中： f i F E和 f i T分别为第 i阶模态固有频率的有限元仿真值和模态试验值；KL 和KU 分别为设计变量的下限和上限。
图11 结合面刚度参数识别流程图

3 结果与验证

3.1 刚度参数辨识结果

根据遗传算法的流程对螺栓初始预紧力为30 kN的螺栓连接结合面进行刚度参数辨识，每一次迭代的目标函数平均值最小值的变化如图12a所示，部分迭代次数的目标函数值如图12b、12c、12d所示。根据图12可以看出，当遗传算法迭代至第20代时目标函数已经收敛。
图12 种群迭代目标函数值变化

3.2 辨识结果验证

通过实验与有限元分析相结合的方法对螺栓连接结构进行刚度参数辨识，得到的每个刚度矩阵单元的法向刚度 k n = 3.164 × 10 9 N / m，x方向切向刚度 k τ x = 1.281 × 10 8，y方向切向刚度为 k τ y = 1.605 × 10 8 N / m。以此计算得到结合面等效法向总刚度 k n = 2.531 × 10 10 N / m，x方向等效切向总刚度为 k x = 1.025 × 10 9 N / m，y方向等效切向总刚度为 k y = 1.284 × 10 9 N / m。将辨识的结合面刚度结果输入有限元仿真模型中进行模态分析，获得的固有频率值如表6所示，与模态实验得到的固有频率值进行误差分析。固有频率值的误差在可接受的范围内，所以认为辨识得到的结合面刚度参数是有效的。
表6 参数优化后有限元仿真与模态试验固有频率值
阶次 固有频率/Hz 误差/%
模态实验 识别后仿真
第一阶 855.36 873.37 2.1
第二阶 967.86 997.72 3.1
第三阶 1 283.64 1 238.81 -3.5
第四阶 1 989.38 1 926.56 -3.1
第五阶 2 964.68 3 087.41 4.1
第六阶 3 610.60 3 736.64 3.4

3.3 单、双层刚度矩阵单元辨识结果分析

分别对单层刚度矩阵单元模型和双层刚度矩阵单元模型进行结合面刚度参数进行辨识，有限元模态仿真结果如表7所示。
表7 不同模型固有频率比较 (Hz)
阶次 固有频率
模态实验 双层刚度单元分布 与模态实验误差 单层刚度单元分布 与模态实验误差
第一阶 855.36 873.37 18.01 878.64 23.28
第二阶 967.86 997.72 29.86 1 004.82 36.96
第三阶 1 283.64 1 238.81 -44.83 1 233.62 -50.02
第四阶 1 989.38 1 926.56 -62.82 1 917.90 -69.48
第五阶 2 964.68 3 087.41 122.73 3 099.47 134.99
第六阶 3 610.60 3 736.64 126.04 3 750.51 139.91
根据表7可以看出，双层刚度矩阵单元分布模型的固有频率与单层刚度矩阵单元分布的模型固有频率与模态实验之间误差虽然都在合理范围之内，但是双层刚度矩阵单元与模态实验之间的误差值更小。所以在一些要求更精细的模型中使用改进的双层刚度矩阵单元分布模型对结合面刚度的辨识会更加准确。

4 结论

本文以螺栓连接的模型为研究对象，在考虑螺栓预紧力作用范围内结合面刚度分布不均的基础上采用实验与有限元分析相结合的方法对结合面刚度参数进行辨识。
（1） 通过对螺栓连接结构静力学分析得出，螺栓预紧力对被连接件产生的应力和位移只在螺栓孔附近的一定圆形区域内产生。同时螺栓预紧力作用范围内结合面刚度分布随着径向距离的增大而减小。
（2） 在一定程度上，增加刚度矩阵单元可以提高固有频率解的精度，但是过多的刚度矩阵单元对固有频率解精度的提高影响不大，所以综合考虑计算精度与计算效率，在等效压力圆上使用8个刚度矩阵单元。
（3） 基于优化算法的实验与有限元分析相结合的螺栓连接结合面刚度参数辨识方法可以准确且便捷地得到结合面刚度参数。考虑螺栓预紧力范围内结合面刚度分布不均的有限元等效模型可以提高建模精度，从而提高结合面刚度参数的辨识精度。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
胡兆稳，刘焜，王伟，等.粗糙表面接触模型的研究现状和展望［J］.低温与超导，2011，39（12）：71-74.

2
Burdekin M， Back N， Cowley A.Analys is of the local deformations in machine joints［J］.Journal of Mechanical Engineering Science，1979，34（3）：15-17.

3
Pan W J， Li X Y， Sun L，et al.General prediction model of residual pretightening force of bolt group with one-step and multi-step pretightening and analysis of influencing factors from the perspective of elastic interaction［J］.Engineering Computations，2023，40（4）：1-36.

4
Matsubara D， Teranishi M， Wakashima Y.Elastic interaction in multiple bolted timber joints［J］.Journal of Wood Science，2022，68（1）：1-11.

5
Campen D H V.A systematic bolt-tightening procedure for reactor vessel flanges［J］.Journal of Pressure Vessel Technology，2003，457（11）：9-16.

6
Huang H， Wang Y， Wei T，et al.Study of preload relaxation and optimization of wind turbine bolted connections based on the improved elastic interaction coefficient method［J］.Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，2023，237（8）：1194-1206.

7
Abid M， Hussain S.Relaxation behaviour of gasketed joints during assembly using finite element analysis［J］.Sadhana：Academy Proceedings in Engineering Science，2010，35（1）：31-43.

8
Pan W J， Li X P， Wang L L，et al.Influence of contact stiffness of joint surfaces on oscillation system based on the fractal theory［J］.Archive of Applied Mechanics，2018，88（4）：525-541.

9
Pan W J， Li X P， Wang L L，et al.A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification［J］.European Journal of Mechanics A：Solids，2017，66（2）：94-102.

10
Eriten M， Lee C H， Polycarpou A A.Measurements of tangential stiffness and damping of mechanical joints：direct versus indirect contact resonance methods［J］.Tribology International，2012，50：35-44.

11
蔡力钢，郝宇，郭铁能，等.螺栓结合面法向静态刚度特性提取方法研究［J］.振动与冲击，2014，33（16）：18-23.

12
王世军，赵金娟，张慧军，等.一种结合部法向刚度的预估方法［J］.机械工程学报，2011，47（21）：111-115，122.

13
Okubo N， Miyazaki M.Development of uncoupling technique and its application［C］//Proceedings of International Modal Analysis Conference.Orlando：ASME，1984：1194-1200.

14
王威，胡于进，凌玲.考虑连接特性的子结构频响综合方法及实现［J］.中国机械工程，2013，24（10）：1385-1389.

15
李玲，蔡安江，阮晓光，等.栓接结合部刚度建模与特性分析［J］.振动工程学报，2017，30（1）：1-8.

16
Tlusty J， Ismail F.Dynamic structural identification tasks and methods［J］.CIRP Annals Manufacturing Technology，1980，29（1）：251-255.

17
Thekkepat A A， Devadula S， Law M.Identifying joint dynamics in bolted cantilevered systems under varying tightening torques and torsional excitations［J］.Journal of Vibration Engineering & Technologies，2022，10（2）：459-469.

18
Liu Y， Wang M， Gao X.An investigation of dam-ping mechanism in two-layered beam with general sectional shape［J］.Journal of Vibration Enginee-ring & Technologies，2019（7）：179-188.

Options
Outlines

/

〈 〉

Website Copyright © Editorial Department of Journal of Shenyang Aerospace University
Tel: 024-89723779　
Fax: 024-89723779　
E-mail: shxbok@163.com
Powered by Beijing Magtech Co. Ltd