在飞行器研制过程中，虽然目前的表面加工工艺已经能够保证较低的粗糙度水平［1-2］，但由于机翼、叶片等部件的工作环境复杂多变，在使用和维护过程中其表面容易出现微小冰晶/沙尘/污垢堆积、漆皮剥落和腐蚀等情况，导致运行状态偏离设计状态，造成层流边界层转捩显著提前、湍流边界层厚度增大，影响飞行器的气动特性。与光滑表面相比，粗糙壁面不但会导致机翼阻力增大，还增加了边界层下游分离的可能性，使层流等外形设计的收益降低［3-4］，特别是对注重飞行效率的小型通用航空飞行器影响更大。日本本田公司研制的HondaJet高速公务机采用了大量层流设计技术，为避免喷漆等非设计因素的干扰，还专门研发了一套精细化喷漆工艺和配套专用车间［5］。但由于粗糙度的影响未形成广泛的定量认识，使用中的壁面粗糙状态亦存在不确定性，目前基于计算流体力学（computational fluid dynamics，CFD）的气动设计工程应用大都是面向光滑壁面开展的［6］。另一个重要限制因素是，现有的雷诺平均N-S（Reynolds-averaged navier-stocks，RANS）湍流和转捩模型基本都是基于光滑壁面假设发展的［7-9］，虽然提出较多修正模型，但由于不同粗糙分布的影响规律较为复杂，精细化、工程化的粗糙壁面流动实验并不易开展，导致粗糙壁面边界层流动模拟方法的可信度还没有得到广泛的验证和认可。
粗糙壁面按粗糙元分布情况的不同可分为离散式和分布式两类。从飞行器使用角度看，均匀分布式粗糙元更为常见，且粗糙壁面实验也常以黏贴砂纸的方式进行，因此本文以均匀分布式粗糙壁面作为研究对象。从流动模拟角度出发，对均匀分布的微小粗糙元直接进行几何建模和网格生成是不现实的，因此需要通过物理模型引入粗糙度的影响。根据湍流边界层分层结构，可以通过粗糙壁面函数来调整对数律［10］。ANSYS FLUENT软件［11］即采用这种方式，并针对网格相关性进行了修正处理。但这种壁面函数方法只适用于附着流动，同时对匹配点的选择非常敏感［8］。另一种思路则是对RANS湍流/转捩模型进行修正。Schlichting等［12］和Ligrani等［13］在粗糙壁面流动方面进行了大量的实验研究，得到了粗糙度影响下的湍流边界层壁面律表达，成为粗糙壁面边界层研究及模型修正的基础。
围绕工程常用的湍流模型，Aupoix等［14］介绍了由法国宇航院（ONERA）和美国波音公司针对Spalart-Allmaras（S-A）湍流模型［7］提出的粗糙壁面流动修正方法。针对k-ω湍流模型，Wilcox［8］利用Schlichting等［12］的结论提出了不同粗糙元高度下的ω边界条件。Hellsten等［10］针对k-ω 切应力输运（shear stress transport，SST）湍流模型［9］也提出了相应的关联函数表达。Knopp等［15］指出了Wilcox粗糙壁面边界条件在网格和收敛性方面的不足，并提出了同时修改湍动能和耗散率边界条件的改进方案。刘通等［16］以边界层速度亏损量为指标对该模型的经验参数进行了重新标定。但现有研究中对于不同粗糙壁面修正模型的性能对比研究较少，且算例多以平板为主，对评价不同粗糙壁面修正模型的可信度及工程应用中的选用缺乏指导意义。
对于粗糙壁面诱导的边界层转捩，许多学者基于RANS方法，尤其是间歇因子类建模方法进行了相关研究。Stripf等［17］将离散粗糙单元模型与双层k-ε模型相结合构造了粗糙壁面湍流边界层模型，并引入粗糙壁面动量厚度雷诺数作为转捩触发判据，间歇因子作为转捩区模型，构造了当地化的转捩预测方法，后续还进一步进行了拓展［18］。Lorenz等［19］在此基础上构建了新的粗糙壁面诱导bypass转捩预测准则。目前，以Langtry等［20］提出的γ-Reθt 转捩模型为代表的基于当地化经验关系式的转捩建模方法应用广泛。如何将已有研究成果引入γ-Reθt 转捩模型及与已有湍流模型粗糙壁面修正相耦合都是值得讨论的问题。
1 粗糙壁面边界层流动建模
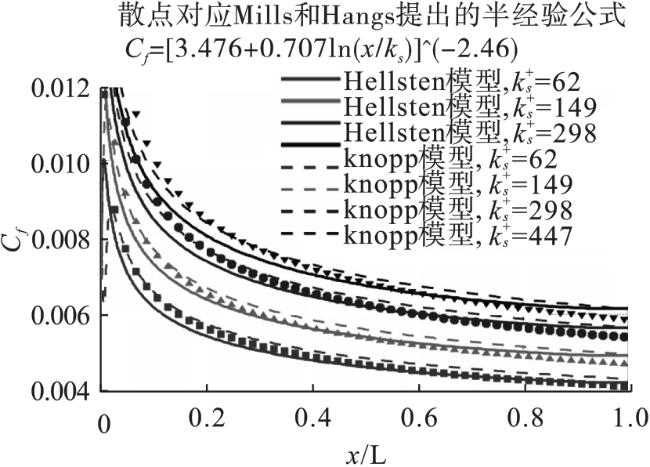
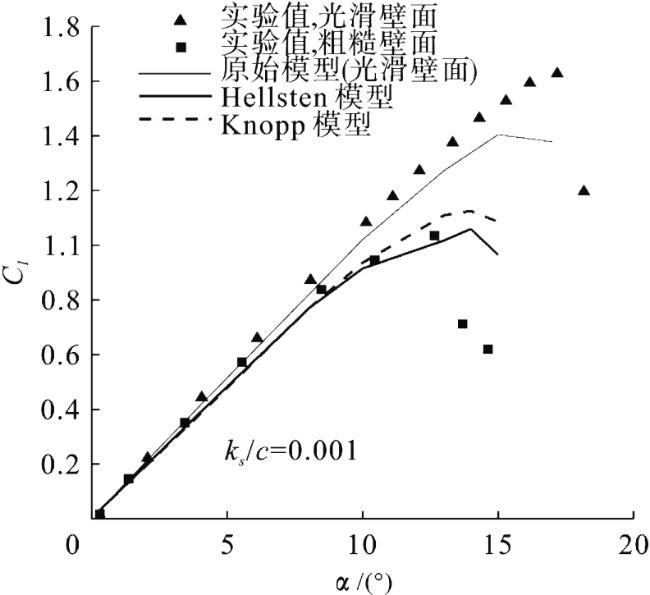
对于微小粗糙元均匀分布的粗糙壁面，若不考虑粗糙元形状而只考虑平均（等效）高度ks 的影响，则可以采用湍流边界层内层中的黏性长度尺度ν/uτ 对ks 进行无量纲化［21］，其中：uτ =（τw /ρ）1/2为壁面摩擦速度；ν为运动黏性系数；τw 为壁面切应力。得到的无量纲等效粗糙元高度ks +=ks ·uτ /ν与距壁面的无量纲高度y +的意义类似，可以用来描述壁面粗糙度水平。根据ks +对湍流边界层速度剖面的不同影响，Schlich-ting等［12］将粗糙壁面大致分为水力学光滑壁面（hydraulically smooth surface，ks + ≤5）、过渡粗糙壁面（transitionally rough surface，5＜ks + ≤70）和完全粗糙壁面（fully rough surface，ks + ＞70）三类。上述两个阈值也有不同的提法，例如Ligrani等［13］采用的是2.25和90。实验表明，当粗糙度非常小时，粗糙元被淹没在黏性底层之内，不会对边界层流动造成大的影响，黏性底层仍然存在；随着ks + 的增大，流动成为完全粗糙流，黏性底层将消失［21］，壁面处的雷诺应力不再为0（对于RANS方法即涡黏性系数不为0）。
1.1 粗糙壁面湍流模型修正
k-ω SST湍流模型［9］将k-ω和k-ε模型相融合，在边界层内外通过开关函数进行切换，并将Bradshaw假设引入涡黏性系数的定义中，得到了广泛的发展和应用。由于原始k-ω SST模型的ω物面边界条件 与黏性有关，如式（1） 所示。
式中：Δy为壁面法向首层网格高度；νw 为壁面附近的黏性系数，因此可以采用边界层内层特征速度uτ 和黏性长度尺度ν/uτ 定义［21］，根据量纲分析有ωw ~uτ 2 /ν。若将壁面 值与粗糙元高度ks +相关联，新的壁面 值可表示为
式中：S rough为ks +的关联函数，根据粗糙度对边界层的影响，两者应成反比关系：当S rough→∞时（ks +很小），ωw →∞，此时式（2） 与原始物面边界条件式（1） 是一致的；而当S rough→0时（ks +很大），ωw 为有限值，以此驱动雷诺应力的生成。
1.1.1 比耗散率边界条件修正模型
Hellsten等［10］提出的关联关系为
式中：a 1=0.31为Bradshaw假设常数；S为应变不变量；F 2为原始k-ω SST湍流模型［9］的开关函数；y为距离壁面的高度。而湍动能k的物面边界条件仍保持原始k-ω SST湍流模型的设定，即kw =0。
1.1.2 湍动能和比耗散率边界条件修正模型
其中
式中：模型常数β *=0.09；卡门常数κ=0.41。
1.1.3 程序实现
国家数值风洞风雷软件［22］是由中国空气动力研究与发展中心面向全国发布的混合CFD计算开源平台，采用面向对象的大型软件设计理念，利用C++语言编写程序，具有良好的通用性和可扩展性。本文对风雷软件的修改主要集中在湍流结构网格求解器TurbSolverStruct中，即所有修改暂时只针对结构网格。参照风雷手册对公式进行无量纲化，例如修改k-ω SST湍流模型的比耗散率ω的边界条件，无量纲形式为
参考k-ω SST模型混合函数F 2的构造方式在程序中加入新的开关函数F 3，来实现粗糙壁面湍流模拟。
1.1.4 算例确认与参数校核
1.2 粗糙壁面边界层转捩模拟
当边界层动量厚度雷诺数Reθ 随流动增长到一个临界值Reθt 时，边界层转捩就会发生，这是转捩模型构造的基本出发点。为了量化众多的转捩影响因素，转捩建模中需要引入经验关系式。原始γ-Reθt 转捩模型主要考虑的是来流湍流度Tu和压力梯度λθ 的影响，因此转捩动量厚度雷诺数的经验关系式可写为Reθt =f（Tu，λθ ），对于粗糙壁面需要引入粗糙度作为新的影响因素。
1.2.1 转捩模型粗糙壁面经验关系式修正
本文引入了Stripf等［17］建立的粗糙壁面转捩动量厚度雷诺数，对于有量纲等效粗糙元高度ks 超过1%边界层位移厚度δ *的情况采用通过实验数据拟合的新关系式，即
式中：Reθt =f（Tu，λθ ）为原始γ-Reθt 转捩模型的边界层转捩动量厚度雷诺数经验关系式。
有效湍流强度函数为
有效湍流度为
式中：θ为边界层动量厚度；δ为边界层实际厚度；n为常数，对于Blasius层流边界层取为7。计算时首先采用Reθt 的定义式和经验关系式迭代求解当地化边界层转捩动量厚度θt，再通过式（16 ）、（17 ）得到相应的边界层位移厚度δ *。
1.2.2 程序实现
考虑粗糙度影响的转捩动量厚度雷诺数经验关系式为分段函数，接近光滑表面时仍使用原始经验关系式Reθt，这也为设置局部粗糙度提供了便利。在原始γ-Reθt 转捩模型程序基础上，将转捩判据改为分段函数Reθt ，rough，设置粗糙壁面起始与结束位置，通过网格节点坐标选择需要调用的转捩动量厚度雷诺数经验关系式及是否启动湍流模型粗糙壁面边界条件，以实现全局/局部粗糙壁面边界层流动模拟。最后，为了模拟粗糙壁面诱导转捩，需要同时考虑表面粗糙度对边界层转捩和湍流边界层发展的影响，这就涉及到粗糙壁面湍流模型边界条件和引入粗糙度影响后的转捩模型耦合使用的合理性。理论上看，两者对边界层流动模拟的作用分别体现在转捩后湍流的发展和转捩起始位置两个不同方面，即随着引入粗糙度影响的转捩模型发挥作用（触发转捩），湍流模型及其粗糙壁面边界条件的影响逐渐被引入转捩和湍流边界层；由于转捩过程中湍流模型未完全启动，因此粗糙壁面边界条件的作用也比较有限，主要影响充分发展的湍流边界层的流动特性。因此从模型原理出发，两种修正的作用阶段相对独立，耦合使用具有合理性，但仍需通过算例进一步验证说明。
2 算例应用与结果分析
本文计算均基于结构网格，采用风雷软件LU-SGS时间推进方法求解RANS方程和k-ω SST湍流模型、γ-Reθt 转捩模型方程，空间离散采用有限体积法二阶Roe格式。有关控制方程、数值算法的具体形式及计算参数设置可参见风雷软件手册［25］。本文所有算例均给定温度为室温15℃（即288K）的来流条件。考察斯坦顿数的算例设为等温壁面（算例中将给出壁面温度），其他算例设为绝热壁面。
2.1 零压力梯度平板
本算例所用网格和边界条件与1.1.4小节相同，来流条件根据不同工况进行设置。
2.1.1 MSU粗糙平板湍流边界层
Hosni等［26-27］研究了半球形粗糙沙粒对平板湍流边界层流动的影响，来流速度为12 m/s和58 m/s（对应来流单位雷诺数分别为0.8×106和3.9×106），壁面温度为300 K，等效粗糙度ks 为1.095 mm和0.293 mm，分别记为MSU（Mississippi State University）1~4平板。图4给出了采用两种不同湍流模型修正的计算结果与实验值的对比。从图4可以看出，粗糙度导致表面摩擦系数增大。与光滑平板相比，随着来流雷诺数（来流速度）的增大，边界层厚度减小，同一粗糙度水平（图4a和4b、图4c和4d）带来的摩擦系数增量有所降低；而对于同一来流状态（图4a和4c、图4b和4d），高粗糙度水平对应的壁面摩擦系数明显高于低粗糙度水平，ks =1.095 mm时摩擦系数约为光滑平板的2倍。Hellsten模型得到的摩擦系数在各个条件下均大于Knopp模型，且整体来看与实验结果更为吻合，但在低速状态下（图4a和4c）湍流边界层发展初始阶段的摩擦系数模拟结果与实验数据有一定差距。
2.1.2 双尺度平板边界层转捩
Wang等［28］、Abbott等［29］开展了双粗糙度壁面边界层转捩实验，研究了上下游不同粗糙度水平对于边界层转捩的影响，如图5所示。其中平板前缘砂纸带长5 cm，下游砂纸带覆盖平板剩余表面，长度延伸至2 00 cm。表2给出了实验中使用的3种不同规格的砂纸参数。目数实际是筛网的开孔单位，指单位面积筛网上能够完整开孔的数量，即能开10个完整的孔为10目，能开100个完整的孔为100目。目数越大，孔的直径越小。对于砂纸上粗糙颗粒也可做类似定义。在取样长度内，Ra 为表面纵坐标绝对值的算术平均值，Rz 为表面纵坐标峰谷值的平均值［30］。可见Rz 更接近于实际粗糙度水平的含义，故选择Rz 作为粗糙度输入参数。由于本文引入的粗糙壁面转捩动量厚度雷诺数经验关系式并未考虑双尺度粗糙度情形，因此暂不具备精确的变粗糙度模拟能力，接下来的算例仅针对实验中的光滑平板和局部粗糙平板进行计算。
表3 平板边界层转捩计算条件 |
| U inf /（m·s-1） | Re unit/106 | Tu inf /% |
|---|---|---|
| 4.6 | 0.31 | 0.2 |
| 4.6 | 0.31 | 3.3 |
| 4.6 | 0.31 | 5.0 |
| 8.6 | 3.34 | 0.5 |
来流单位雷诺数为3.34×106、湍流度为0.5%状态下不同粗糙度平板（含光滑）的边界层转捩计算结果与实验值的对比如图6b所示，Hellsten模型和Knopp模型标识的结果均为与粗糙壁面转捩模型耦合模拟的结果，其中40和60目砂纸为前缘局部粗糙，100目砂纸为全表面粗糙。相比于光滑平板，粗糙壁面使得转捩位置明显前移，并随着前缘粗糙度增大（砂纸目数减小）前移量不断变大。两种耦合模拟在各粗糙度水平下均预测到了边界层转捩，但从转捩位置上看，耦合Hellsten模型的转捩模型模拟结果与实验吻合较好，但仍然存在层流和转捩区斯坦顿数计算值偏低的问题。相比之下，耦合Knopp模型得到的转捩位置雷诺数均延后了约2×105，效果不佳。此外，由于Knopp模型对湍动能k的边界条件也进行了修正，导致与转捩模型耦合时计算稳定性变差。上述各状态均是在层流计算收敛结果的基础上进行续算得到的，Knopp模型耦合粗糙壁面转捩判据无法直接完成稳定计算。
该实验研究还表明在前缘粗糙带下游添加较小的第二粗糙带，在某些组合下会使边界层转捩延后，这可能与双尺度粗糙元高度变化对不稳定涡的抑制作用有关［30］。
2.2 NACA 652A215翼型
由于原始实验中光滑翼型的升力测量值偏低，因此改用Re=3.0×106下NACA652A215翼型的实验结果［29］，两种翼型低速条件下最大升力系数相差3%左右。两种粗糙壁面湍流模型修正的升力曲线计算结果与实验值的对比如图8所示。相比于光滑翼型，不同粗糙度水平均使翼型失速攻角减小4°左右，而较高的粗糙度水平会导致较大的升力损失（约36%）。对于过渡粗糙壁面（图8a），采用Hellsten模型的模拟结果更接近实验数据，Knopp模型虽然得到了与实验一致的失速攻角，但升力系数本身基本与光滑翼型计算结果一致，并未反映出粗糙度应有的影响；对于完全粗糙壁面（图8b），两种湍流模型修正的模拟结果接近且与实验吻合较好。图9进一步给出了8°攻角下不同粗糙翼型表面压力分布形态（粗糙壁面由Hellsten模型计算），可见过渡粗糙壁面翼型的压力分布形态与光滑翼型差别不大，但达到完全粗糙后，上下表面压力分布形态聚拢，导致升力系数显著减小。
图10为8°攻角下翼型附近涡黏性系数分布对比（粗糙壁面由Hellsten模型计算）。可以看出，上表面前缘和下表面后缘附近近壁区涡黏性系数（即雷诺应力）随表面粗糙度变大而显著增大，直接导致摩擦阻力增大。同时，较大的雷诺应力向下游输运将使得边界层明显变厚，使流动在相同压力梯度下更容易发生分离。
2.3 NACA 0012翼型
2.3.1 前缘粗糙湍流边界层
2.3.2 局部粗糙边界层转捩
NACA0012翼型局部粗糙边界层转捩实验由Kerho等［33］在伊利诺伊大学的亚音速风洞中完成，来流马赫数为0.1，弦长为0.534 m，基于弦长的雷诺数分别为0.75×106和2.25×106。翼型前缘不同位置处黏贴了粗糙带，粗糙颗粒高度为350 μm（ks /c≈6.55×10-4），粗糙带长度l、粗糙带起始位置s以及对应的粗糙带前后缘位置（沿弦长位置和沿表面位置）如表4所示。由于2.1.2节已经验证了Knopp模型与粗糙壁面转捩模型耦合效果不佳，且计算稳定性差，本节仅使用Hellsten模型耦合粗糙壁面转捩模型进行计算。计算中设置来流湍流度为0.1%，湍流涡黏性比为5，开启自由流湍流度衰减抑制［21］。
表4 粗糙带前后缘位置［33］ |
| 算例 | 粗糙带长度l/mm | 粗糙带起始位置s/mm | 沿弦长/c×10-3 | 沿表面/c×10-3 | ||
|---|---|---|---|---|---|---|
| 前缘 | 后缘 | 前缘 | 后缘 | |||
| 1 | 3.175 | 7 | 4.90 | 9.10 | 1.31 | 19.10 |
| 2 | 6.350 | 7 | 4.90 | 13.80 | 1.31 | 25.00 |
| 3 | 12.700 | 4 | 1.87 | 19.10 | 7.50 | 31.30 |
| 4 | 12.700 | 24 | 31.40 | 53.90 | 45.00 | 68.80 |
通过图13给出的翼型上表面摩擦系数来判断转捩起始与结束位置，并通过箭头标注在实验结果堆积图中进行对比（图14）。从图14可以看出，对于低雷诺数状态（图14a），实验结果显示，表3中前3个粗糙带布置的边界层转捩位置和转捩区长度粗糙带长度和粗糙带位置变化较小。Hellsten模型耦合粗糙壁面转捩模型得到的转捩位置及其变化趋势与实验结果基本一致，但由于本文修正并未考虑粗糙度对转捩过程的影响，模拟得到的转捩区长度没有明显变化。对于算例4状态，计算转捩位置虽也较算例3略向上游移动，但与实验结果相差较大。与算例3相比，实验结果显示，粗糙带位置后移约0.03 c（s=24 mm）反而使转捩大幅度前移，这不但与边界层转捩源于上游不稳定性历史累计效应的认知相悖，也不符合实验本身［33］给出的“转捩区域对粗糙带位置不敏感”的结论。实验结果有待进一步确认。
相比于低雷诺数状态，对于较高雷诺数状态（图14b），原始转捩模型捕捉到了光滑翼型转捩位置前移及转捩区长度变小。对于粗糙翼型，实验结果显示转捩发生在翼型前缘0.05c之前，且转捩区域长度均超过了40%c，转捩结束位置随粗糙带变长逐渐前移。计算结果反映出了转捩区域整体前移的趋势，但转捩位置和转捩区长度与实验结果差别仍然较大。
3 结论
本文基于国家数值风洞风雷软件，通过引入粗糙壁面湍流模型边界条件和转捩动量厚度雷诺数，实现了局部/全局粗糙壁面边界层流动模拟，主要结论如下：
（1）粗糙壁面会使边界层转捩提前发生，同时导致外形的摩擦阻力显著增大，近壁区雷诺应力的提前生成也使得湍流边界层变厚，加剧了较大攻角下的后缘分离。对于全湍状态翼型，粗糙度均造成了失速攻角4°左右的损失，ks /c=1×10-3量级的粗糙度将使最大升力系数下降约36%。
（2）整体来看，Hellsten等提出的针对k-ω SST湍流模型粗糙壁面修正能够较准确地反映粗糙度的影响（特别是对于过渡粗糙状态），全湍状态下气动力计算结果与实验值基本吻合，流场模拟结果符合粗糙壁面流动特征，同时仅改变比耗散率边界条件的方式也能够保证与转捩模型的稳定耦合计算，适合粗糙壁面边界层流动模拟工程应用。
（3）针对粗糙壁面的湍流模型和转捩模型修正的作用阶段和对模拟结果的影响相对独立，但需考虑耦合使用的计算稳定性问题。本文引入的Stripf等粗糙壁面转捩厚度雷诺数对于转捩位置及其变化趋势的模拟结果相对可信，但修正未涉及转捩区长度，同时基于风雷软件的实现可能存在层流区计算精度及斯坦顿数处理误差问题，还需后续研究解决。