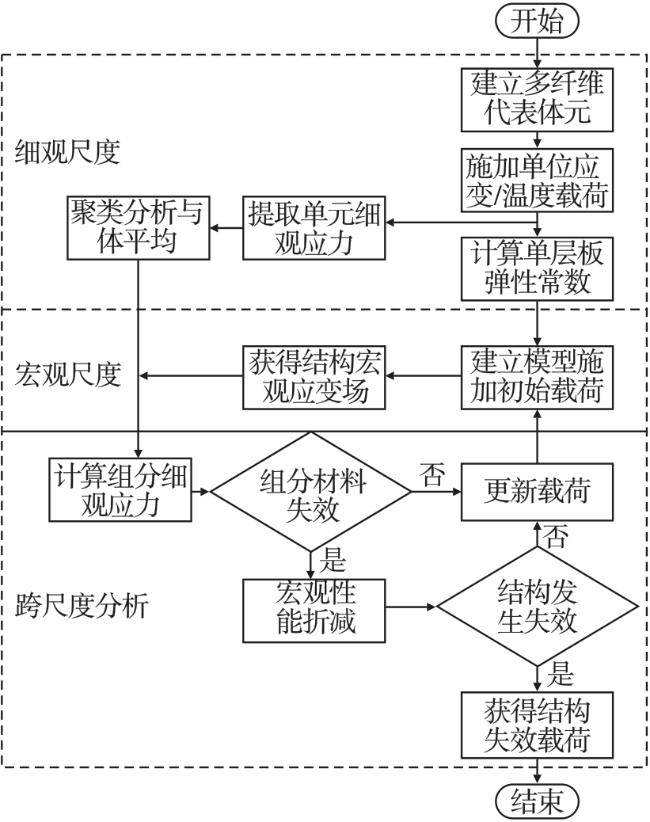
推进剂贮箱是航天运载器动力系统与结构系统的关键部件，承担着传递载荷与盛装燃料的作用，其质量约占结构总质量的60%左右［1］。相比于铝合金贮箱，低温铝合金内衬/无内衬复合材料贮箱能够实现减重20%~40%的目标［2］，其中，无内衬贮箱轻量化效果更好，但设计难度也更大［3］。复合材料贮箱设计中不仅要关注结构的稳定性，更需关注贮箱是否发生功能失效。由于贮箱在服役过程中同时承受机械载荷和低温载荷，复合材料中纤维与基体的热不匹配性会引起不可忽略的细观应力［4］，可能直接导致复合材料树脂基体失效、产生微裂纹，进而引起燃料泄漏导致复合材料贮箱发生功能失效。如X-33飞行器所采用的多瓣蜂窝夹层结构液氢贮箱，测试时复合材料层压板中的热应力促进了微裂纹的产生，最终引起了燃料渗漏，导致试验失败［2，5］。因此，分析无内衬复合材料贮箱中组分间热应力对贮箱失效的影响十分关键，使用基于经典层合理论及宏观失效准则的传统宏观分析方法无法考虑纤维与基体之间的热应力，需对无内衬复合材料贮箱开展考虑宏细观特征的跨尺度计算研究。
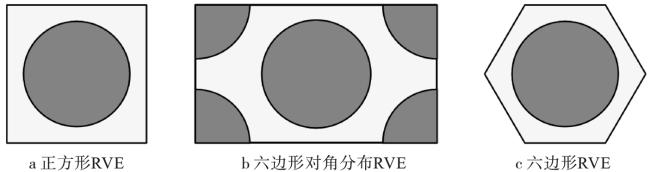
近年来，跨尺度分析在工程领域得到了快速的发展。Mayes等［6］提出了多连续体理论（multicontinuum theory），基于三角形代表体元（representative volume element，RVE）得到了材料的本构，并对纤维基体分别进行了失效判断。李星等［7］提出了基于应力的复合材料跨尺度失效准则，通过对正方形RVE与六边形RVE选取参考点求得宏观至细观的应力放大系数，建立了损伤判定与损伤演化的方法，跨尺度计算与试验结果吻合较好。Huang等［8］针对低温复合材料贮箱力学性能评价问题提出了跨尺度分析方法。在细观尺度上，用基于六边形RVE来表征复合材料细观组分，对贮箱开展渐进失效分析并与Tsai-Wu准则进行了对比。任明法等［9］采用了基于六边形RVE的宏细观一体化分析方法，开展了复合材料跨尺度分析。结果表明，在温度载荷下，对基体采用细观最大应力准则可以有效地预测复合材料贮箱基体开裂。常鑫［10］提出了考虑制造缺陷的复合材料多尺度分析方法，并建立了相应的多尺度分析框架，对复合材料机翼盒段结构与复合材料贮箱结构开展研究，获得了两种结构的失效模式与失效载荷。Tian等［11］建立了六边形RVE并采用局部精确均匀化理论（locally exact homogenization theory）获得了不同破坏模式碳纤维复合材料的刚度退化系数，并基于Hashin准则与最大应力准则对低温贮箱进行了跨尺度渐进损伤分析。上述方法能够获得比较准确的预测结果，但因为他们所采用的RVE中仅包含单根纤维，所以未考虑温度作用下多纤维引起的基体局部应力集中现象。González等［12］证明了包含30根纤维足以表征单向复合材料细观特征。杨雷等［4］研究了温度的纤维分布形式对单向复合材料强度的影响，结果表明纤维随机分布的最大热应力比周期性分布的情况明显偏大，热应力的存在降低了复合材料的横向拉伸/压缩强度。多纤维RVE的效果虽然好于单纤维RVE，但对于贮箱结构而言，跨尺度渐进损伤分析需在多个尺度间开展参数传递，包含多根纤维的RVE分析效率较低，限制了其应用。
为了提高跨尺度计算效率，对多纤维RVE中单元采用聚类方法可减少RVE自由度。Liu等［13］提出了自洽聚类分析（self-consistent clustering analysis，SCA），在离线阶段，使用k-means聚类对具有相似力学行为的材料进行聚类以实现数据压缩；在在线阶段，宏观有限元模型与压缩后的材料信息进行实时传递计算，形成了FEM-SCA的跨尺度计算方法。随后Liu等［14］将SCA方法应用于应变软化问题，通过用户定义材料实现每一个积分点处包含微损伤算法的SCA模型，开展了双开孔板的拉伸跨尺度分析，获得了宏观模型中不同积分点的微观应力场和损伤场。Han等［15］基于FEM-SCA方法，提出了编织复合材料的多尺度分析方法，获得了T型结构在循环弯曲作用下宏观尺度与中尺度的应力、应变场及材料的非线性行为。张力等［16］将微观界面纳入多尺度失效分析中，采用缩聚后的放大因子进行多尺度信息传递，并对2D编织SiC/SiC复合材料开展了渐进损伤失效分析。王猛［17］基于改进的微观力学失效理论多尺度方法预测了编织复合材料拉伸性能，并开展了含孔编织材料拉伸失效分析与编织复合材料板的冲击失效分析研究，验证了其多尺度方法的有效性。上述研究均表明，使用k-means聚类方法对RVE中单元进行缩聚，能够有效地提高跨尺度计算效率。
为此，本文建立了多纤维的RVE，采用k-means聚类方法对RVE单元进行聚类分析，降低了多纤维RVE在跨尺度分析中的计算成本。通过对IM7/977-3复合材料力学性能参数及复合材料单向板强度的预测，证明了该方法的准确性，并建立了基于多纤维RVE和聚类分析的复合材料贮箱跨尺度分析框架。
1 细观力学模型
1.1 多纤维代表体元
在跨尺度分析中，细观尺度下通常以代表单元为研究对象，因此，合理地选取代表单元十分重要［18］。在建立单向复合材料RVE时，RVE中纤维的分布形式主要有两种：一种是认为纤维在空间上是规则排列的，建立的代表体元有正方形RVE、六边形对角分布RVE与六边形RVE等，如图1所示。学者们基于此类RVE开展了相关研究［6-8］，并取得了一定的成果；另一种是采用多纤维RVE，即单个RVE中包含多根纤维。显微照片下实际的纤维分布如图2a所示，对于高体分比的复合材料而言，一般认为其纤维分布存在一定的统计规律，纤维之间的距离与角度由制造过程确定，生成与实际纤维间距离、夹角分布具有相似统计规律的RVE，这种形式的RVE受载荷时能够将相邻纤维间存在的应力集中现象体现得更好。学者们开发出了如随机序列膨胀法（random sequential expansion，RSE）等生成算法［19］，用于生成包含多根纤维的RVE。本文针对单向复合材料，建立多纤维的正方形RVE用于表征复合材料细观尺度上的特征。RVE中纤维的体分比为70%［20］，包含40根直径为 的纤维，边长 ，厚度 。RVE及网格模型如图2b所示。
1.2 周期性边界条件
1.3 等效参数计算方法
单向复合材料可视为正交各向异性材料，其热力学本构如式（2） 所示。
式中： 、 分别为第k个单元中第i个应力分量与单元体积；N为RVE中总单元数；V为所有单元总体积。若不考虑应变载荷，对RVE施加单位温度载荷，由等效刚度矩阵 C 与式（4） 可求解获得热膨胀系数。
1.4 强度准则与刚度折减模型
2 复合材料跨尺度分析方法与聚类分析
2.1 跨尺度分析方法
为了得到贮箱结构在宏观响应下细观组分场的应力，本文采用Huang等［8］提出的分层级跨尺度分析方法获得复合材料中纤维与基体的应力场。任一点的细观应力由该点在宏观尺度上的响应计算而来，叠加公式如式（6） 所示。
式中： 为宏观结构中积分点处的应变； 为温度变化量； 与 分别为6组单位应变载荷与1组单位温度载荷下RVE中积分点的应力场； 为当前积分点处温度与宏观应变作用下的细观应力场。
2.2 k-means聚类分析
表2 应力信息格式 |
| A 积分点 | … | … | ||||
|---|---|---|---|---|---|---|
| Ele1，int1 | 281070 | … | 3476.0 | 0.1549 | … | |
| Ele1，int2 | 281070 | … | 3476.0 | 0.1549 | … | |
| Ele2，int1 | 281080 | … | 3199.5 | 0.1548 | … | |
| ︙ | ︙ | ︙ | ︙ | |||
| EleN，int1 | 281090 | … | 3782.5 | 0.1547 | … | |
本文将RVE中包含的纤维基体单元进行聚类，其中每一类中的单元在空间上可以是不连续的。对每一类中的应力信息进行体平均，将获得的等效应力信息代替原RVE中的应力信息用于跨尺度细观应力计算。使用跨尺度分析方法，本文认为由宏观响应与等效应力信息计算的组分细观应力满足失效条件时，即认为该类中所有单元发生失效，从而导致RVE发生失效。根据1.4节强度准则与刚度折减模型，对发生失效的单元采用细观失效判断、宏观性能折减的方式实现结构的跨尺度失效分析。结合2.1节，最终形成基于聚类分析的复合材料贮箱跨尺度分析方法，如图3所示。
3 复合材料贮箱跨尺度计算
3.1 等效参数预测
根据IM7纤维与977-3基体的力学性能，结合式（2 ）、（3 ）开展IM7/977-3复合材料单层板的等效参数预测，所得结果如表5所示，最大误差为0.9%，单层板等效参数预测值与试验结果取得很好的一致性，验证了所建立RVE模型的合理性。
表5 单层板等效参数预测值与试验结果［20］对比 |
| 材料参数 | 试验 | 预测结果 | 误差/% |
|---|---|---|---|
| 193.39 | 194.6 | 0.6 | |
| 8.85 | 8.81 | 0.4 | |
| 4.67 | 4.658 | 0.2 | |
| 0.32 | 0.317 | 0.9 |
3.2 单向板跨尺度强度预测
从纤维与基体的力学参数出发，基于2.2节中所建立的包含多纤维和聚类分析的复合材料贮箱跨尺度分析方法，开展单向板跨尺度强度预测。建立的单向板有限元模型中长、宽、总厚度及单层厚度分别为160、40、2、0.125 mm，铺层为 。首先，对建立的RVE施加７组单位载荷，根据2.2节与式（3） 对RVE中纤维与基体分别开展聚类与体平均，所得的等效应力信息被用于细观失效的计算。随后，结合式（6） 所示的跨尺度分析方法实现计算组分应力，并依据强度准则判断组分失效，对发生失效的单元进行相应的刚度折减，最终实现单向板跨尺度强度预测。分别对模型开展纵向拉伸、纵向压缩、横向拉伸与横向压缩等载荷下单向板强度性能计算。单向板有限元模型如图4所示，模型共包含约150 000个实体单元。
表6 直接求解与聚类降阶求解对比 |
| 不同求解方案 | 单元数/聚类数 | 未知 量数 | 计算 时间/s |
|---|---|---|---|
| 直接求解 | 115 866 | 811 062 | 76 920 |
| 聚类-16-16 | 32 | 224 | 704 |
| 聚类-24-24 | 48 | 336 | 714 |
| 聚类-32-32 | 64 | 448 | 719 |
3.3 复合材料贮箱跨尺度分析
贮箱作为存放燃料的部件，服役于极低的温度环境下并承受一定的内压载荷，首先要确保结构的盛装性能［24］。组分材料中纤维强度远高于基体强度，导致基体比纤维早一步发生失效，由此形成微裂纹，可能引起燃料泄露。因此，应重点关注组分材料中基体失效情况。基于3.2节中的结果，本节采用前文建立的基于聚类的跨尺度方法与折减模型对低温复合材料贮箱开展强度预测。选取纤维基体聚类数均为16，采用基体穿孔［24］作为贮箱最终失效模式，即认为某位置所有单元均发生基体失效则该结构发生失效。假设纤维性能不随温度发生变化，基体性能与温度有关，如表4所示。根据1.3节内容对-253 ℃低温下复合材料参数进行预测，复合材料在低温下的性能与常温性能有所不同，如表8所示。贮箱几何参数如表9所示，铺层为 。建立的1/8贮箱有限元模型如图6所示，共包含大约220 000个实体单元。贮箱有限元模型边界上施加对称边界条件，定义初始温度为20 ℃，降至工作温度-253 ℃后，逐渐施加内压增量0.015 MPa，开展该贮箱跨尺度渐进失效分析。
复合材料贮箱的跨尺度渐进失效过程如图7所示，此处仅展示贮箱第1、3、15层分别在载荷0.86、0.90、0.95 MPa时的损伤情况。标记为深灰色的单元表示单层中发生的基体失效区域，标记为黑色的单元表示该区域基体未发生失效。结果显示，载荷为0.86 MPa时基体失效首先出现于第3层中直筒段与封头段交汇处，随着载荷增加失效区域向贮箱直筒段和厚度方向扩展，最后在载荷0.95 MPa时，复合材料贮箱中发生了基体贯穿失效，形成了渗漏通道导致此时贮箱发生功能失效。
4 结论
本文基于多纤维RVE，采用k-means聚类方法对RVE中的单元进行聚类开展降维计算，建立了基于聚类分析的复合材料贮箱跨尺度分析方法，给出了完整的实施流程，并与文献中的试验结果进行了对比验证，得到主要结论如下：
（1）本文所提方法能够基于纤维和基体的性能准确地预测复合材料单向板的弹性常数及破坏强度，误差在10%以内。
（2）本文研究基于一个受温度与内压载荷共同作用的贮箱，结果表明，在-253 ℃、0.86 MPa内压作用下，该贮箱中基体失效首先发生在封头与直筒段连接处。随着内压增加失效区域也逐渐扩展，最终在0.95 MPa时发生基体穿孔，形成渗漏通道，此时贮箱发生功能失效。
（3）相比于传统的多尺度分析，本文所提方法未知量个数与计算时间分别降为原来的 与 ，具有较好的计算效率，能够快速实现复合材料贮箱的跨尺度失效预测。
（4）由于结构级试验的难度，目前仅从单向板层面开展了强度验证，但未对复合材料贮箱开展试验验证，可在未来开展此工作，针对结构级试验的失效位置和失效载荷开展进一步的验证工作。