Indoor location algorithm based on maximum entropy fuzzy probability data association

Xuan LI; Shijia XU; Ershen WANG

doi:10.3969/j.issn.2095-1248.2024.02.007

Journal of Shenyang Aerospace University >

2024 , Vol. 41 >Issue 2: 57 - 67

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.02.007

Information Science and Engineering

Indoor location algorithm based on maximum entropy fuzzy probability data association

Xuan LI ,
Shijia XU ,
Ershen WANG

Expand

College of Electronic Information Engineering，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2023-12-20

Online published: 2024-05-29

Fold

Abstract

Wireless sensor network is composed of multiple micro-sensor nodes， and location technology is one of the important applications of WSN. At present， many location algorithms have high location accuracy in line of sight （LOS） environment， but poor location accuracy in non line of sight （NLOS） environment. An improved maximum entropy fuzzy probability data association algorithm based on arrival time was proposed. The grouping idea was utilized to divide N measure- ment values into L groups， and each group obtained the corresponding mobile node position estimation， model probability and covariance matrix through the interactive multi model （IMM） algorithm. Afterwards， the obtained L position estimation was subjected to non line of sight detection through a validation gate. The position estimation contaminated by non line of sight errors was discarded， and the corresponding correlation probabilities was used to weight the correct position estimates to obtain the final position estimation. Simulation and experimental results show that the proposed algorithm can reduce the influence of non line of sight errors and achieve higher location accuracy than the existing methods.

Key words： wireless sensor network; indoor location; non line of sight; maximum entropy fuzzy probability; data association; time of arrival

Cite this article

Xuan LI , Shijia XU , Ershen WANG . Indoor location algorithm based on maximum entropy fuzzy probability data association[J]. Journal of Shenyang Aerospace University, 2024 , 41(2) : 57 -67 . DOI: 10.3969/j.issn.2095-1248.2024.02.007

移动节点定位是指使用某种方法来获得移动节点（mobile node，MN）的坐标信息。常用的定位方法主要分为测距和无测距两种。基于距离的方法主要包括到达时间（time of arrival，TOA）^［1］、到达时间差（time difference of arrival，TDOA）^［2］、接收信号强度指示（receive signal strength indication，RSSI）^［3］、到达角（angle of arrival，AOA）^［4］等。MN和信标节点（beacon node，BN）之间直接传输的信号称为视距传输。然而在现实中，信号通常不是直接在MN和BN之间传输，而是被障碍物阻挡进行了反射或折射，这种称为非视距传输，尤其在室内环境中，非视距情况更为严重。由于非视距环境中的传输距离比视距环境下的传播距离长，因此距离测量会产生较大的正偏差，即非视距误差，而非视距误差是造成定位不准确的主要原因。如何识别和减轻非视距误差是定位算法研究的热点和难点。

传统的非视距误差抑制算法主要集中在距离测量的滤波上。然而，这些算法在处理非视距误差较大的环境时，并不能达到较高的精度和较强的鲁棒性。因此，相关领域作者提出了许多混合技术来处理这些问题^［5］。鲁棒多模型交互（robust interacting multiple model，RIMM）算法^［6］使用扩展卡尔曼滤波器（extended Kalman filter，EKF）和鲁棒扩展卡尔曼滤波器（robust extended Kalman filter，REKF）进行滤波。REKF的鲁棒性和更好的滤波效果使RIMM算法有效地减小NLOS误差的影响。但REKF的滤波参数

c 1 、 c 2

需要手动设置，这在处理复杂的NLOS环境时是困难且不灵活的。概率数据关联（probability data association，PDA）^［7］基于贝叶斯滤波的框架，将目标的状态估计表示为概率分布，通过观测来更新和修正目标状态的概率。PDA算法在多目标跟踪中具有较好的性能，特别是在存在目标遮挡、观测噪声和数据关联不确定性的复杂场景中。它可以提供目标状态的概率估计，对不确定性进行建模，并能够处理观测缺失和错误关联的情况。需要注意的是，PDA算法的计算复杂度较高，尤其在目标数量较多和观测空间较大的情况下。修改的概率数据关联（modified probability data association，MPDA）是对概率数据关联的改进^［8］，然而在某些方面，它的表现并不那么好。例如，当识别NLOS和LOS误差时，若非视距的情况非常复杂，MPDA会遵循先前的卡尔曼预测状态和协方差，这将导致视距误差被误判为非视距，使识别不准确，这就需要一种更有效的识别方法。文献［9］提出了基于贝叶斯准则的联合概率数据关联（joint probability data association，JPDA）来跟踪多个移动目标。JPDA通过列举所有可行的联合事件来计算多个目标的联合后验关联概率，但在实践中，无法知道检测概率和杂波率，其决定了JPDA的最终估计性能。He等^［10］提出将JPDA滤波器与泊松点过程（poisson point process，PPP）出生模型和多重伯努利滤波器相结合，这种改进的JPDA算法可以适应未知的检测概率和杂波率，并且在完全了解检测概率和杂波率的情况下，所提出的JPDA滤波器可以快速恢复理想JPDA滤波器的性能。修改的联合概率数据关联（modified joint probability data association，MJPDA）^［11］是对JPDA的改进，用于跟踪单个目标，对于非视距削弱效果比概率数据关联效果更好，这些问题是当下的研究热点。文献［12］提出了一种渐进相对效率的方法，并在此基础上设计了新的混合假设检验，用于提高WiFi室内定位的准确性。与传统的WiFi定位相比，作者不仅考虑了信号分布的多样性，还考虑了接收信号强度测量值的误差，从而提高了定位精度。

非视距识别方法可以有效地消除非视距误差对定位精度的影响。HAN等^［13］提出一种基于RSSI/PDR的概率位置选择算法，该算法基于接收信号强度指示、混合视线和非视距环境下的行人航位推算，用于低复杂度识别。文献［14］提出了一种基于多维尺度（multidimensional scale，MDS）和准精确检测（quasi-accurate detection，QUAD）的NLOS识别方法。该方法仅依赖于距离测量，并且独立于测量误差估计模型。此外，利用高维空间中的网络拓扑约束，可以通过多次迭代来校正识别的距离，从而可以很好地识别和校正非视距误差。文献［15］提出了一种位置受限的随机推理算法。一般来说，随机推理是以计算和信息交换的高成本为代价的，但该算法将节点的位置限制在一定的区域内，因此有助于推理算法集中于样本空间的重要区域，而不是整个样本空间。文献［16］应用机器学习方法分析不同场景下的测量值，试图识别非视距传播条件下的测量，用来减小距离测量值与欧几里得距离之间的偏差，同时也适用于减轻估计的误差。

本文针对现有研究存在的不足，提出了一种基于最大熵模糊概率数据关联滤波器的移动目标定位算法。采用多次滤波技术削弱非视距误差，并利用最大熵模型获得最优的隶属度，使得定位结果更加准确。通过仿真和实验结果，验证了本文算法的有效性和优越性。

1 信号模型搭建

假设MN周围有N个BN来跟踪和定位它，将MN的状态向量建模为

X^(m) =

[x (m),

y (m),

x ˙ (m), y ˙ (m)] T

，

(x (m), y (m))

表示MN在时间

m

的二维位置，

(x ˙ (m), y ˙ (m))

，表示MN的速度。MN在二维坐标系中移动，MN的状态向量的改变被建模为

X^(m) = F X^(m - 1) + w

（1）

F = 10 T s 0 010 T s 00100001

（2）

式中： F 为状态转移矩阵；

w

为测量噪声矩阵；

T s

为采样周期。本文采用了基于TOA的定位方法，通过UWB无载波通信技术获得了信标节点与移动节点之间的距离。在时间步长

m

下，BN和MN之间的TOA距离测量可以表示为

d ˜ = h n X^(m) + k

（3）

式中：

h n X^(m)

为BN和MN之间的欧式距离。在任意

m

时刻，可以得到一个欧式距离集

h X^m = h 1 m, h 2 (m), …, h N m T

，它包含了所有信标节点与移动节点之间的距离信息。在LOS情况下，

k

是测量噪声，即系统噪声；在NLOS情况下，

k

是测量噪声和非视距误差引起的噪声之和。

第

n

个BN和MN之间的距离定义为

h n X^(m) = (x (m) - x B S n) 2 + (y (m) - y B S n) 2 n = 1,2, …, N

（4）

式中：

(x B S n, y B S n)

代表第n个基站的坐标；N代表基站的数量。

2 定位跟踪算法

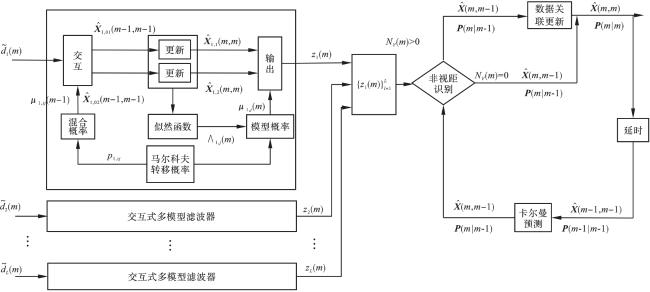
2.1 总体思想

最大熵模糊概率数据关联滤波器算法的流程如图1所示。采用分组的思想将N个测量值分为L个不同的组。每组获得相应的位置估计

Z l (m) = [x l (m), y l (m)] T

和一组模型概率

[μ l, 1 (m), μ l, 2 (m)]

，用于通过IMM-EKF进行非视距识别。如果组l中的BN和MN都处于LOS环境中，则组l的位置估计具有高精度；如果组l中的BN和MN中至少一个处于非视距环境中，则组l获得的位置估计将受到非视距的干扰。通过IMM-EKF可以减小一些非视距误差。为了进一步减轻NLOS误差对MN位置估计的影响，使用假设检验来识别位置估计是否受到NLOS误差的干扰，在验证门外的位置估计将被丢弃，未被非视距误差干扰的将被视为正确的位置估计。如果正确位置估计的数量大于0，则计算关联概率以更新状态估计，否则将使用预测的状态估计和协方差矩阵估计作为最终的结果。

显示原图|下载原图ZIP|生成PPT

图1 算法结构图

2.2 分组和IMM-EKF估计

假设在MN周围有N个BN来定位它，其中N至少大于3。N个BN被分为L（

L = C N 3

）个不同的组，并且通过IMM-EKF获得每个组的位置估计。当使用IMM-EKF时，对先验概率

μ l, i (m - 1)

、马尔可夫转移概率

P l, i j

、先验状态

X^l, i (m - 1 | m - 1)

和协方差矩阵

P l, i (m - 1 | m - 1)

分别进行初始化。

首先，进行输入交互计算，得到混合状态估计和混合协方差估计

μ l, i | j m - 1 | m - 1 = 1 / c ¯ l p l, i j μ l, i m - 1 l = 1, ⋯, L i, j = 1,2

（5）

c ¯ l = ∑ i p l, i j μ l, i m - 1

（6）

X^l, 0 j m - 1 | m - 1 = ∑ i X^l, i m - 1 | m - 1 · μ l, i | j m - 1 | m - 1

（7）

X^l, i j m - 1 | m - 1 = X^l, i m - 1 | m - 1 - X^l, 0 j m - 1 | m - 1

（8）

P l, 0 j m - 1 | m - 1 = ∑ i μ l, i | j m - 1 | m - 1 P l, i m - 1 | m - 1 + X^l, i j m - 1 | m - 1 X^l, i j T m - 1 | m - 1

（9）

根据交互结果进行模型匹配，预测状态估计和协方差估计

X^l, j m | m - 1 = F X^l, 0 j m - 1 | m - 1

（10）

P l, j m | m - 1 = F P l, 0 j m - 1 | m - 1 F T + C Q l m C T

（11）

C = T s 2 / 2 0 0 T s 2 / 2 T s 0 0 T s

（12）

式中：

C

为干扰噪声输入矩阵；

Q l m

为过程噪声协方差矩阵。

滤波更新

H l, j m = ∂ h X^l m ∂ X^l m | X^l m = X^l, j m | m - 1

（13）

其中

h n (X^l (m)) = (x (m) - x B S n) 2 + (y (m) - y B S n) 2

h (X^l (m)) = h 1 (m), h 2 (m), ⋯, h N (m) v l, j m =

d ∼ l m - h X^l, j m | m - 1

（14）

S l, j m = H l, j m P l, j m | m - 1 H l, j T m + R l, j m

（15）

式中：

v l, j m

是新息；

S l, j m

为更新协方差矩阵。

K l, j m = P l, j m | m - 1 H l, j T m S l, j - 1 m

（16）

X^l, j m | m = X^l, j m | m - 1 + K l, j m v l, j m

（17）

P l, j m | m = I 4 - K l, j m H l, j m P l, j m | m - 1

（18）

更新似然函数，计算模型概率

Λ l, j m = N v l, j m; 0, S l, j m

（19）

μ l, j m = 1 / c l Λ l, j m c ¯ l, j

（20）

c l = ∑ j Λ l, j m c ¯ l, j

（21）

交互输出

X^l m | m = ∑ j X^l, j m | m μ l, j m

（22）

P l m | m = ∑ j μ l, j m P l, j m | m + X l, j m | m ⋅ X l, j T m | m

（23）

X l, j m | m = X^l, j m | m - X^l m | m

（24）

根据交互式多模型滤波器的输出，计算每个子群的位置估计

z l m = B X^l m | m

（25）

B = 10000100

（26）

2.3 最大熵模糊概率数据关联算法

2.3.1 卡尔曼滤波

假设状态向量的初始值和移动节点的协方差矩阵分别为

X^(m - 1 | m - 1)

和

P (m - 1 | m - 1)

。

X^(m | m - 1) = F X^(m - 1 | m - 1)

（27）

P (m | m - 1) = F P (m - 1 | m - 1) F T + C Q C T

（28）

预测的位置估计被建模为

z (m | m - 1) = B X^(m | m - 1)

（29）

得到L个测量值和预测值之间的差值

v l (m) = z l (m) - z (m | m - 1), l = 1, ⋯, L

（30）

2.3.2 非视距识别

如果组和MN的3个BN都处于LOS环境中，那么

v l (m) ∼ N (0, S l (m)), l = 1, ⋯, L

（31）

S l (m) = B P (m | m - 1) B T + σ L 2 (H l T (m) H l (m)) - 1

（32）

式中：

S l (m)

是创新协方差矩阵。为了验证方程（31），定义了以下假设

ζ 0, l : v l (m) ∼ N (0, S l (m)), l = 1, ⋯, L ζ 1, l : n o t ζ 0, l, l = 1, ⋯, L

（33）

使用自适应验证门进行非视距识别。阈值

γ

的选择、验证区域的大小与阈值概率

P G

有关

P G = ∫ 0 γ f χ 2 (2) (x) d x = 1 - P F A

（34）

式中：

f χ 2 (2) (⋅)

是自由度为2的卡方分布；

P F A

是预设的虚警率。统计测试

T l (m)

建模为

T l (m) = v l T (m) S l - 1 (m) v l (m)

（35）

如果

T l (m)

不大于阈值

γ

，则假设

ζ 0, l

是真的。将落入验证门的位置估计作为正确的位置估计，并将它们的数量记录为

N V (m)

，否则假设

ζ 0, l

被拒绝。如果

N V (m)

大于0，则计算与正确位置估计相对应的关联概率，然后更新状态估计和协方差矩阵估计；如果

N V (m)

为0，则使用预测的状态和协方差矩阵作为更新的结果。

2.3.3 最大熵模糊概率数据关联

最大熵模糊概率数据关联滤波器（maximum entropy fuzzy probability data association filter，MEFPDAF）用于NLOS情况下的数据关联和更新，它的原理是使用最大熵模糊聚类方法对目标的候选测量值进行聚类，然后利用目标测量值的模糊隶属度重构关联概率。最大熵模糊聚类方法是基于模糊C-均值（fuzzy C-means，FCM）聚类的，FCM是一种基于目标函数的模糊聚类方法，假设有个数据集X，要划分为C个类，那么对应就有C个类中心，每个样本j属于某一类的隶属度为

u i j

。FCM的隶属度

u i j

与概率数据关联概率

β i j

之间具有相似的性质，因此

β i j

可以被复杂度较低的

u i j

所取代。将最大熵模糊概率数据关联滤波器应用于单目标跟踪时，即j=1，所有目标概率和相加为1。

∑ i = 1 N V (m) u i = 1, ∀ u i ∈ 0, 1

（36）

式中：

u i

是验证门中的测量值相比预测值的概率，成本函数为

E = ∑ i = 1 N V (m) u i d (z i (m), z (m | m - 1)

（37）

最大熵原理认为，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型（分布）。在本文中，使用最大熵原理建立熵最大的模型，来获得最优的隶属度。也就是说，将主要目标函数

J (U, C)

最大化，并使用拉格朗日方法，如式（38）所示。

J (U, C) = - ∑ i = 1 N V (m) u i l n u i + λ (∑ i = 1 N V (m) u i - 1) - α ∑ i = 1 N V (m) u i d (z i (m), z (m | m - 1))

（38）

式中：

α

和

λ

为拉格朗日乘子；

d (z i (m), z (m | m - 1))

是

z i (m)

和

z (m | m - 1)

之间的欧几里得距离。最终

u i

是

u i = e - α d (z i (m), z (m | m - 1)) ∑ i = 1 N V (m) e - α d (z i (m), z (m | m - 1)), i = 1,2, ⋯, N V (m)

（39）

最后，根据式（39）计算出的概率更新状态向量和方差向量。创新协方差矩阵

S (m)

和增益矩阵

K (m)

可由以下公式计算

S (m) = B P (m | m - 1) B T + σ L 2 I

（40）

K (m) = P (m | m - 1) B T S - 1 (m)

（41）

然后状态和协方差更新为

E (m) = ∑ i = 1 N V (m) u i (m) v i (m) u i

（42）

X^(m | m) = X^(m | m - 1) + K (m) E (m)

（43）

P (m | m) = (I 4 - K 2 (m) B) P (m | m - 1) + P ˜ m

（44）

P ˜ m = K (m) ∑ i = 1 N V (m) u i (m) v i T (m) v i (m) - E (m) E T (m) × K T (m)

（45）

3 仿真和实验

3.1 仿真

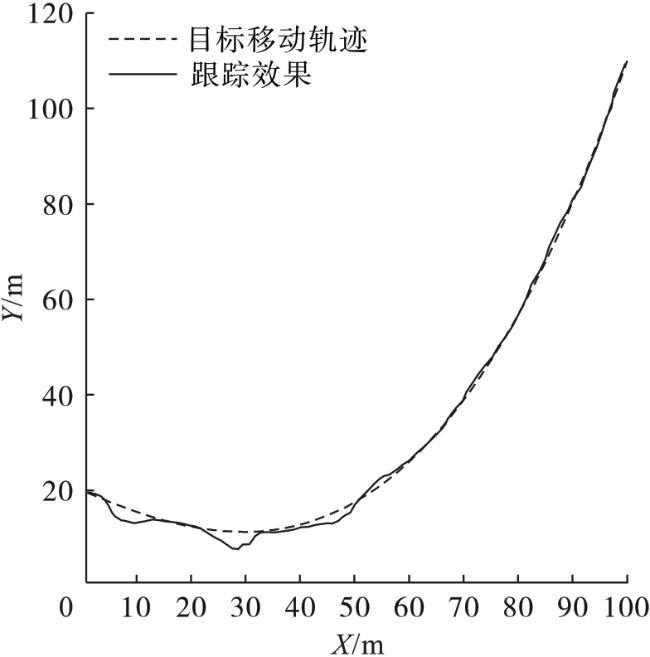
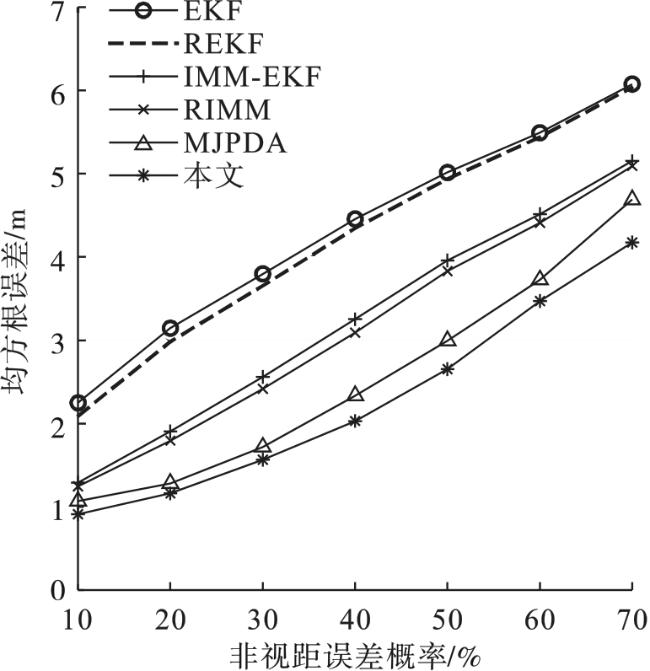
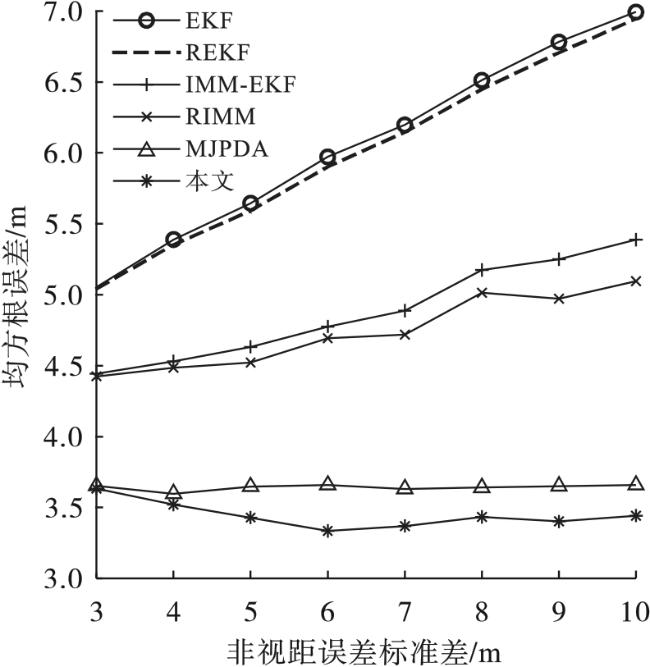
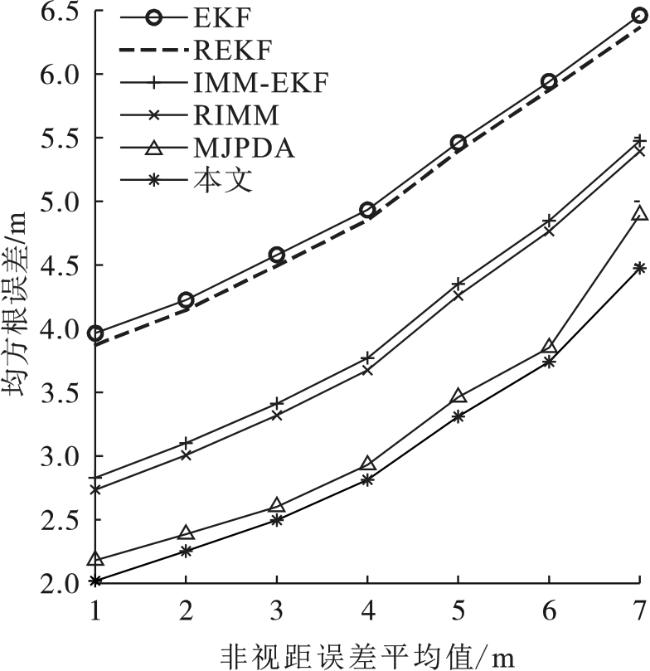
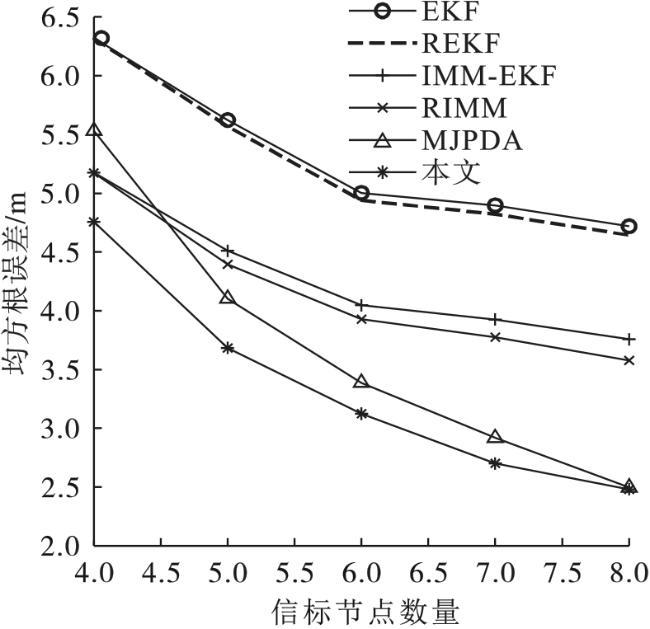
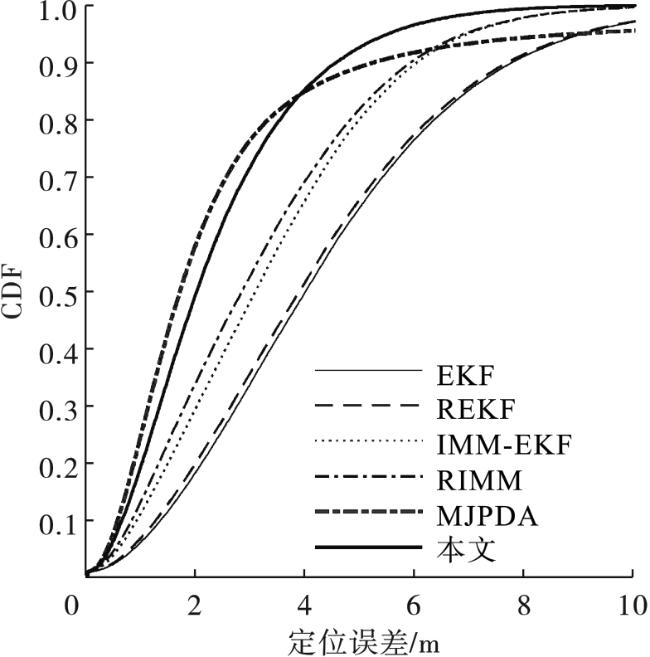
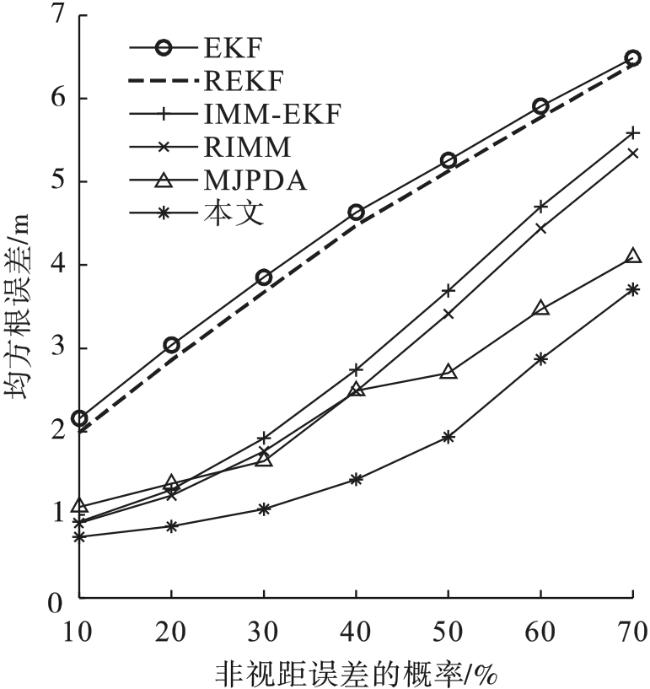
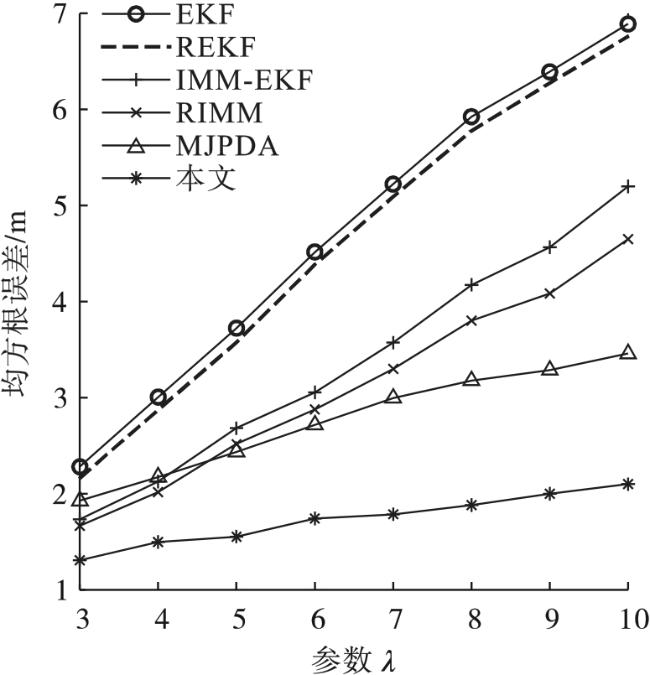
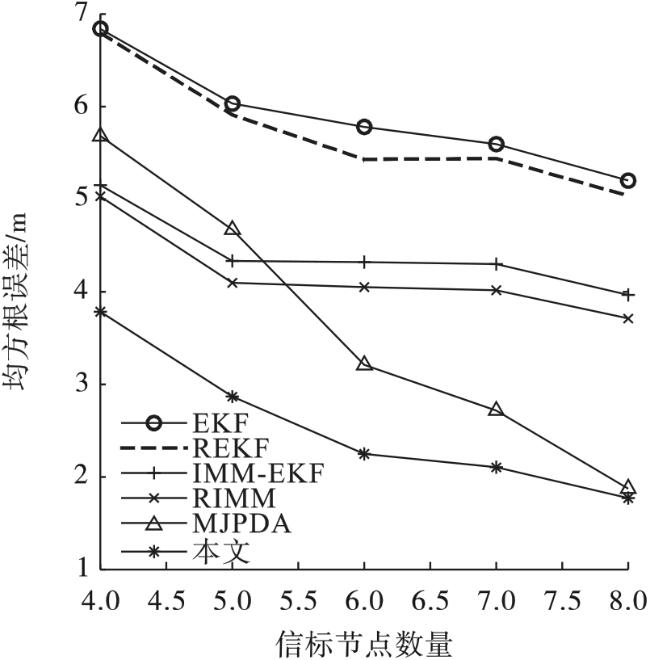
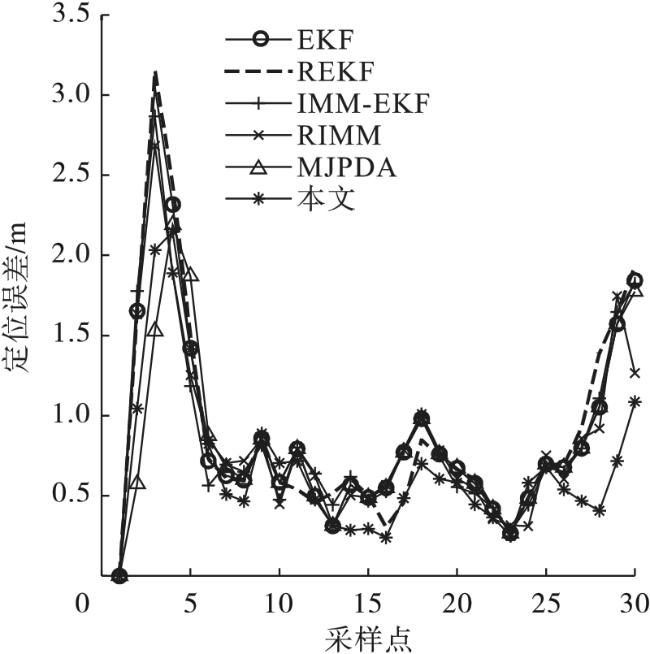
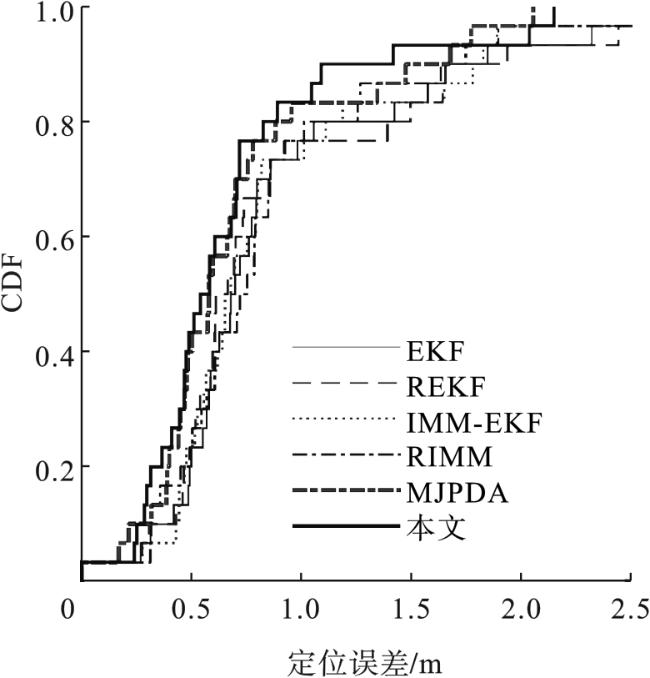
3.1.1 定位精度分析

本节重点介绍模拟和实验结果。在本文中，6个BN被随机部署在100 m×100 m的区域中。MN沿着图2所示的固定轨迹移动，移动步数为100。采样周期为0.5 s，移动节点的初始状态和协方差矩阵被设定为

X^(0) = [1 m, 20 m, 1 m / s, 0.5 m / s] T

和

P (0) = I 4

。初始状态设置为

X^l, j (0) = X^(0)

，协方差矩阵的初始值为

P l, j (0) = P (0)

。马尔可夫转移矩阵

P l, i j

的初始值为0.5。过程噪声协方差矩阵

Q l (0) = I 2

。测量噪声的协方差矩阵

R l, j (0) = I 3

。阈值概率

P G

为0.99，对应误报率

P F A

为0.01，检测概率

P d

设置为0.95。为了模拟非视距环境，随机生成一个概率值，将该概率值与NLOS概率进行比较，如果概率小于NLOS概率，则认为MN和相应的BN处于NLOS条件。仿真实验分别在非视距误差服从高斯分布和指数分布的条件下进行。将所提出的算法与EKF、REKF、IMM-EKF、RIMM和MJPDA进行比较。模拟结果是通过1 000次蒙特卡洛运行获得的。定位误差的均方根误差（RMSE）和误差累积分布函数（CDF）被用作评估算法的性能。

R M S E = 1 T 1 M C ∑ j = 1 M C ∑ m = 1 T (x^j (m) - x j (m)) 2 + (y^j (m) - y j (m)) 2

（46）

式中：

(x^j (m), y^j (m))

是在第j次蒙特卡洛运行期间获得的位置估计；

(x j (m), y j (m))

是MN在第j个蒙特卡洛运行时的实际位置，移动步数T=100，蒙特卡洛运行次数MC=1 000。当NLOS误差服从高斯分布时，具体参数如表1所示。

显示原图|下载原图ZIP|生成PPT

图2 仿真轨迹图

表1 高斯分布仿真实验参数

参数名称	符号	参数值
信标节点数量	N	6
视距误差分布	$N 0, σ L 2$	$N 0, 12$
非视距概率	$Γ N L O S$	0.5
非视距误差分布	N（ $μ N L O S, σ 2 N L O S)$	$N 5, 62$

从图3中可以看出，随着NLOS概率的增加，6种算法的定位误差呈上升趋势，但本文算法（IMM-MEFPDAF）定位精度始终都是最高的。在非视距误差的概率很低时，本文算法和MJPDA的定位误差非常接近，但随着非视距误差的不断增加，本文算法的优势更加明显。

显示原图|下载原图ZIP|生成PPT

图3 不同的非视距误差概率情况下RMSE值

图4反映了当标准差从3增加到10时，均方根误差（RMSE）的变化趋势。很明显，本文算法和MJPDA的变化都较为平缓，其他4种算法的误差的上升幅度比较大，并且本文算法定位精度一直都是最高的。

显示原图|下载原图ZIP|生成PPT

图4 不同的标准差情况下RMSE值

图5反映当平均值从1增加到7时，各个算法的均方根误差变化情况。虽然本文算法的均方根误差有所增加，但是始终小于其他算法。本文算法的定位精度相较于MJPDA、RIMM、IMM-EKF、REKF、EKF分别增加了5.36%、22.25%、24.03%、39.68%、40.64%。

显示原图|下载原图ZIP|生成PPT

图5 不同非视距误差平均值下的RMSE值

在图6中，随着信标节点数量从4个增加到8个，6种算法的定位误差都在不断减小，这说明信标节点的数量越多，定位精度越高。MJPDA和本文算法定位误差减小得更明显一些，本文算法一直保持误差最小。当基站增加到8个时，MJPDA算法和本文算法定位精度几乎一致。

显示原图|下载原图ZIP|生成PPT

图6 不同的基站情况下RMSE值

通过1 000次蒙特卡洛模拟获得的CDF如图7所示。由图7可以看出，本文的定位误差是收敛最快的。此外，本文算法90%定位误差小于4.508 m。MJPDA、RIMM、IMM-EKF、REKF和EKF的90%的定位误差分别小于5.269、5.867、6.018、7.679和7.712 m。

显示原图|下载原图ZIP|生成PPT

图7 定位误差CDF

假设非视距误差服从指数分布，仿真实验参数如表2所示。

表2 指数分布仿真实验参数

参数名称	符号	参数值
信标节点数量	N	6
视距误差分布	$N 0, σ L 2$	$N 0, 12$
非视距概率	$Γ N L O S$	0.5
非视距误差分布	$E λ$	$E 8$

图8显示了当非视距误差服从指数分布时，非视距误差的概率增加对均方根误差（RMSE）的影响。EKF、REKF、IMM-EKF、RIMM、MJPDA和本文算法的平均定位精度分别为4.477、4.33、2.981、2.797、2.409、1.801 m。

显示原图|下载原图ZIP|生成PPT

图8 不同的非视距误差概率情况下RMSE值

图9为指数分布参数对EKF、REKF、IMM-EKF、RIMM、MJPDA和本文算法的RMSE的影响。EKF、REKF、IMM-EKF、RIMM、MJPDA和本文算法的平均定位精度分别为4.744、4.612、3.389、3.115、2.772、1.735 m。

显示原图|下载原图ZIP|生成PPT

图9 不同指数分布参数下RMSE值

图10显示了当NLOS误差服从指数分布时，EKF、REKF、IMM-EKF、RIMM、MJPDA和本文算法的RMSE随着信标节点的数量变化而变化的趋势。当信标节点增长到5个以上时，EKF、REKF、IMM-EKF、RIMM的均方误差减小的趋势变得缓慢，而MJPDA和本文算法在信标节点为6个以上时，均方根误差下降的速度变慢，信标节点增加到8个时，均方根误差基本一致。EKF、REKF、IMM-EKF、RIMM、MJPDA和本文算法的平均定位精度分别为5.89、5.723、4.414、4.182、3.641、2.556 m。本文算法定位精度分别比EKF、REKF、IMM-EKF、RIMM和MJPDA高56.60%、55.34%、42.00%、38.88%和29.79%。

显示原图|下载原图ZIP|生成PPT

图10 不同的基站情况下RMSE值

3.1.2 复杂度分析

本节通过程序的运行时间分析6种算法的运算复杂度。6种算法由MATLAB编程实现，运行平台为Windows10系统，计算机配置了 2.50 GHz的i5处理器，有8GB内存。

程序运行时间由MATLAB TIC TOC函数进行计算，该函数为MATLAB系统内置函数，通过在程序首尾分别写入tic和toc标记，软件可记录在两标记间的程序运行所花费的时间。

表3列出了各个算法平均定位一次所需要的时间。

表3 算法运行时间

算法名称	运行时间/s
EKF	0.000 096
REKF	0.000 136
IMM-EKF	0.000 192
RIMM	0.000 307
MJPDA	0.004 821
本文	0.003 540

由表3可以看出，扩展卡尔曼滤波有最短的运行时间，这是因为扩展卡尔曼滤波的迭代结构最简单，其拥有最低的算法复杂度。尽管本文算法运行时间相比于传统的经典算法较长，但是本文算法在精度上有很大的提高。相比于近几年的研究热点MJPDA，本文算法运行时间也占据优势。

3.2 实验

为了证明本文算法的有效性，在真实的室内场景中设计了一个实验。实验的地点安排在一个16.5 m×8 m的教室里，如图11所示。将6个基站的位置设置为

x 1 = 1.2 m, y 1 = 3.6 m 、

x 2 = 3.3 m, y 2 = 0.6 m 、 x 3 = 5.4 m, y 3 = 4.2 m 、 x 4 = 9.1 m, y 4 = 1.2 m 、 x 5 = 9.6 m, y 5 = 3.6 m 、

x 6 = 11.4 m, y 6 = 5.2 m 。

显示原图|下载原图ZIP|生成PPT

图11 实验场景平面图

虚线表示MN的移动轨迹，它沿着箭头的方向从教室到走廊，最后回到教室。采用UWB获取MN和BN之间的距离，它具有传输速度快、传输功率低、穿透能力强、定位精度高等优点^［17］。总共设置30个采样点，每个采样点间隔时间为1 s，取平均值作为最终结果。

每个采样点的误差分布如图12所示，定位误差的CDF如图13所示。从图12可以看出，在大多数情况下，本文算法的定位性能优于EKF、REKF、IMM-EKF、RIMM和MJPDA。通过图13计算得到，本文算法的90%的定位误差小于1.087 m，相比之下，EKF、REKF、IMM-EKF、RIMM和MJPDA的定位误差分别为1.844、1.933、1.776、1.632、1.572 m。

显示原图|下载原图ZIP|生成PPT

图12 样本点的定位误差

显示原图|下载原图ZIP|生成PPT

图13 定位误差的CDF

4 结论

本文提出了一种改进的基于到达时间的最大熵模糊概率数据关联算法。采用分组的思想将N个测量值分为L组，每组通过IMM-EKF获得相应的移动节点位置估计、模型概率和协方差矩阵，之后将得到的L个位置估计通过验证门进行非视距检测，在验证门外的被丢弃，利用相应的关联概率对正确的位置估计进行加权，并利用最大熵概率数据关联算法，其能够在计算复杂度很低的情况下实现更准确的位置估计。仿真和实验结果表明，与现有的算法EKF、REKF、IMM-EKF、RIMM、MJPDA相比，本文算法可以减轻非视距误差带来的影响，实现更高的定位精度。

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Kim J.Non-line-of-sight error mitigating algorithms for transmitter localization based on hybrid TOA/RSSI measurements［J］.Wireless Networks，2020，26（5）：3629-3635.

2	Kim J.Suppression of NLOS errors in TDOA-AOA hybrid localization［J］.Wireless Networks，2023，29（2）：657-667.

3	Sun Y H， Yang S L， Wang G，et al.Robust RSS-based source localization with unknown model parameters in mixed LOS/NLOS environments［J］.IEEE Transactions on Vehicular Technology，2021， 70（4）：3926-3931.

4	Monfared S， Pocoma E， Doncker P，et al.AOA-based iterative positioning of IOT sensors with anchor selection in NLOS environments［J］.IEEE Transactions on Vehicular Technology，2021，70（6）：6211-6216.

5	Liu J， Wang Z H， Cui J H，et al.A joint time synchronization and localization design for mobile underwater sensor networks［J］.IEEE Transactions on Mobile Computing，2015，15（3）：530-543.

6	Hammes U， Zoubir A M.Robust MT tracking based on M-estimation and interacting multiple model algorithm［J］.IEEE Transactions on Signal Processing，2011，59（7）：3398-3409.

7	Kirubarajan T， bar-shalom Y.Probabilistic data asso-ciation techniques for target tracking in clutter［J］.Proceedings of the IEEE，2004，92（3）：536-557.

8	Hammes U， Zoubir A M.Robust mobile terminal tracking in NLOS environments based on data asso-ciation［J］.IEEE Transactions on Signal Processing，2010，58（11）：5872-5882.

9	Fortmann T， Bar-Shalom Y， Scheffe M.Sonar tracking of multiple targets using joint probabilistic data association［J］.IEEE Journal of Oceanic Engineering，1983，8（3）：173-184.

10	He S M， Shin H S， Tsourdos A.Joint probabilistic data association filter with unknown detection probability and clutter rate［J］.Sensors，2018，18（1）：269.

11	Cheng L， Li Y F， Xue M K，et al.An indoor localization algorithm based on modified joint probabilistic data association for wireless sensor network［J］.IEEE Transactions on Industrial Informatics，2021，17（1）：63-72.

12	Zhou M， Li Y， Tahir M J， et al. Integrated Statistical test of signal distributions and access point contributions for Wi-Fi indoor localization［J］.IEEE Transactions on Vehicular Technology，2021，70（5）： 5057-5070.

13	Han K， Xing H S， Deng Z L，et al.A RSSI/PDR-based probabilistic position selection algorithm with NLOS identification for indoor localisation［J］.ISPRS International Journal of Geo-Information，2018，7（6）：232.

14	Zhu Y H， Ma T F， Li Z J，et al.NLOS identification and correction based on multidimensional scaling and quasi-accurate detection［J］.IEEE Access，2019（7）：53977-53987.

15	Mendrzik R， Bauch G.Position-constrained stochastic inference for cooperative indoor localization［J］. IEEE Transactions on Signal and Information Processing over Networks， 2019，5（3）： 454-468.

16	Barral V， Escudero C J， García-Naya J A，et al.NLOS identification and mitigation using low-cost UWB devices［J］.Sensors，2019，19（16）：3464.

17	Ridolfi M， Kaya A， Berkvens R，et al.Self-calibration and collaborative localization for UWB positioning systems：a survey and future research directions［J］.ACM Computing Surveys，2021，54（4）：1-27．

Options

Outlines

模态框（Modal）标题

Abstract

Cite this article

1 信号模型搭建

2 定位跟踪算法

2.1 总体思想

图1 算法结构图

2.2 分组和IMM-EKF估计

2.3 最大熵模糊概率数据关联算法

2.3.1 卡尔曼滤波

2.3.2 非视距识别

2.3.3 最大熵模糊概率数据关联

3 仿真和实验

3.1 仿真

3.1.1 定位精度分析

图2 仿真轨迹图

表1 高斯分布仿真实验参数

图3 不同的非视距误差概率情况下RMSE值

图4 不同的标准差情况下RMSE值

图5 不同非视距误差平均值下的RMSE值

图6 不同的基站情况下RMSE值

图7 定位误差CDF

表2 指数分布仿真实验参数

图8 不同的非视距误差概率情况下RMSE值

图9 不同指数分布参数下RMSE值

图10 不同的基站情况下RMSE值

3.1.2 复杂度分析

表3 算法运行时间

3.2 实验

图11 实验场景平面图

图12 样本点的定位误差

图13 定位误差的CDF

4 结论

References