Flutter characteristics of supersonic cantilever plate with embedded mass

Wuchao QI; Haoyang YU; Sumei TIAN; Hongliang LIU

doi:10.3969/j.issn.2095-1248.2024.02.001

Journal of Shenyang Aerospace University >

2024 , Vol. 41 >Issue 2: 1 - 13

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.02.001

Aerospace Engineering

Flutter characteristics of supersonic cantilever plate with embedded mass

Wuchao QI ,
Haoyang YU ,
Sumei TIAN ,
Hongliang LIU

Expand

Key Laboratory of Liaoning Province for Composite Structural Analysis of Aircraft and Simulation，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2023-12-14

Online published: 2024-05-29

Fold

Abstract

In order to improve the flutter velocity of a lifting surface with embedded mass，the lifting surface was simplified as a rectangular cantilever plate with concentrated mass.Based on the assumed mode method and the first-order piston theory，a flutter model was obtained，and flutter characteristics of the rectangular cantilever plate were investigated.Firstly，the structural dynamic model of the rectangular cantilever plate was established based on the Kirchhoff thin plate theory，and the modal properties of the plate with embedded mass were obtained using the assumed mode method； secondly，the first-order piston theory was introduced to approximate the modal aerodynamic force under supersonic conditions，and the time-domain expression of the flutter equation was obtained by substituting it into the structural dynamics model； finally，the flutter equation was transformed into the frequency domain by introducing the modal displacement in exponential form and the flutter velocities and flutter frequencies were solved by the p-k method.By changing the position，mass，number and other parameters of embedded objects，the law of their influence on the flutter characteristics of the supersonic cantilever plate was obtained.The results show that the flutter velocity of the lifting surface can be effectively increased by embedding small mass objects near the leading edge of the cantilever plate near the wing tip，and the flutter velocity is insensitive to the change of the embedded mass near the wing root.

Key words： flutter; embedded mass; piston theory; the assumed mode method; supersonic cantilever plate

Cite this article

Wuchao QI , Haoyang YU , Sumei TIAN , Hongliang LIU . Flutter characteristics of supersonic cantilever plate with embedded mass[J]. Journal of Shenyang Aerospace University, 2024 , 41(2) : 1 -13 . DOI: 10.3969/j.issn.2095-1248.2024.02.001

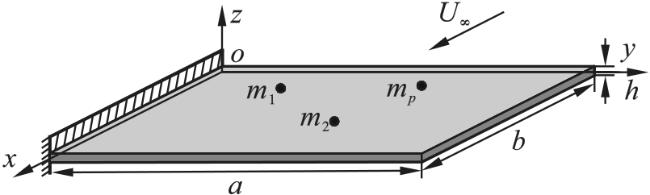
超声速飞行器的飞行速度包线受到来自结构、气动和控制等方面的共同制约。随着飞行速度的不断增大，飞行器结构会从气流中不断汲取能量而发生振动。当飞行速度达到某一数值时，升力面将维持一种等幅振荡状态，此时的飞行速度被认为是颤振边界。颤振是一种危险的行为，飞行器结构可能会在数秒内发生解体。另一方面，设计先进飞行器时，通常希望其工作于多任务剖面，需要携带的质量附着物也是多样的，例如弹体、主（副）油箱、自毁装置等。同时，为了不影响升力面的气动外形，这些装置通常以内埋形式置于机翼和机身内部。所以，对带内埋质量机翼颤振特性的研究是迫切的。

2003年，Chiba等^［1］采用Rayleigh-Ritz法对附加有弹簧-质量系统的悬臂薄板进行了耦合自由振动分析，阐明了附加质量、弹簧常数及附加系统位置对系统耦合振动特性的影响。之后，赵永辉^［2-3］详细研究了超声速悬臂板及超声速翼面颤振的分析方法。肖艳平等^［4］研究了复合材料机翼的颤振速度随材料耦合刚度的变化及在不同挂载刚度、挂载位置情况下颤振速度随材料耦合刚度的变化。陈晓明等^［5］结合理论分析、数值模拟及实验测量计算了含有集中质量悬臂薄板模型的固有频率，经过对比发现三者有较好的一致性。Aksencer等^［6］使用Ritz法研究了带有附加点质量的旋转层压复合梁的自由振动。Rahmane等^［7］研究了在夹紧/自由边界条件的弯曲振动下，附加质量对复合材料层合板动态特性的影响，并得到了质量大小对固有频率的影响。Pacheco等^［8］采用非线性能量阱来抑制面板颤振并降低极限循环振荡的强度，探究了非线性能量阱的参数如何影响气动弹性响应的本质。Molina等^［9］提出了一种带附加质量的矩阵计算方法，在颤振计算中可有效地提升准确性和计算效率。Bera等^［10］使用可控小翼和旋转质量阻尼器的组合进行了桥面的颤振抑制，桥面在颤振时的垂直响应可通过旋转质量阻尼器进行有效衰减。Zhou等^［11-12］尝试使用非线性能量阱（nonlinear energy sink，NES）来抑制面板颤振，利用Galerkin方法建立了超声速流动中具有NES的二维平板的非线性气动弹性模型。Tian等^［13］设计了一个嵌入局部非线性谐振器的周期性阵列的超材料板，与非超材料板进行比较，证明其有更高的颤振边界和更低的振幅。Bahrami等^［14］提出了一种新型流固耦合有限元模型来研究超声速流动下矩形板的动态稳定性，对具有不同几何特性和边界条件的矩形板进行了计算。祁武超等^［15］基于假设模态法提出一种带集中质量弯扭组合梁模态分析手段，结合片条理论考察了外挂物不同质量及位置分布对机翼颤振的影响。Qi等^［16］用假设模态法求得附着集中质量壁板的模态函数，使用一阶活塞理论和p - k法，对不同质量附着的情况进行颤振分析，预测有质量附着时壁板的颤振速度。Tian等^［17］提出了一种罚函数的刚度矩阵约束关系处理方法，结合一阶活塞理论计算了不同弹性支撑边界条件的薄壁板的颤振特性，并通过增加阻尼来对颤振速度进行增强和恢复。Muñoz等^［18］提出了一种计算亚声速、跨声速和超声速势流中机翼截面在拉普拉斯域下的非定常气动力求解方法，对三自由度机翼截面的主动颤振抑制进行研究，得到了合适的控制方法。Uymaz^［19］使用三维Ritz解分析了质量和温度对任意位置承载点质量的功能梯度板的自由振动的影响。Kalosha等^［20］考虑了一个带有附加弹簧质量系统的简支欧拉-伯努利梁的数学模型，该模型由分布式压电致动器和集中力控制。Dadoulis等^［21］研究了在外部基础运动下具有大质量附件梁的解析解。Mahmoud^［22］介绍了使用集中质量传递矩阵对承载任意数量质量点的非均匀和阶梯式轴向功能梯度梁进行自由振动分析的方法。Simiriotis等^［23］介绍了直接预测法、在频域内求解的p - k法和有理插值法等3种方法求解颤振方程，所预测的颤振速度几乎相同。

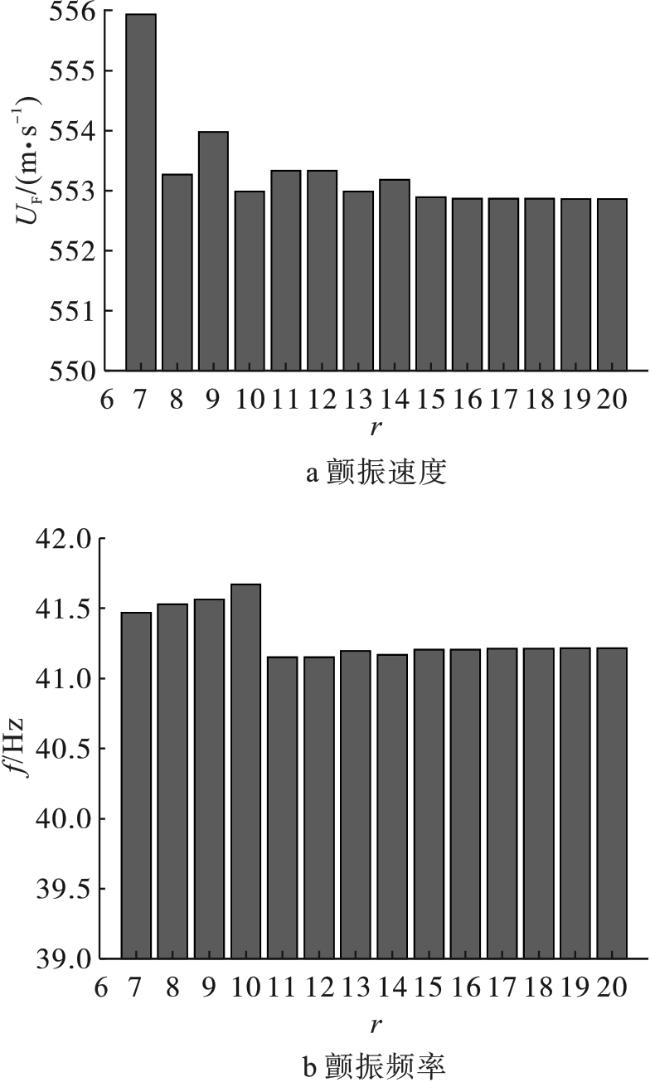
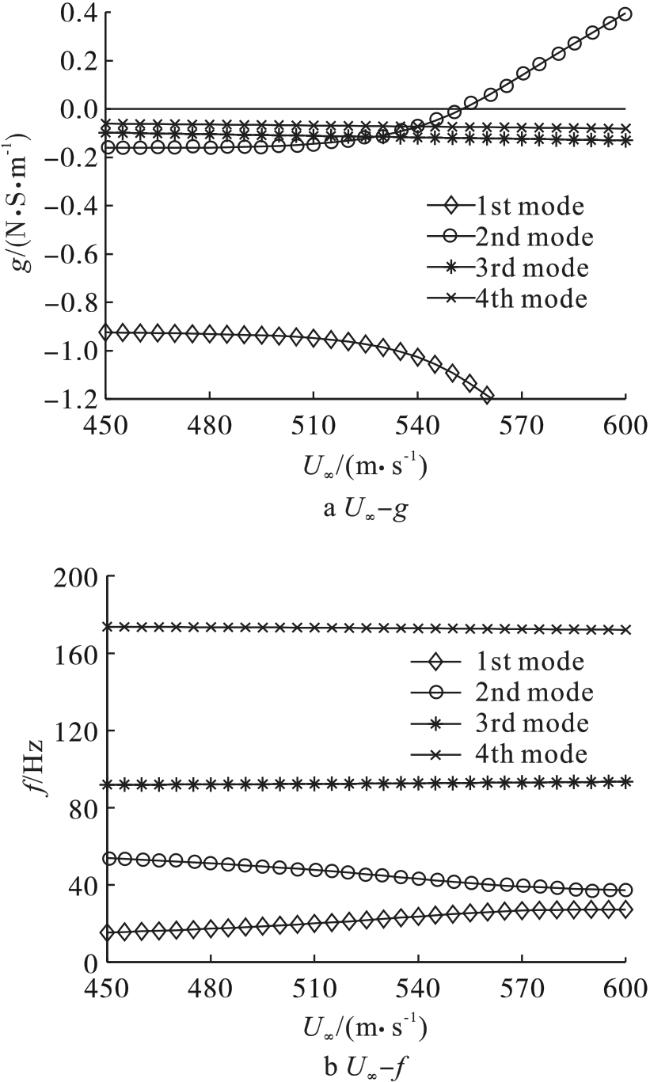
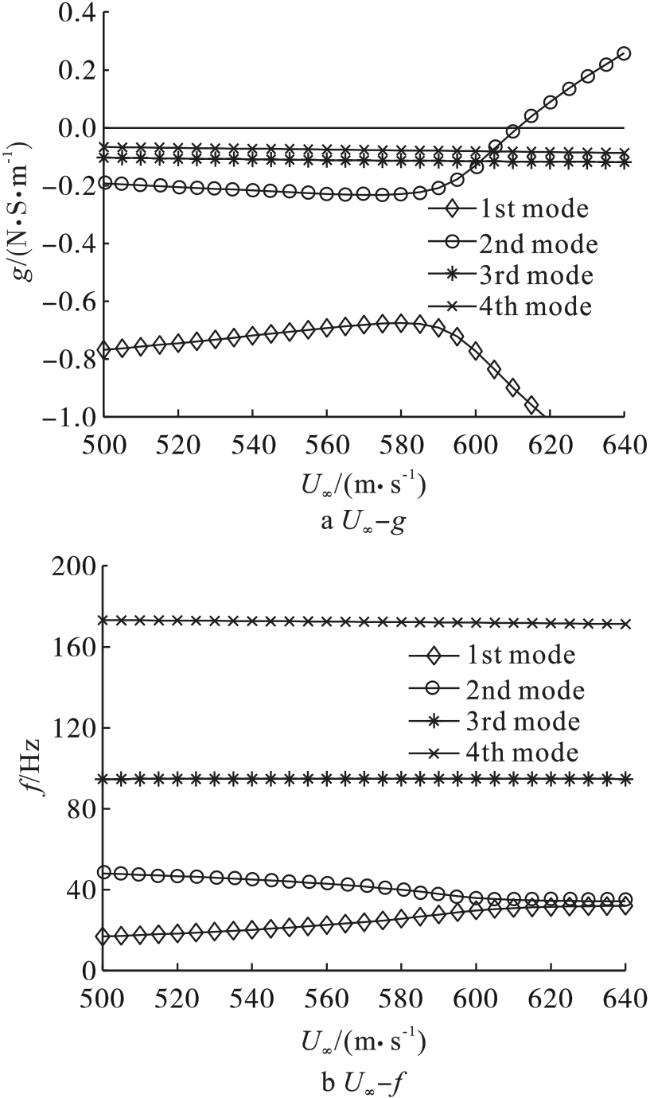
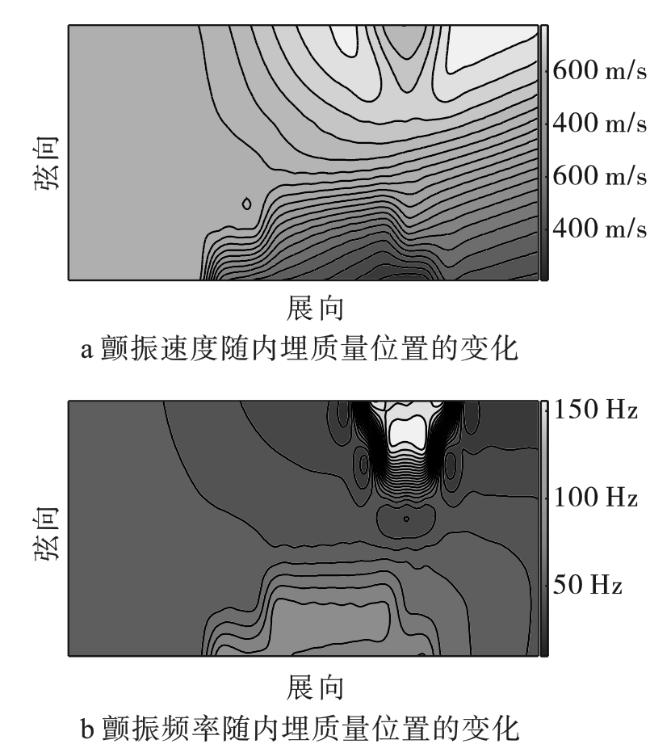
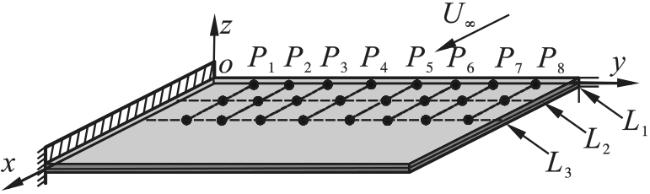
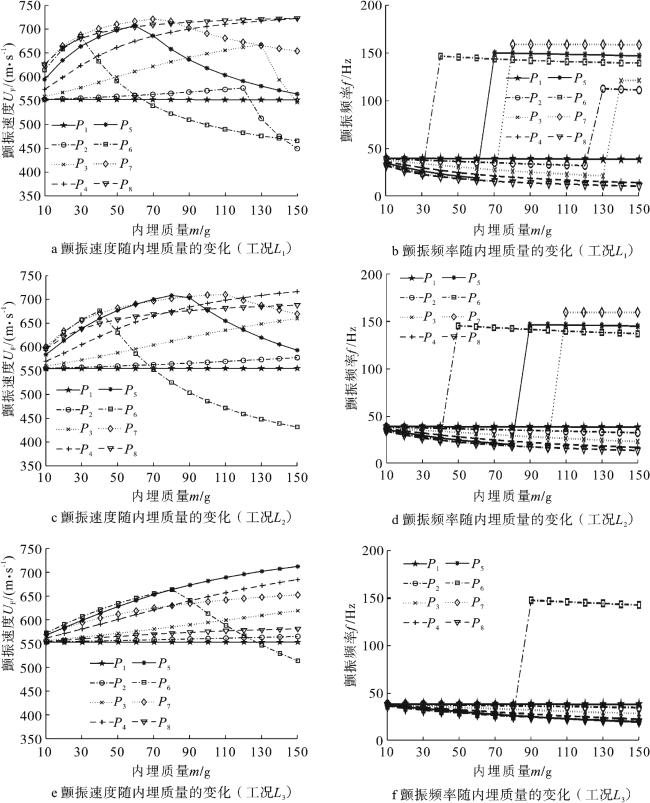
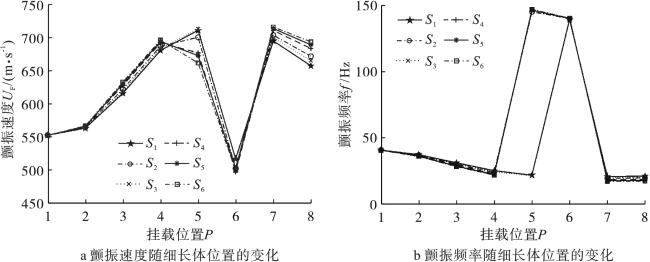
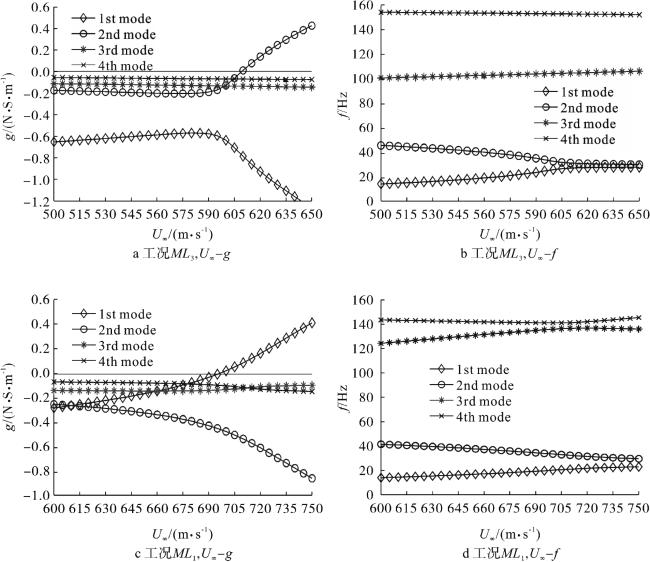
现有文献主要研究了附加质量对板自由振动特性的影响，而在讨论附加质量对板颤振特性影响方面仍处于起步阶段，尤其是具有多质量附着时板的颤振特性方面未见相关研究成果。另外，在初始设计过程中，需要不断考察板的尺寸效应及内埋件质量属性的变化（大小、位置、数目等因素）所带来的效应，重复建立有限元模型，并利用Nastran进行分析，从而产生极大的计算代价和时间成本。从解析的角度构建气动弹性模型则具有明显优势，一方面可以有效地提高计算效率，另一方面则更容易观察质量参数变化对系统本质属性的影响。因此，本文基于假设模态法得到带内埋质量矩形板的模态特性，并结合一阶活塞理论求解悬臂板的颤振分析模型，通过改变内埋件位置、质量大小和数目等参数，分析其对超声速悬臂板颤振特性的影响规律。

1 带内埋质量悬臂板的颤振方程

考察如图1所示的带内埋质量悬臂板的几何模型，展向和弦向的长度分别为a和b，板厚为h，这里h远小于a和b，即所考虑的悬臂板为薄板。在所建立的全局坐标系中，坐标原点o位于靠近固定端的前缘处，x轴正向为顺气流方向，y轴正向为悬臂板展向方向，z轴正向为悬臂板的法线方向（右手坐标系）。悬臂板在超声速气流中运动，相对来流速度记为

U ∞

。板面内附着有N_p 个内埋件，可将其等效为集中质量，其中第p个内埋件的质量记为m_p，挂载点记为（x_p，y_p，z_p ）。由于附加质量的内埋属性和悬臂板的薄板特征，这里可忽略内埋件z向坐标的变化所带来的影响。

显示原图|下载原图ZIP|生成PPT

图1 带内埋质量悬臂板的几何模型

由于内埋质量件的存在，悬臂板的质量属性发生了比较大的变化，相应地其固有特性也会发生改变。本文引入假设模态法以得到带内埋质量悬臂板的模态属性。基于Kirchhoff薄板理论，悬臂板的弯曲势能可写为

U B = D b 2 ∫ 0 a ∫ 0 b ∂ 2 w ∂ x 2 2 + ∂ 2 w ∂ y 2 2 d x d y + D b ∫ 0 a ∫ 0 b ν ∂ 2 w ∂ x 2 ∂ 2 w ∂ y 2 + 1 - ν ∂ 2 w ∂ x ∂ y 2 d x d y

（1）

式中：D_b 为板的抗弯刚度；w为板的弯曲变形；

ν

为泊松比。

T _B和T _A分别为悬臂板发生振动时自身动能附加质量件的动能，则系统的总动能为

T = T B + T A = 12 ∫ 0 a ∫ 0 b ρ h ∂ w ∂ t 2 d x d y + 12 ∑ p = 1 N p m p ∂ w x p, y p, t ∂ t 2

（2）

式中：

ρ

为悬臂板的质量密度。

取带内埋质量悬臂板的假设模态为

ψ ˜ i x, y = ϕ m x φ n y, m = 1,2, ⋯, N m; n = 1,2, ⋯, N n

（3）

式中：

ϕ m x

和

φ n y

分别为两端自由梁和悬臂梁的振型函数；变量i根据

ϕ m

和

φ n

组合得出的悬臂板固有频率的大小来排序，具体表达式为^［4］

ϕ m x = 2, m = 1 2 1 - 2 x / b, m = 2 R + S, m ≥ 3

（4）

其中

R = c o s h β m x / b + c o s β m x / b S = σ m s i n h β m x / b + s i n β m x / b

（5）

其中

β m = 4.73, m = 3 7.853, m = 4 m - 3 / 2 π, m ≥ 5

（6）

σ m = - c o s h β m - c o s β m s i n h β m - s i n β m

（7）

φ n y = c o s h β n y / a - c o s β n y / a + σ n s i n h β n y / a - s i n β n y / a

（8）

其中

β n = 1.875, n = 1 4.694, n = 2 n - 1 / 2 π, n ≥ 3

（9）

σ n = - c o s h β n + c o s β n s i n h β n + s i n β n

（10）

基于式（3），悬臂板的z向位移函数

w x, y, t

可写为

w x, y, t = ∑ i = 1 r ψ ˜ i x, y q i t

（11）

式中：

q i t

为系统第i阶主坐标；r为模态截断阶数。将式（11）代入式（1），可将系统势能改写为

U = 12 ∑ i = 1 r ∑ j = 1 r k ˜ i j q i t q j t

（12）

其中

k ˜ i j = D b ∫ 0 a ∫ 0 b ∂ 2 ψ ˜ i ∂ x 2 ∂ 2 ψ ˜ j ∂ x 2 + ∂ 2 ψ ˜ i ∂ y 2 ∂ 2 ψ ˜ j ∂ y 2 d x d y + 2 D b ∫ 0 a ∫ 0 b ν ∂ 2 ψ ˜ i ∂ x 2 ∂ 2 ψ ˜ j ∂ y 2 + 1 - ν ∂ 2 ψ ˜ i ∂ x ∂ y ∂ 2 ψ ˜ j ∂ x ∂ y d x d y

（13）

同时，将式（11）代入式（2），可将系统动能改写为

T = 12 ∑ i = 1 r ∑ j = 1 r m ˜ i j q ˙ i t q ˙ j t

（14）

其中

m ˜ i j = ρ h ∫ 0 a ∫ 0 b ψ ˜ i x, y ψ ˜ j x, y d x d y + ∑ p = 1 N p m p ψ ˜ i x p, y p ψ ˜ j x p, y p

（15）

由式（13）和式（15）得出带内埋质量悬臂板的广义刚度矩阵

K ˜ = k ˜ i j r × r

和广义质量矩阵

M ˜ = m ˜ i j r × r

，将其代入本征方程，有

K ˜ - ω 2 M ˜ = 0

（16）

可得到系统的前r阶固有频率

ω 1, ω 2, ⋯, ω r

和特征向量

a 1, a 2, ⋯, a r

，写成矩阵形式为

Φ = a 1, a 2, ⋯, a r

（17）

记为

ψ = ψ 1, ⋯, ψ r

（18）

则

ψ

与假设模态

ψ ˜ = ψ ˜ 1, ⋯, ψ ˜ r

之间存在着变换关系，可写为

ψ = ψ ˜ Φ

（19）

因此，带内埋质量悬臂板的第i阶模态可写为

ψ i x, y = ∑ j = 1 r ψ ˜ j x, y a j i

（20）

利用式（20）可以得到带内埋质量悬臂板系统的位移函数为

w x, y, t = ∑ i = 1 r ∑ j = 1 r ψ ˜ j x, y a j i q i t

（21）

引入主质量参数为

M i i = ∫ 0 a ∫ 0 b ρ h ψ i x, y 2 d x d y = ∫ 0 a ∫ 0 b ρ h ∑ j = 1 r ψ ˜ j x, y a j i 2 d x d y

（22）

主刚度参数为

K i i = D b ∫ 0 a ∫ 0 b ∂ 2 ψ i ∂ x 2 ∂ 2 ψ i ∂ x 2 + ∂ 2 ψ i ∂ y 2 ∂ 2 ψ i ∂ y 2 d x d y + 2 D b ∫ 0 a ∫ 0 b ν ∂ 2 ψ i ∂ x 2 ∂ 2 ψ i ∂ y 2 + 1 - ν ∂ 2 ψ i ∂ x ∂ y ∂ 2 ψ i ∂ x ∂ y d x d y

（23）

由于悬臂板的刚度属性并没有因为附加的内埋质量而发生改变，所以，主刚度参数

K i i

也可以被改写为

K i i = D b ∫ 0 a ∫ 0 b ∂ 2 ψ ˜ i ∂ x 2 ∂ 2 ψ ˜ i ∂ x 2 + ∂ 2 ψ ˜ i ∂ y 2 ∂ 2 ψ ˜ i ∂ y 2 d x d y + 2 D b ∫ 0 a ∫ 0 b ν ∂ 2 ψ ˜ i ∂ x 2 ∂ 2 ψ ˜ i ∂ y 2 + 1 - ν ∂ 2 ψ ˜ i ∂ x ∂ y ∂ 2 ψ ˜ i ∂ x ∂ y d x d y

（24）

则系统的第i阶固有频率为

ω i = K i i M i i, i = 1,2, ⋯, r

（25）

忽略系统的结构阻尼，可以得到用模态坐标表示的系统运动方程为

M i i q ¨ i t + K i i q i t = Q i t, i = 1,2, ⋯, r

（26）

其中

Q i

为第i阶模态气动力，需要通过作用在悬臂板上的气动条件得到，式（26）的矩阵形式为

M q ¨ (t) + K q ˙ (t) = Q (t)

（27）

基于一阶活塞理论求解超声速条件下悬臂板上的模态气动力。由于所考虑的悬臂板为等厚度的，板的厚度函数关于顺气流方向的梯度为0，所以可以忽略板厚对上下表面压差的影响。

对于悬臂板上表面内的点，其

z

向速度为

v z U = U ∞ ∂ ∂ x + ∂ ∂ t w x, y, t = U ∞ ∂ ∂ x + ∂ ∂ t ∑ i = 1 r ∑ j = 1 r ψ ˜ j x, y a j i q i (t)

（28）

而对于下表面，有

v z L = - U ∞ ∂ ∂ x + ∂ ∂ t w x, y, t = - U ∞ ∂ ∂ x + ∂ ∂ t ∑ i = 1 r ∑ j = 1 r ψ ˜ j x, y a j i q i (t)

（29）

利用式（28）和（29），悬臂板下表面与上表面的压差系数

Δ p x, y, t

为

Δ p (x, y, t) = - 4 q d M a ∞ ∑ i r ∑ j r ∂ ψ ˜ j x, y ∂ x a j i q i (t) ∂ w ∂ x + 1 U ∞ ∑ i r ∑ j r ψ ˜ j x, y a j i q ˙ i (t)

（30）

式中：

q d

为动压，

q d = ρ ∞ U ∞ 2 / 2

；

M a ∞

为未扰动空气的马赫数。将系统的位移函数带入式（30）中，得到第i阶模态气动力

Q i (t) = ∫ 0 a ∫ 0 b Δ p x, y, t ψ i x, y d x d y = - 4 q d M a ∞ ∑ j = 1 r D ¯ i j q j (t) + 1 U ∞ E ¯ i j q ˙ j (t)

（31）

式中

D ¯ i j = ∫ 0 a ∫ 0 b ∑ s = 1 r ψ ˜ s x, y a s i ∑ s = 1 r ∂ ψ ˜ s x, y ∂ x a s j d x d y

（32）

E ¯ i j = ∫ 0 a ∫ 0 b ∑ s = 1 r ψ ˜ s x, y a s i ∑ s = 1 r ψ ˜ s x, y a s j d x d y

（33）

从式（31）可以看出，作用在悬臂板上的气动力系数被分成了两部分：一部分为

q j (t)

前面的系数

D ¯ i j

，起到气动刚度的作用；另外一部分为

q ˙ j (t)

前面的系数

E ¯ i j

，起到气动阻尼的作用。

将式（31）代入式（26）中，可得到带内埋质量悬臂板颤振方程的时域表达形式为

M i i q ¨ i t + K i i q i t = - 4 q d M a ∞ ∑ j = 1 r D ¯ i j q j (t) + 1 U ∞ E ¯ i j q ˙ j (t), i = 1,2, ⋯, r

（34）

式（34）的矩阵形式为

M q ¨ (t) + K q ˙ (t) = q d - 4 M a ∞ D ¯ q (t) + 1 U ∞ E q ˙ (t)

（35）

2 颤振分析

当颤振发生时，系统作谐振荡运动。p-k法将被引入以在频域内求解式（35）所示的颤振方程。为此，模态位移向量

q t

被重写为

q t = q ¯ e s t

（36）

式中：

q ¯

是

q t

的振幅，与时间无关；

s = γ + i ω

，

γ

是瞬态衰减率系数，它决定了振动衰减的速度。引入无量纲参数

p = γ + 1 k

（37）

式中：k为系统缩减频率。式（36）可以被重写为

q t = q ¯ e p U ∞ b t

（38）

将式（38）代入到式（35）中，可以得到

2 U ∞ b 2 M p 2 + K - 2 q d Q k, M a ∞ q ¯ = 0

（39）

式中：

Q k, M a ∞ = - 4 M a ∞ D ¯ + 2 p a E ¯

，为了便于计算，把

Q k, M a ∞

分为实部和虚部两部分。

Q k, M a ∞ = Q R e k, M a ∞ + i Q I m k, M a ∞

（40）

于是颤振方程可改写为

2 U ∞ a 2 M p 2 + K - 2 q d Q R e k, M a ∞ - i 2 q d Q I m k, M a ∞ q ¯ = 0

（41）

将式（41）中

i 2 q d Q I m k, M a ∞

改写为

i 2 q d Q I m k, M a ∞ = 2 q d Q I m k, M a ∞ k p

（42）

显然，式（42）只有

γ = 0

等号才严格成立

记

A ¯ = 2 U ∞ b 2 M B ¯ = - q d Q I m k, M a ∞ k C ¯ = K - q d Q R e k, M a ∞

（43）

可以得到带内埋质量悬臂板颤振系统的二次特征值问题为

A ¯ p 2 + B ¯ p + C ¯ q ¯ = 0

（44）

式中：参数p的计算需要迭代进行。当系统收敛到当前流速

U ∞

时，可以得到人工结构阻尼g和频率f的计算式为

g ≈ 2 γ = 2 R e p k

（45）

f = k U ∞ b π

（46）

3 数值算例

对于超声速流中的悬臂板系统，其物理参数如表1所示。当系统在海平面附近飞行时，进行颤振计算的空气参考密度

ρ ∞ = 1.226

kg/m³，空气密度比为1.0。在类似机翼的气动弹性系统中，当系统处于颤振临界时，通常表现为气动阻尼占主导成分，而结构阻尼对气动弹性系统的影响较小。所以，为了清晰了解气动弹性系统的本质属性，在计算过程中忽略了结构阻尼，并给出偏于“保守”的设计方案。

表1 悬臂板的物理参数

物理参数	最大值
展长a/m	0.5
弦长b/m	0.1
板厚h/m	0.003
弹性模量E/Pa	7.1×10¹⁰
泊松比 $ν$	$0.32$
体密度 $ρ$ /（kg·m ^- ³）	$2 768$

图2为

M a ∞ = 2.0

时悬臂板颤振速度和颤振频率随模态截断数r的变化情况。由图2可知，为了得到收敛的颤振速度和颤振频率，至少应选取系统的前15阶固有模态参与颤振计算。为了保证计算精度，同时不增加额外的计算量，在后续的颤振计算过程中，均采用前16阶模态参与计算。

显示原图|下载原图ZIP|生成PPT

图2 颤振速度和颤振频率随模态截断数 r 的变化

取悬臂板的前16阶模态参与计算，忽略结构阻尼，在

M a ∞ = 2.0

的情况下利用本文所提方法计算得到非匹配的颤振速度和颤振频率，如图3所示。从图3可知，无内埋质量件的悬臂板系统颤振速度为552.71 m/s，颤振频率为41.25 Hz，颤振发生在第2阶模态。由图3b可知，当颤振发生时，第2阶模态趋向与第1阶模态发生耦合。

显示原图|下载原图ZIP|生成PPT

图3 无内埋质量情形下的颤振计算结果

为了验证本文所提出方法的准确性，使用MSC.Nastran软件计算了相同的问题，得到颤振速度为555.63 m/s，颤振频率为40.96 Hz。颤振速度和颤振频率分别相差0.53%和0.71%，计算结果误差控制在1%以内，验证了本文方法的正确性。

3.1 单个内埋集中质量的情形

首先考察在悬臂板中心点处布置内埋集中质量的情形。内埋质量件的质量

m p

为50 g（约是悬臂板质量的0.12倍），同样取前16阶模态参与颤振计算。由于有内埋质量的存在，悬臂板-质量系统的固有频率呈下降趋势。

基于本文所提方法计算了带集中质量悬臂板的颤振速度和颤振频率，如图4所示。从图4可知，悬臂板的颤振速度为611.39 m/s，颤振频率为34.97 Hz。相比无内埋质量的情形，颤振速度提升了58.68 m/s，上升比例为10.62%，而颤振频率则下降了6.28 Hz，下降比例为15.22%。颤振依然发生在第2阶模态，当颤振发生时，同样是第2阶模态与第1阶模态发生耦合，并且耦合程度变得更强。

显示原图|下载原图ZIP|生成PPT

**图4 颤振计算结果（ m_p = 0.05， x = b/2， y = a/2）**

对比无内埋质量和在悬臂板中心点内埋质量件的情形可以发现，系统的颤振特性发生了明显的变化。为进一步考察内埋质量的挂载位置对系统颤振速度的影响规律，分别在悬臂板上均匀选取156个挂载位置进行单个内埋集中质量的挂载，得到挂载位置对颤振速度和颤振频率随挂载位置变化的规律，如图5所示。

显示原图|下载原图ZIP|生成PPT

图5 不同挂载位置颤振计算结果

从图5a可知，在靠近翼根沿展向a/3范围内，颤振速度对内埋件位置的变化不明显，大约在1.7% 的范围内浮动，颤振也都发生在第2阶模态。在沿展向的同一站位，当内埋质量从前缘向后缘变化时，颤振速度会在某个位置发生突降，最大下降幅度可达到60%。当内埋质量沿展向变化时（中心线前的迎风区域），会出现颤振速度先增加再减小然后再增加的趋势，先后出现两次峰值。第一次峰值出现在沿展向约0.6a位置的前缘处，颤振速度为697.83 m/s，而第二次峰值出现在约0.8a位置的前缘处，颤振速度达到710.47 m/s。相较不带内埋质量的情形，颤振速度提高幅度达到28.54%。相较而言，在靠近后缘处布置内埋质量，会降低系统的颤振速度，尤其是在沿展向站位约0.7a处的后缘附近，颤振速度下降幅值达到最大。

而由图5b可知，除了将内埋质量布置在展向站位0.75 a附近的位置（靠近前缘处），颤振频率的变化对于内埋质量位置的变化整体上不敏感。在这个位置附近，颤振频率有一个突增，这是由于系统参数改变从而导致颤振模态发生了跳转。当悬臂板上的质量属性发生变化时，结构的模态属性会发生相应的变化，继而气动力也将重新分布。当质量参数（包括大小、数目和位置）变化至某个临界值时，所激发的颤振模态将会从原有模态跳转至其他模态。

由此可见，当只考虑单个内埋质量时，悬臂板面内存在两个较佳的挂载区域，即沿展向站位0.6a和0.8a附近的位置（靠近前缘处）。但值得注意的是，在这两者之间，有一个颤振速度的极小值点。

根据上述分析，位于悬臂板后缘的内埋质量会降低系统的颤振速度，所以不宜在此区域布置内埋件。基于此，仅考虑在悬臂板的前缘线L ₁、1/4弦线L ₂和悬臂板中心线位置上L ₃布置不同质量内埋件的情形，如图6所示。在不同的线上沿展向均匀选取8个位置，分别记为

P 1 ~ P 8

（不包含固定端和自由端）。

显示原图|下载原图ZIP|生成PPT

图6 内埋件在悬臂板面内的位置

考虑到悬臂板的承载能力，所考虑内埋件的质量在10~15 g 内变化，分别得到在工况L ₁~L ₃下悬臂板的颤振特性，如图7所示。

显示原图|下载原图ZIP|生成PPT

图7 悬臂板颤振特性随内埋质量的变化（工况 L ₁~L ₃ ）

由图7a可知，在前缘线上的不同挂点处，颤振速度会随着内埋质量的增大而出现变化。当内埋质量较小时，几乎所有情况下的颤振速度均有所增加。但随着内埋质量的增加，

P 2

、

P 3

、

P 5

、

P 6

、

P 7

均先后出现拐点，而最早出现拐点的是

P 6

。不同的是，

P 4

和

P 8

的颤振速度却是呈现单调递增趋势。而由图7b可知，除了

P 4

和

P 8

的颤振频率随着内埋质量的增加稍有降低外，其他挂点处的颤振频率均发生跃迁，这是由于颤振模态发生跳转所致。

由图7c可知，在悬臂板的1/4弦线上布置内埋质量，随着内埋质量的增大，除了

P 5

、

P 6

和

P 7

的颤振速度曲线有明显的拐点外，其余工况均随着内埋件质量的增大而提高或者维持较高的水平。这一点可以从图7d看出，

P 5

、

P 6

和

P 7

的颤振频率曲线在内埋质量达到某个值时发生了阶跃，同样是由于颤振模态发生跳转造成的。

当内埋质量点沿弦向后移至悬臂板中心线时（工况

L 3

），图7e显示除了

P 6

，其余内埋点的颤振速度曲线均随内埋质量的增加而单调递增，尤其以

P 5

的情形最佳。由图7f所示的颤振频率曲线可知，

P 6

在内埋质量为90 g 附近发生了模态跳转，而其余情形的颤振频率均随着内埋质量的增大而减小。

由以上分析可知，内埋件的挂载位置及质量大小会对系统颤振速度和颤振频率产生重要影响。适宜的挂载位置有两个区域，一个是靠近翼根的区域，在该区域挂载颤振速度和颤振频率对内埋件质量参数不敏感；另一个区域是在靠近翼梢从悬臂板中心线附近到前缘之间的位置，当在此区域挂载时，除了

P 6

附近区域，颤振速度均有大幅提升。然而，当在悬臂板展向中心线后缘方向挂载时，颤振速度则通常呈现下降趋势。

3.2 细长体的情形

当内埋件表现为细长体（沿弦向分布）时，通常使用2~3个挂点与悬臂板面连接。一般将细长体的挂点取为3个，并将其质量属性向该3个挂点进行简化。取细长体总质量为100 g，提出了6个质量分配方案，分别为S ₁~S ₆，如表2所示。

表2 细长体质量分配方案 (g)

方案	m ₁	m ₂	m ₃
S ₁	20	30	50
S ₂	20	50	30
S ₃	30	20	50
S ₄	30	50	20
S ₅	50	20	30
S ₆	50	30	20

根据3.1节的分析可知，为了保证挂载内埋质量件后，颤振速度不低于原有水平，应尽可能选择悬臂板中心线前的迎风区域进行挂载。所以，选取内埋质量的挂载点与图6所示的位置类似，即将细长体的3个挂点分别设置为

P i, (i = 1,2, ⋯, 8)

情形下的3个点，分别为前缘点、1/4弦线点和中心线点。需要注意的是3.1节中的情形是只有内埋质量点，而这里是沿弦向同时有3个简化的集中质量点。

将细长体所在位置由翼根逐步移至翼梢区域，系统的颤振特性发生了明显的变化，6种质量分配方案下的颤振速度和颤振频率曲线如图8所示。由图8可知，随着细长体挂载位置的展向变化，所有的颤振速度图像均呈现出两次峰值，即在

P 4

或

P 5

及

P 7

的位置，而

P 4

则为颤振速度曲线的陡降点，在此区域不宜布置内埋质量。不同质量分配方案下悬臂板的颤振速度和颤振频率曲线均具有类似的变化趋势，颤振速度的最大差异控制在7.0%左右。

显示原图|下载原图ZIP|生成PPT

图8 不同质量分配方案下内埋细长体悬臂板的颤振特性

3.3 多个内埋集中质量的情形（展向布置）

对于沿展向布置多个内埋集中质量的情形，一般考虑沿悬臂板展向均匀选取8个点进行挂载，如图6中沿

L i (i = 1,2, 3)

的8个点所示。内埋件总质量控制在100 g以内，均匀分布在8个点上。以悬臂板中心线的情形为例，记为工况ML ₃，绘制了

U ∞ - g

图和

U ∞ - f

图，如图9a、9b所示。

显示原图|下载原图ZIP|生成PPT

图9 颤振计算结果

由图9a、9b可知，悬臂板的颤振速度为609.47 m/s，相应的颤振频率为32.03 Hz，颤振发生在第2阶模态，为第1阶模态和第2阶模态耦合所致。相比未带内埋质量的情形，颤振速度提升了10.27%，而颤振频率则下降了22.35%。

然而，与此情形不同的是，当内埋件位置向前缘靠近时，颤振模态可能会发生跳转。考虑工况ML ₁情形，绘制了

U ∞ - g

图和

U ∞ - f

图，如图9c、9d所示。由图9c、9d可知，悬臂板颤振速度为695.17 m/s，颤振频率为19.51 Hz。颤振发生在第1阶弯曲模态，为第2阶模态与第1阶模态耦合所致，但同时第3阶模态和第4阶模态之间出现耦合趋势。

在悬臂板1/4弦向布置内埋件的情形，即工况ML ₂颤振图像与图9类似，得到的颤振速度为673.34 m/s，颤振频率为24.13 Hz，颤振发生在第1阶模态，依然是第2阶模态和第1阶模态耦合所致。

由此可以看出，当沿展向布置的多个内埋件逐渐向前缘移动时，悬臂板的颤振速度会有所提高，但却伴随着颤振频率的下降。期间，颤振模态会发生迁移，从第2阶扭转模态跳转至第1阶弯曲模态。

4 结论

基于假设模态法及一阶活塞理论得到带内埋质量超声速悬臂板在模态坐标下的动力学方程，引入p-k法在不同内埋工况下进行颤振计算，得到以下主要结论：

（1）内埋质量的存在会影响到悬臂板模态属性，并进而影响到悬臂板的颤振特性。随着内埋件质量、位置和数目的变化，悬臂板的颤振速度和颤振频率会在相当大的范围内发生变化，颤振模态也会发生跳转。

（2）在仅考虑单个内埋件时，悬臂板上存在两处较佳的挂载区域。一处是靠近翼根区域，颤振速度和颤振频率对内埋件质量不敏感；另一处是靠近翼梢区域的前缘位置，在此区域挂载可有效地提高悬臂板颤振速度。

（3）对于细长体，不同质量分配方案下的颤振速度和颤振频率曲线均具有类似的变化趋势，颤振速度的最大差异控制在7.0%左右。

（4）对于沿展向布置多个集中质量的情形，内埋件位置前移会导致悬臂板颤振速度的升高和颤振频率的下降，同时，颤振模态也会发生跳转。

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Chiba M， Sugimoto T.Vibration characteristics of a cantilever plate with attached spring-mass system［J］.Journal of Sound and Vibration，2003，260（2）：237-263.

2	赵永辉.气动弹性力学与控制［M］.北京：科学出版社，2007.

3	赵永辉，黄锐.高等气动弹性力学与控制［M］.北京：科学出版社，2015.

4	肖艳平，杨翊仁.复合材料机翼/外挂系统颤振特性分析［J］.应用力学学报，2017，34（3）：502-506，611.

5	陈晓明，冯志华，黄萌萌.附加集中质量悬臂板的有限元分析及实验验证［J］.机床与液压，2018，46（7）：14-17.

6	Aksencer T， Aydogdu M.Vibration of a rotating composite beam with an attached point mass［J］.Composite Structures，2018，190：1-9.

7	Rahmane A， Benmansour T， Bouakba M，et al.Factors influencing the effect of attached mass on dynamic behavior of laminate composite plates using Taguchi technique［J］.Journal of the Brazilian Society of Mechanical Sciences and Engineering，2018，40：66.

8	Pacheco D R Q， Marques F D， Ferreira A J M.Panel flutter suppression with nonlinear energy sinks： numerical modeling and analysis［J］.International Journal of Non-Linear Mechanics，2018，106：108-114.

9	Molina J E， Nunez P G F.Influence of mass matrix models on flutter computations［J］.Journal of Aerospace Engineering，2018，31（3）：04018020.

10	Bera K K， Chandiramani N K.Aeroelastic flutter control of a bridge using rotating mass dampers and winglets［J］.Journal of Vibration and Control，2020，26（23/24）：2185-2192.

11	Zhou J， Xu M L， Xia W.Passive suppression of panel flutter using a nonlinear energy sink［J］.International Journal of Aerospace Engineering，2020，2020：8896744.

12	Zhou J， Xu M L， Zha J，et al.The suppression of nonlinear panel flutter response at elevated temperatures using a nonlinear energy sink［J］.Meccanica，2021，56（1）：41-57.

13	Tian W， Zhao T， GU Y，et al.Supersonic flutter control and optimization of metamaterial plate［J］.Chinese Journal of Aeronautics，2021，34（11）：15-20.

14	Bahrami-Torabi H， Kerboua Y， Lakis A A.Finite element model to investigate the dynamic instability of rectangular plates subjected to supersonic airflow［J］.Journal of Fluids and Structures，2021，103：103267.

15	祁武超，张贺铭，田素梅.外挂物对大展弦比直机翼颤振特性的影响［J］.计算力学学报，2022，39（5）：598-607.

16	Qi W C， Wang M， Tian S M.Effects of mass attachments on flutter characteristics of thin-walled panels［J］.Aerospace，2022，9（12）：748-748.

17	Tian S M， Wang M， Qi W C.Effects of elastically supported boundaries on flutter characteristics of thin-walled panels［J］.Energies，2022，15（19）：7088.

18	Muñoz Á， GarcíaFogeda P.Active flutter suppre-ssion of a wing section in a compressible flow［J］.Aerospace，2022，9（12）：804.

19	Uymaz B.Vibration of CFFF functionally graded plates with an attached point mass at an arbitrary point in thermal environment［J］.Journal of Vibration Engineering & Technologies，2023，11（4）：1867-1888.

20	Kalosha J I， Zuyev A L.Asymptotic stabilization of a flexible beam with attached mass［J］.Ukrainian Mathematical Journal，2022，73（10）：1537-1550.

21	Dadoulis G I， Manolis G D.A note on analytical solutions for vibrations of beams with an attached large mass［J］.Archive of Applied Mechanics，2022，92（7）：1973-1982.

22	Mahmoud M A.Free vibrations of tapered and stepped，axially functionally graded beams with any number of attached masses［J］.Engineering Structures，2022，267：114696.

23	Simiriotis N， Palacios R.A numerical investigation on direct and data-driven flutter prediction me- thods［J］.Journal of Fluids and Structures，2023，117：103835.

Options

Outlines

模态框（Modal）标题

Abstract

Cite this article

1 带内埋质量悬臂板的颤振方程

图1 带内埋质量悬臂板的几何模型

2 颤振分析

3 数值算例

表1 悬臂板的物理参数

图2 颤振速度和颤振频率随模态截断数 r 的变化

图3 无内埋质量情形下的颤振计算结果

3.1 单个内埋集中质量的情形

图4 颤振计算结果（ mp = 0.05， x = b/2， y = a/2）

图5 不同挂载位置颤振计算结果

图6 内埋件在悬臂板面内的位置

图7 悬臂板颤振特性随内埋质量的变化（工况 L 1~L 3 ）

3.2 细长体的情形

表2 细长体质量分配方案 (g)

图8 不同质量分配方案下内埋细长体悬臂板的颤振特性

3.3 多个内埋集中质量的情形（展向布置）

图9 颤振计算结果

4 结论

References

**图4 颤振计算结果（ m_p = 0.05， x = b/2， y = a/2）**

图7 悬臂板颤振特性随内埋质量的变化（工况 L ₁~L ₃ ）