Construction of performance degradation indicators for rolling bearings based on PCA multi-model fusion

Liying JIANG; Hao GUO; He LI; Mingkun LIU; Leiming ZHANG

doi:10.3969/j.issn.2095-1248.2024.01.007

Journal of Shenyang Aerospace University >

2024 , Vol. 41 >Issue 1: 54 - 60

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.01.007

Information Science and Engineering

Construction of performance degradation indicators for rolling bearings based on PCA multi-model fusion

Liying JIANG ,
Hao GUO ,
He LI ,
Mingkun LIU ,
Leiming ZHANG

Expand

College of Automation，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2023-04-10

Online published: 2024-03-29

Fold

Abstract

The performance health indicator of rolling bearings constructed from a single model can only describes the performance degradation states of rolling bearings from a single perspective， which has certain limitations.To solve this problem， a method for constructing HI based on PCA multi-model fusion was proposed. The idea was to use SVDD， AAKR， and GMM models to construct the corresponding single model HI， and then fuse them through PCA. The first principal component was selected as SAG-HI， containing "multi angle" performance degradation information. Experimental results shows that compared to the HI of each single model， SAG-HI achieved 98.06% grey confidence level in maintaining reliability with rolling bearings， and its correlation， monotonicity， and robustness were the best. Envelope spectrum analysis verified its ability to accurately monitor early fault occurrences.

Key words： rolling bearings; support vector data; auto-associative kernel regression; gaussian mixture model; PCA; performance degradation indicators; multi-model fusion

Cite this article

Liying JIANG , Hao GUO , He LI , Mingkun LIU , Leiming ZHANG . Construction of performance degradation indicators for rolling bearings based on PCA multi-model fusion[J]. Journal of Shenyang Aerospace University, 2024 , 41(1) : 54 -60 . DOI: 10.3969/j.issn.2095-1248.2024.01.007

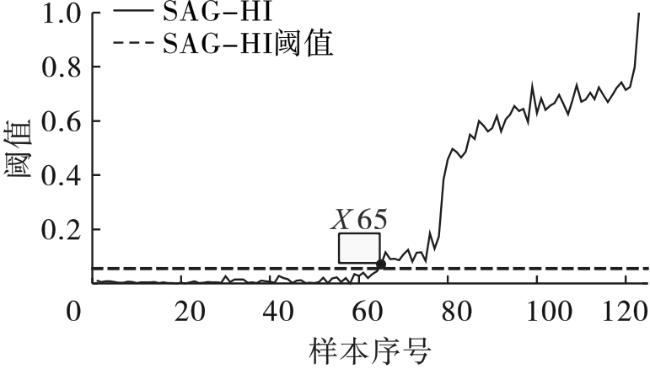
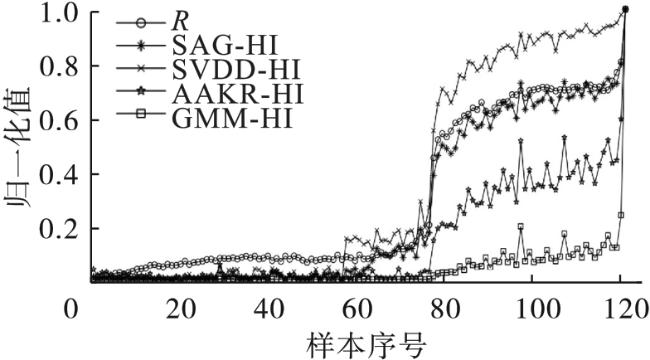
准确表征轴承运行中的性能退化程度，对保障系统的稳定运行至关重要。基于单模型的指标构建方法通过融合多种特征来共同描述轴承的性能退化状态。周建民等^［1］将无故障轴承振动信号的小波包奇异谱熵用来训练SVDD模型，并以此构建基于距离型的轴承性能退化指标。此指标在退化阶段描述退化趋势的能力较强，但SVDD模型对超球体外的特征向量表现过于敏感，易造成早期故障虚警的发生。Rai等^［2］通过集成经验模态分解（ensemble empirical mode decomposition，EEMD）提取了健康条件下轴承振动信号的固有模态分量的奇异值特征和能矩熵特征，以构建基准GMM，并输入全寿命样本的特征向量构成模型，将输出的后验概率的杰森-瑞丽散度（Jensen-Rényi，JRD）作为基于概率的性能退化指标，此退化指标在健康阶段稳定性较好，但在退化阶段描述退化趋势的能力较弱。刘路路^［3］用轴承健康样本的特征向量组成AAKR模型的健康记忆矩阵，并将全寿命样本的特征向量作为AAKR模型中的观察向量，以构建基于空间映射的性能退化指标。此指标虽基本能刻画出性能退化的趋势，但总体的鲁棒性较差。另外还可以用基于数据降维方法来构建多特征融合指标。Widodo等^［4］将滚动轴承的峰值、峭度和熵估计值，经PCA方法进行降维，并选取第一主成分作为轴承性能退化指标。

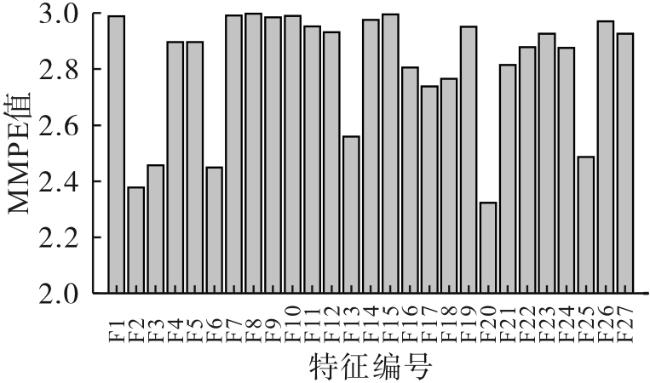
上述方法在构建健康指标前，没有考虑到特征之间会存在冗余性且未对各特征的重要程度作出评价。故本文利用类softmax函数^［5］对经过多尺度排列熵的均值（mean of multiscale permutation entropy，MMPE）阈值^［6］筛选后的特征赋予相应的权值。针对上述单模型健康指标在表征轴承全寿命区间内的性能退化状态时，均具有各自的优缺点。故基于优势互补的思想，本文提出了一种将基于距离型的单模型健康指标、基于空间映射的单模型健康指标和基于概率的单模型健康指标经PCA方法融合，并以分散程度最大的第一主成分分量构建多模型融合的健康指标。依据滚动轴承加速寿命实验数据集的实验结果，验证了本文所提方法的有效性和优越性。

1 理论基础

1.1 SVDD模型构建健康指标

SVDD基本思想是寻求一个最优超球体，使目标样本尽可能包含在球内，非目标样本尽可能排除在球外^［7］，该球体的半径和球心分别用

R

和

O

表示。用健康样本的特征向量

x h, h = 1, 2, ⋯, H

构建模型训练集。依据支持向量机理论，最优超球体的优化目标和需满足的约束条件为

m i n (R 2 + C ∑ h = 1 H ξ h) s . t . ‖ x h - O ‖ 2 ≤ R 2 + ξ h (ξ h ≥ 0, h = 1, 2, ⋯, H)

（1）

式中：

C

为惩罚参数；

ξ h

为松弛变量。

引入核函数

K (x j, x k)

（本文使用高斯核函数）可以解决在低维空间线性不可分的问题。超球体半径

R

为

R 2 = K (x s, x s) - 2 ∑ h = 1 H α h K (x h, x s) + ∑ j = 1 H ∑ k = 1 H α j α k K (x j, x k)

（2）

式中：

α

为拉格朗日乘子；

x s

为支持向量。任意一个全寿命样本中第

i

个样本的特征向量

x i

到超球体中心

O

的距离

D i

为

D i 2 = K (x i, x i) + ∑ j = 1 H ∑ k = 1 H α j α k K (x j, x k) - 2 ∑ h = 1 H α h K (x i, x h)

（3）

通过比较轴承的全寿命样本的特征向量

x i

到球心的距离

D i

与超球体的半径

R

之间的差值来描述轴承性能退化的状况。即由SVDD模型构建的健康指标为

H I S V D D (i) = 0, D i - R ≤ 0 D i - R, D i - R > 0

（4）

1.2 AAKR模型构建HI

AAKR模型构建

H I

^［8］的基本思想是将轴承健康状态下样本的特征向量构成健康记忆矩阵，将轴承全寿命样本的特征向量（观测向量）用健康记忆矩阵重构，可得到对应的重构估计向量，然后量化观测向量和其对应的重构估计向量之间的差异性，以构建表征轴承性能退化程度的指标。

对于含有

G

个特征参数的健康样本的特征向量所构建的健康记忆矩阵

E

为

E = x 1,1 x 1,2 ⋯ x 1, G x 2,1 x 2,2 ⋯ x 2, G ⋮ ⋮ ⋱ ⋮ x H, 1 x H, 2 ⋯ x H, G

（5）

式中：

x i, j

是第

i

个健康样本的特征向量中的第

j

个特征参数值。

对于任意观测向量

x i = x i, 1 x i, 2 ⋯ x i, G T

与记忆矩阵

E

中每个健康样本的特征向量间的欧式距离为

d z (E z, x i) = ∑ j = 1 G E z, j - x i, j 2 (z = 1,2, ⋯, H)

（6）

其在健康空间

E

的重构向量

x ˜ i

为

x ˜ i = ∑ z = 1 H w z E z ∑ z = 1 H w z

（7）

式中：

w z

为权重，计算公式为

w z = 1 2 π q 2 e - d z 2 2 q 2

（8）

式中：

q

是核函数的宽度系数。因此基于全寿命样本中的第

i

个观测向量x_i 与其对应的重构估计向量

x ˜ i

之间的欧氏距离所构建的健康指标为

H I A A K R (i) = x i - x ˜ i 2

（9）

式中：

• 2

表示两向量间欧氏距离运算。

1.3 GMM构建HI

GMM是一种将多个单高斯概率密度函数加权组合的参数模型，可描述数据样本在高维空间中的非椭球体分布。对于健康状态下样本的特征向量

x h, h = 1, 2, ⋯, H

，其GMM概率密度

p (x)

定义为

p (x) = ∑ j = 1 M b j l (x | μ j, σ j)

（10）

式中：

M

为高斯模型的数量；

b j

为各模型的混合权值，且

∑ j = 1 M b j = 1

；

μ j

为第

j

个高斯分布函数的均值向量；

σ j

为协方差矩阵；

l (x | μ j, σ j)

为单个高斯概率密度函数。

以最大化GMM的似然函数为目标，利用EM算法^［9］实现对GMM模型中的均值向量、混合权重和协方差矩阵的参数估计如式（11）所示。

J b j, μ j, σ j = ∑ h = 1 H l n (∑ j = 1 M b j (l (x j | μ j, σ j))

（11）

对于第

i

个全寿命样本的特征矢量

x i

，计算其GMM概率密度

P (x i)

，以表示

x i

属于由健康信号构成的GMM的概率大小，引入多域对数概率^［10］作为健康指标，其计算公式为

H I G M M (i) = l n (P (x i) + 10 - 22 l n (10 - 22)

（12）

2 基于PCA多模型融合的性能退化指标构建

2.1 多域特征提取

本文分别从时域、频域、时频域和熵的角度对轴承的振动加速度信号共提取27个原始特征来构建候选特征集，如表1所示。其中，时域特征^［11］可分为有量纲和无量纲特征共12个，频域特征共4个。由于相比于小波包分解系数，小波包节点能量比抗干扰的能力更强，故本文选用db10正交小波基，对滚动轴承振动信号进行三层小波包分解，将得到的8个子频带的能量比作为时频域特征^［12］，熵特征^［13］共3个。

表1 多域候选特征集

特征类型	特征名称及编号
时域特征	有量纲	均值F1、方根幅值F2、标准差F3、峰差F4、峰峰值F5、均方根值F6
时域特征	无量纲	偏度F7、峭度F8、峰值因子F9、振幅因子F10、波形因子F11、裕度因子F12
频域特征	平均频率F13、中心频率F14、频率均方根15、频率方差F16
时频域特征	8个子频带能量比F17~F24
熵特征	模糊熵F25、递归熵F26、样本熵F27

2.2 特征筛选和赋权

本文选用MMPE作为特征筛选的标准，MMPE即计算不同尺度下时间序列的排列熵的均值，其能够准确刻画出特征参数在多尺度上的复杂性与随机性，特别是对突变信息敏感性较强。同时为正确评价重要的特征成分，本文采用类softmax函数进行特征赋权，权值计算方法如式（13）所示。

W i = e 1 M M P E i ∑ j = 1 n e 1 M M P E j

（13）

式中：

W i

为第

i

个特征的权重；

M M P E i

为第

i

个特征的MMPE值。

2.3 多模型融合的性能退化指标构建方法与步骤

PCA以方差来衡量信息量的多少，在降低数据维度的同时最大程度保留了3种单模型健康指标中的有效信息，去除了3种单模型健康指标中具有较强相关性的冗余信息。PCA具有强化关键信息、计算开销较小和稳健性较强等优点，更加符合实际工程应用的需求。鉴于3种单模型的健康指标在全寿命区间内表征轴承性能退化状态时各自表现出的优势与不足之处，本文基于优势互补的思想，以3种单模型的健康指标为基础，采用PCA数据融合方法构建多模型融合的性能退化指标，该方法的主要步骤如下：

步骤1：收集轴承全寿命振动数据，确定样本长度

n

和样本数量

m

，原始数据样本记为

s i ∈ R n

，

i = 1, 2, ⋯, m

。

步骤2：多域特征筛选与赋权。假设从表1中共筛选出

g

种特征，并根据式（13）对这

g

种特征进行赋权，对原始数据样本

s i

提取这g种特征，组成的特征向量记为

x i ∈ R g

。

步骤3：构建单模型健康指标向量为

h i = H I S V D D (i) H I A A K R (i) H I G M M (i) T

（14）

步骤4：由m组样本构建矩阵 H

H = h 1 h 2 ⋯ h m T

（15）

步骤5：构建PCA模型。首先对 H 进行标准化处理，即计算样本均值向量

h ¯

和标准差向量

σ

，每个样本

h i

标准化处理后组成的矩阵记为

H ˜

，根据

H ˜

求出协方差矩阵 A，求出 A 特征值的最大值为

λ m a x

和其对应的特征向量

u m a x

，则变换矩阵

B = u m a x

。计算所有样本的主元得分向量

t

，如式（16）所示，找出

t

中的最大值

t m a x

和最小值

t m i n

。

t = H ˜ B

（16）

步骤6：对任意一个原始数据样本的特征向量

x i ∈ R g

，根据步骤3构建单模型健康指标向量

h i

，对其进行标准化处理，处理后的健康指标向量记为

h ˜ i

，则多模型融合的健康指标定义为

H I S A G (i) = h ˜ i T B - t m i n t m a x - t m i n

（17）

3 实验验证

3.1 实验数据描述

采用西安交通大学机械装备健康监测联合实验室的滚动轴承加速寿命测试平台试验数据对本文提出的方法进行验证，轴承加速寿命实验台如图1所示。实验轴承型号为LDKUER204。实验中设置采样频率为25.6 kHz，采样间隔为1min，每次采样时长为1.28 s。实验共设计了3类工况，每类工况下有5个轴承。本案例采用工况1的Bearing1_1数据，实际寿命123 min，最终失效位置为轴承外圈，共采集123组样本。本文每组样本选取2 000个代表数据。

显示原图|下载原图ZIP|生成PPT

图1 轴承加速寿命实验台

3.2 特征预处理和SAG-HI构建

计算得到27个特征的MMPE值如图2所示。选取筛选阈值MMPE=2.6，共筛选出6个优选特征，它们分别是方根幅值F2、标准差F3、均方根值F6、平均频率F13、第4个子频带能量比F20和模糊熵F25。并依据式（13）计算得到各优选特征的权值如表2所示。

显示原图|下载原图ZIP|生成PPT

图2 各特征对应的MMPE值

表2 优选特征对应的权值

特征

编号

F13

F20

F25

特征

权重

0.168 5

0.166 2

0.166 4

0.163 5

0.170 1

0.165 3

选取轴承全寿命样本中的前30组样本作为各模型健康训练样本集，设定各模型参数为：

q = 1

、

C = 0.3

和

M = 1

，构建

H I S A G

，经计算得到第一主成分的贡献率^［14］为95.45%。这说明第一主成分已几乎全部包含了3个单模型HI中全部的轴承性能退化信息。同时本文采用

3 σ

准则确定故障阈值，SAG-HI及其故障阈值如图3所示。

显示原图|下载原图ZIP|生成PPT

图3 SAG-HI及其故障阈值图

从图3可知，SAG-HI判定的初始退化时刻对应第65个样本。为验证其对初始退化点监测的准确性，分别对第64和第65个样本进行包络谱分析，结果分别如图4和图5所示。在图4中未发现与外圈故障特征频率

f = 107.9 H z

接近的频率成分。但在图5中可找到与

f

接近的频率成分

108.8 H z

，其幅值大小不太突出且包络谱中“地毯”噪声较大，可以确定轴承此时发生了早期外圈故障。这充分验证了SAG-HI能够准确地监测到早期故障的发生。

显示原图|下载原图ZIP|生成PPT

图4 第64个样本的包络谱图

显示原图|下载原图ZIP|生成PPT

图5 第65个样本的包络谱图

3.3 各模型健康指标对比与分析

为了定量评价各模型的健康指标在全寿命区间表征轴承性能退化状况的能力水平，将各模型的健康指标与轴承保持可靠性做灰关系评估^［15］。本文在置信水平为95%条件下，求得本征序列（健康样本序列）的最大熵估计区间为［-1.255，0.894］。以此可求得基于泊松过程的轴承保持可靠度序列

R

，

R

以及各模型的健康指标经归一化处理结果如图6所示。

显示原图|下载原图ZIP|生成PPT

图6 各模型的健康指标和保持可靠度序列 R 趋势

在灰关系权值系数

ω = 0.5

条件下^［16］，求得各模型的健康指标与保持可靠度序列

R

之间的灰置信水平，如表3所示。

表3 保持可靠度序列 R 与各模型健康指标的灰置信水平 (%)

各模型健康指标	SAG-HI	SVDD-HI	AAKR-HI	GMM-HI
灰置信水平	98.38	96.75	96.14	95.95

从图6可观察到保持可靠度序列

R

与SAG-HI的趋势走向最为贴近，且由表3可知，SAG-HI与保持可靠度序列R的灰置信水平最高。这充分表明了SAG-HI更符合实际的轴承性能退化演变规律。

采用相关性、单调性与鲁棒性指标来评价各模型健康指标在全寿命区间上的综合表现^［17］。计算得到各模型HI的相关性、趋势性与鲁棒性大小如表4所示。从表4可观察到SAG-HI的相关性（0.97）、单调性（0.42）以及鲁棒性（0.86）均表现为最优。证明了本文提出的多模型融合的性能退化指标构建方法的优越性。

表4 各模型健康指标的评价指标值

评价指标	相关性	单调性	鲁棒性
SAG-HI	0.97	0.42	0.86
SVDD-HI	0.94	0.31	0.74
AAKR-HI	0.71	0.25	0.71
GMM-HI	0.91	0.41	0.81

4 结论

本文所提出的SAG-HI可从距离、空间映射和概率3个角度共同表征轴承的性能退化状态。从上述实验可知，SAG-HI克服了单模型HI在表征性能退化指标时的本身局限性，更符合实际的轴承性能退化演变规律，同时能够及时准确地监测到早期故障的发生，这在工程实践中具有重要意义。

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	周建民，徐清瑶，张龙，等.结合小波包奇异谱熵和SVDD的滚动轴承性能退化评估［J］.机械科学与技术，2016，35（12）：1882-1887.

2	Rai A， Upadhyay S.An integrated approach to bearing prognostics based on EEMD-multi feature extraction，Gaussian mixture models and Jensen-Renyi divergence［J］. Applied Soft Computing Journal，2018，71（2）：36-50.

3	刘路路.基于特征融合和LSTM的滚动轴承剩余寿命预测［D］.成都：电子科技大学， 2021.

4	Widodo A， Yang B.Application of relevance vector machine and survival probability to machine degradation assessment［J］.Expert Systems with Application，2011，38（3）：2592-2599.

5	张康.基于全寿命信息与深度时序特征的滚动轴承健康指标构建方法研究［D］.上海：上海大学，2022.

6	董治麟.多尺度排列熵方法及其在滚动轴承智能故障诊断中的应用研究［D］.马鞍山：安徽工业大学，2020.

7	Alam S， Sonbhadra K S， Agarwal S，et al.Sample reduction using farthest boundary point estimation （FBPE） for support vector data description （SVDD）［J］.Pattern Recognition Letters，2020，131（3）：268-276.

8	田雯雯，吕丽霞，冯雪凯，等.基于改进AAKR的风电机组齿轮箱状态监测［J］.电子测量技术，2022，45（15）：158-165.

9	魏居辉，王炯琦，穆京京，等.基于高斯混合模型的卫星电源系统异常检测方法［J］.空间控制技术与应用，2022，48（4）：104-114.

10	张龙，黄文艺，熊国良，等.基于多域特征与高斯混合模型的滚动轴承性能退化评估［J］.中国机械工程，2014，25（22）：3066-3072.

11	Stack J R， Habetler T G， Harley R G.Fault-signature modeling and detection of inner-race bearing faults［J］.IEEE Transactions on Industry Applications，2006，42（1）：61-68.

12	孙建.滚动轴承振动故障特征提取与寿命预测研究［D］.大连：大连理工大学，2016.

13	Jin de Z， Tao L， Rui M，et al.Generalized composite multiscale permutation entropy and PCA based fault diagnosis of rolling bearings［J］.Journal of Vibration and Shock，2018，37（20）：61-66.

14	耿俊超，王天真，韩金刚，等.基于多级特征提取的并网逆变器故障诊断策略［J］.电源学报，2022，20（4）：28-36.

15	程立，马文锁，夏新涛，等.基于改进模糊熵和灰关系的滚动轴承性能退化评估［J］.机械传动，2022，46（1）：56-64，86.

16	叶亮，夏新涛，常振.滚动轴承振动性能的混沌特性与不确定性之间的灰关系评估［J］.机械传动，2021，45（1）：9-16，103.

17	常永祺. 机械旋转部件性能退化跟踪与剩余使用寿命预测方法研究［D］.哈尔滨：哈尔滨工业大学，2020.

Options

Outlines

模态框（Modal）标题

Abstract

Cite this article

1 理论基础

1.1 SVDD模型构建健康指标

1.2 AAKR模型构建HI

1.3 GMM构建HI

2 基于PCA多模型融合的性能退化指标构建

2.1 多域特征提取

表1 多域候选特征集

2.2 特征筛选和赋权

2.3 多模型融合的性能退化指标构建方法与步骤

3 实验验证

3.1 实验数据描述

图1 轴承加速寿命实验台

3.2 特征预处理和SAG-HI构建

图2 各特征对应的MMPE值

表2 优选特征对应的权值

图3 SAG-HI及其故障阈值图

图4 第64个样本的包络谱图

图5 第65个样本的包络谱图

3.3 各模型健康指标对比与分析

图6 各模型的健康指标和保持可靠度序列 R 趋势

表3 保持可靠度序列 R 与各模型健康指标的灰置信水平 (%)

表4 各模型健康指标的评价指标值

4 结论

References