在计算机科学和数据处理领域，高效的查找算法一直是学者们研究的重要问题之一。随着大数据时代的到来，数据量的急剧增加使得传统的查找方法面临着挑战。顺序查找［1］、二分查找［2-3］和哈希查找［4］等传统的查找算法在时间复杂度或空间复杂度上存在一定的局限性，无法满足快速、准确查找的需求。在数据分析统计问题上，对于给定的大量数据，如果要求快速统计出有多少对数据的运算结果在某个特定值或在某个特定范围内是非常困难的。例如在分析某一地区居民的贫富差距时，可以将收入差值在某一范围内的人口比例作为评价指标之一［5-6］，因此需要计算出收入差值在目标范围内的数对的数量，从而得到该差值的比率，最终进行建模分析。
在上述背景下，本文提出了一种基于双指针的线性搜索算法，用于解决统计差值对［7］的问题。统计差值对在许多实际应用中具有重要意义，例如在金融领域中用于分析股票价格波动的相关性，或者在生物信息学中用于识别蛋白质序列中的结构特征等。对于该问题，一般采用的算法是利用哈希表［8］存储所有数据，对每个数据进行枚举，统计出一共有多少对数据符合条件；或对所有数据排序后进行枚举，通过二分查找［9］的方法统计出结果。
数据量过大时，以上两种统计方法在时间或空间上均表现出不同的弊端。对此，本文设计了一种基于双指针的线性搜索算法，使用两个指针在数据集的同一侧出发，两个指针同时进行搜索，最终查找到目标数据。这种方法不仅比二分查找算法时间复杂度低，还解决了哈希查找算法对照哈希表查找时存储空间的浪费问题［10］，提高了解决此类问题的效率。
双指针在传统算法中也有较为广泛的应用，例如快速排序算法［11］、归并排序算法［12-13］等。本文将首先回顾现有的查找算法及其局限性，并阐述传统方法无法满足对于统计差值对问题的高效解决需求的原因。随后介绍双指针算法的基本原理和流程，详细说明其在解决统计差值对问题中的应用，并通过对算法复杂度的分析来比较双指针算法与传统方法的优势。最后，利用大量实验数据验证该算法的效率和准确性，并探讨其在实际应用中的推广。
该算法具有简洁高效的优点，不仅在统计差值对问题上表现出优异的性能，还具备广泛的应用前景。通过研究，希望能够提供一种高效、准确的解决方案，以满足在大数据处理和统计分析中的查找需求。
1 问题描述与算法设计
1.1 问题描述
本算法致力于解决统计差值对问题。统计差值对问题是在给定一组数据中，统计满足特定差值条件的数对数量。具体来说，给定一个包含n个整数的数组A以及一个目标差值d，需要计算出数组A中存在多少数对 ，满足 。
下面是一个具体的例子：
假设有以下数组 以及目标差值d=2，在数组A中找到满足 的数对数量。
首先，逐对比较数组中的数对，计算差值并检查是否等于目标差值d。
（2，5）->5-2=3≠2
（2，7）->7-2=5≠2
（2，10）->10-2=8≠2
（2，12）->12-2=10≠2
（5，7）->7-5=2=d，满足条件
（5，10）->10-5=5≠2
（5，12）->12-5=7≠2
（7，10）->10-7=3≠2
（7，12）->12-7=5≠2
（10，12）->12-10=2=d，满足条件
从上述比较中可以看出，数组A中存在两个数对的差值等于目标差值（d=2），即（5，7）和 （10，12）。因此，满足条件的数对数量为2。
在实际应用中，数组A可能包含成千上万个元素，而目标差值d可能是任意给定的值。
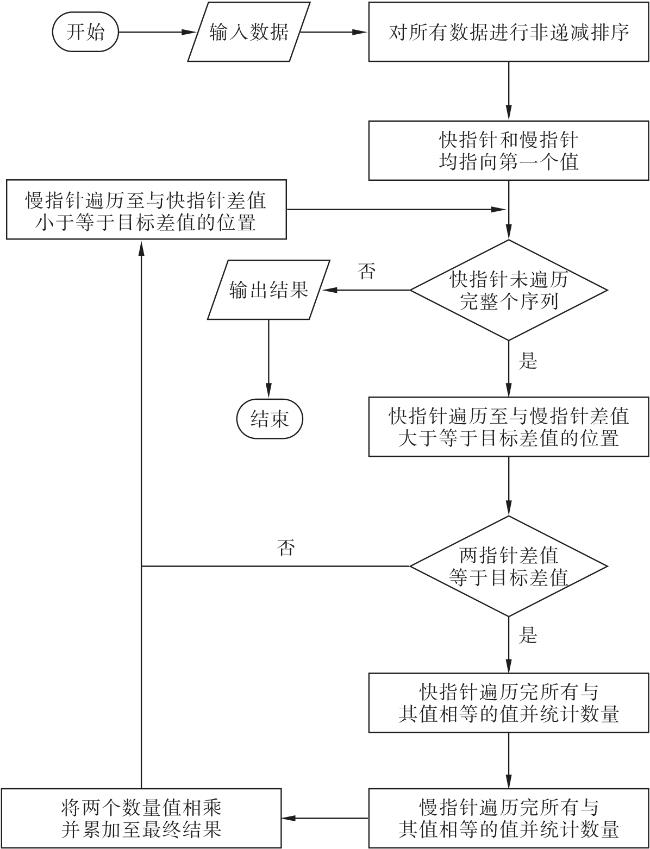
1.2 算法实现流程
对于统计差值对的需求，同向双指针线性搜索统计可以大幅度降低时间复杂度。在遍历对象的过程中，使用两个同向指针进行扫描，其中慢指针用于定位，快指针用于查找。双指针线性搜索算法充分利用数据有序这一特征，使同向快慢指针以不同的移动策略来完成搜索查找任务。
将差值对的差值设为c，x号元素均用a［x］来表示。如果结果与c值相等，那么快指针向后移动，直至遇到第一个与移动前元素不相等的值或移动到最后一个元素停止。接着慢指针向后移动，直至遇到第一个与移动前元素不相等的值时，分别记录两指针的移动次数。
如果结果小于c值，那么快指针向后移动，直至遇到第一个与移动前元素不相等的值或移动至最后一个元素停止；如果结果大于c值，那么慢指针向后移动，直至遇到第一个与移动前元素不相等的值。图1 为算法流程图。
对于c值等于0的特殊情况，即统计有多少对元素差值为0，只需定义一个指针，令该指针向后移动，直至遇到第一个与移动前元素不相等的值，在移动过程中记录指针移动次数。
差值对个数的计算公式为
式中：ans为记录符合题意的数对的个数； 是每一次移动的慢指针移动次数； 是每一次移动的快指针移动次数；cnt是差值为0时单指针移动次数。
双指针算法的优势在于它的时间复杂度通常为线性级别，即 ，其中n是数据结构的大小。这使得它成为处理大规模数据和需要高效查找问题的有效解决方案。同时，双指针算法不需要额外的存储空间，具有空间效率高的特点。
总而言之，双指针算法维护两个指针在数组中移动，根据特定条件来解决问题。在解决统计差值对问题中，通过移动指针的位置，可以快速有效地统计满足条件的数对数量。
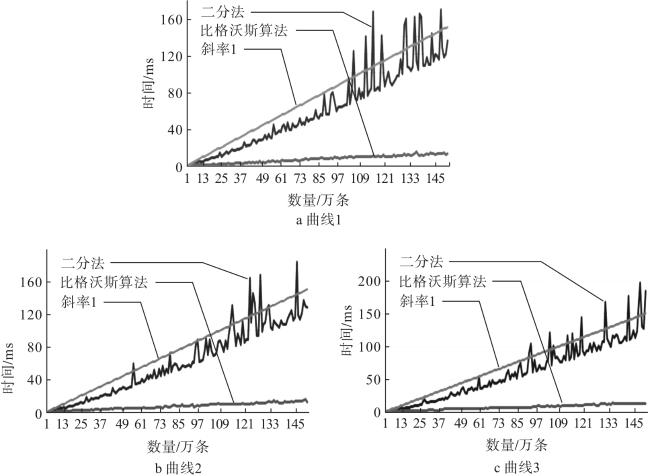
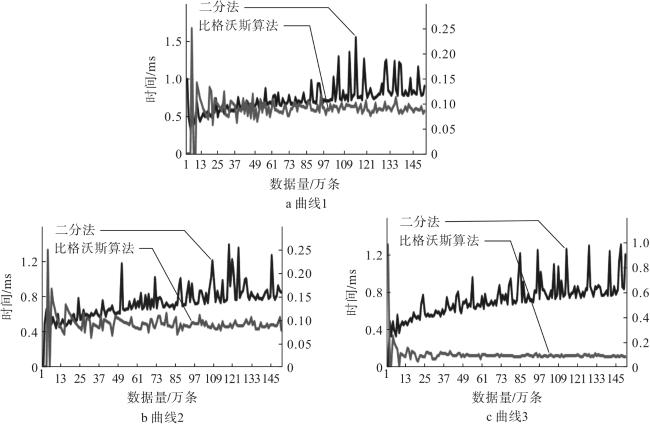
2 算法复杂度分析与对比
2.1 算法对比
表1 算法对比 |
| 算法名称 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 双指针算法 | ||
| 二分法 | ||
| 哈希 |
2.2 二分查找算法
对于二分查找算法，要求使用的数据结构必须是有序的。其通过将查找范围逐步缩小为一半来进行查找。首先，将查找范围的中间元素与目标值进行比较，如果相等，则查找成功；如果目标值小于中间元素，则在左半部分继续查找；如果目标值大于中间元素，则在右半部分继续查找。通过不断缩小查找范围，最终可以确定目标值是否存在。
二分查找的单次时间复杂度为 ，其中n是数字序列的长度。由于需要对每一个数字都进行一次二分查找算法，因此，利用二分查找解决差值对问题的总时间复杂度为 。
利用二分查找解决差值对问题的伪代码为
| 算法 二分查找算法BinarySearch（arr，target） |
|---|
| input： arr为排序好的所有数据target为目标值 output： 目标值target的数量 1 left<-0 2 right<-length（arr）-1 3 count<-0 4 while left<=right 5 do 6 mid<-（left+right）/2 7 if arr［mid］=target 8 do 9 count<-count+1 10 break 11 else if arr［mid］<target 12 do 13 left<-mid+1 14 else 15 do 16 right<-mid-1 17 end if 18 end while 19 return count |
2.3 哈希查找算法
哈希查找是通过哈希函数将待查找的键映射到一个存储桶（bucket）中。存储桶通常是一个数组或链表。当需要查找时，通过哈希函数计算键的哈希值，并在对应的存储桶中查找目标值。如果存在冲突（即多个键映射到同一个存储桶），则可以使用链表等方法解决冲突。
哈希查找的时间复杂度为 ，在遍历数字序列时，每次查找目标差值都是常数时间。而构建哈希表的时间复杂度为 ，其中n是数字序列的长度。因此，利用哈希查找解决差值对问题的总时间复杂度为 。空间复杂度取决于哈希表的大小，通常为 。
哈希查找算法解决差值对问题的伪代码为
| 算法 哈希查找算法Hash（A，n，C） |
|---|
| input： A为所有数据n为数据总量C为目标差值 output： 差值为C的对数 1 ans<-0 2 hashTable<-空的哈希表 3 for i from 0 to n-1 4 do 5 diff<-A［i］-C//计算目标差值 6 if hashTable.contains（diff） 7 do 8 ans<-ans+hashTable.get（diff）//将该差 值出现的次数累加到结果中 9 end if 10 if hashTable.contains（A［i］） 11 do 12 hashTable.set（A［i］，hashTable. get（A［i］）+1）//将当前元素的出现次数加1 13 else 14 hashTable.set（A［i］，1）//将当前元素的 出现次数设为1 15 end if 16 end for 17 return ans |
2.4 双指针算法时间复杂度
下面列出本文所描述的算法的时间复杂度与二分法进行对比的计算方法。
设n为每次查找数据的总量，T~D~表示二分法单次查找所需要的最大运算次数，可知
由于每次查找只需要查到当前位置之后的数据，因此查找量会逐渐降低。设问题数据总量为N，每次查找的数据量期望值为E（n），可知
根据参考文献［9］，二分查找的查找次数是均匀分布的，设期望次数为E（T~D~），由式（2） 和（3）可知
设二分法解决整个问题需要查找的次数期望值为E（S~D~），一共需要进行N次二分查找，则
由式（4） 和（5）可知
对于本文所描述算法，设其解决整个问题的次数期望值是 ，由于只需要遍历所有数据1次，因此
由式（6） 和（7）可知，两种算法的效率比R为
2.5 双指针算法空间复杂度
使用双指针算法解决差值对问题时，空间复杂度为O（1），即常数级别的额外空间。
双指针算法通常用于在一个数组或链表中进行遍历和搜索，而不需要额外的数据结构来存储中间结果。在差值对问题中，可以使用两个指针来维护一个子数组或区间，通过调整指针的位置来寻找满足条件的差值对。
具体而言，在差值对问题中，可以使用left和right两个指针同时从数组的两端开始移动。通过 的差值与目标差值C进行比较，根据比较结果来调整指针的位置，以逐步接近满足条件的差值对。
在双指针算法中，只需要两个额外的指针变量，因此不会随输入规模的增加而占用更多空间。无论输入数据的大小如何，空间复杂度始终保持为常数级别，即O（1）。这使得双指针算法在处理大规模数据时非常高效。
利用双指针算法解决差值对问题的伪代码为
| 算法 双指针算法Bigglesworth（A［］，n，C） |
|---|
| input： A为排序好的所有数据n为数据总量C为目标差值 output： 差值为C的对数 1 ans<-0，i<-0，j<-0 2 while i<n 3 do 4 while i<n and A［i］-A［j］<C 5 do 6 i<-i+1 7 end while 8 if A［i］-A［j］=c 9 do 10 cnt_i<-1，cnt_j<-1 11 while i<n and A［i<-i+1］=A［i-1］ 12 do 13 cnt_i<-cnt_i+1 14 end while 15 while j <n and A［j<-j+1］=A［j-1］ 16 do 17 cnt_j<-cnt_j+1 18 end while 19 ans<-cnt_i*cnt_j 20 end if 21 while j<n and A［i］-A［j］>C 22 do 23 j<-j+1 24 end while 25 end while 26 return ans |
3 实验结果分析
本节主要比较本文算法与二分查找的效率问题。算法效率一般比较时间复杂度和空间复杂度两个方面，本实验内容主要考虑时间复杂度，共进行3次实验，每次实验选取不同的C值。使用的操作系统为Windows10，硬件环境为AMD Ryzen 75 800 H with Radeon Graphics、内存8 GB、NVIDIA GeForce RTX3 070 Laptop、显存8 G，开发环境为Visual Studio 2019。
3.1 实验数据
数据生成方法：生成数据的过程基于预先设定的参数和随机数生成算法，以确保实验的可重现性。生成的数据集具有复杂的属性和多样性，可以模拟真实世界中的数据情况。
数据集规模和结构：生成的数据集包含150 000个观测样本，每个样本有10个属性（列）。每个属性为包含1到50位数字的字符串。数据集中的每个元素的值是根据随机数生成的，其中长度和正负号的选择是通过随机数来确定的。这样设计的目的是模拟真实数据中的复杂性，并提供一个具有挑战性的数据集。
为了评估数据的稳定性，进行了以下分析和讨论：
（1）随机数生成器：数据生成过程依赖于随机数生成器。对随机数生成器进行了严格测试，并验证了生成数据的随机性和一致性。
（2）实验重复性：为了评估数据的稳定性，多次运行了数据生成代码，并比较生成的多个数据集之间的差异。可以发现，在不同运行中生成的数据集在属性分布和整体结构上表现出一致性，这表明数据生成过程是可靠的。
（3）结果波动分析：对生成的数据集的属性进行统计分析，并比较不同运行中生成的数据集之间的结果差异。可以发现数据集之间存在一些随机波动，但总体趋势保持一致。这种波动可以理解为随机性带来的正常现象。
综合以上评估，认为生成的实验数据具有较高的稳定性。将使用这些数据来评估算法的性能，其中部分数据集如图2 所示。
3.2 实验结果
绘制本文算法和二分查找的时间复杂度曲线，并绘制与斜率为1的线性曲线对比图，如图3 所示。
由图3 可知，对于150万条数据，本文算法在15 ms内统计完成，二分查找算法需要140 ms左右，是本文算法时间的9倍。分析发现，与斜率为1的线性曲线对比，该算法的上升速率相对于二分查找算法非常小，基本呈缓慢性增长，总体波动也非常小。
在数据实验中，每轮在前一轮基础上加1万条数据进行实验，统计两种算法的每万条数据的平均处理时间，得到本文算法与二分算法的直接曲线对比，如图4 所示。
由图4 可以看出，在数据量逐渐增大的情况下，本文算法比二分查找算法的时间少，并且在数据量大的时候，处理平均速度趋于稳定。
从图3 和图4 可以看出，随着数据量的增大，基于双指针的线性搜索算法在处理时间上表现出较小的波动。无论是对比斜率为1的线性曲线还是每万条数据的平均处理时间，双指针算法都能维持较为稳定的高速处理效率，这意味着算法对于不同规模的数据集都能够保持相对一致的效率。
综上所述，基于双指针的线性搜索算法在处理时间上表现出较小的波动，并且在不同规模的数据集下都能够保持相对稳定的高效率。
3.3 对浮点数和负数的处理
双指针算法不仅在处理整数数据时表现出色，在处理包括浮点数和负数的数据集时同样具备优异性能。该算法采用了灵活的指针移动策略和差值计算公式，能够准确处理包括小数和负数在内的数据，保证结果的准确性和稳定性。
对于浮点数的处理，双指针算法在两个指针的移动过程中考虑到了数据的小数部分。通过合理地设置指针的步长，可以有效地遍历包括浮点数的数据集，并对其进行差值计算。这种处理方式使得算法能够适应多样化的数据类型，并且在处理精度要求较高的场景下表现出色。
在处理负数的情况下，双指针算法同样发挥着重要作用。通过合理设计算法的流程和判断条件，能够准确地识别负数之间的差值对，并进行统计。这种处理方式使得双指针算法在处理各种类型的数据时都具备更好的通用性和适应性，提高了算法的实用性和可靠性。
3.4 实际应用结果
将该算法实际应用在统计居民贫富差距上，使用数据集为2010-2019年中国部分城市与农村总收入，本文算法处理效果明显快于二分算法，并且在数据量可知情况下，本文算法的处理时间是可计算的。
双指针算法还可应用于学校成绩分析中，通过统计差值对的数量，可以识别学生们的学术差距，并据此制定针对性的教学策略。这对于提高教学质量和促进学生发展具有重要意义。
另一个应用领域是气温分析。通过统计气象数据中的差值对，可以研究温度变化趋势和异常情况。这种分析可以帮助气象部门更好地了解地区的气候状况，并及时采取相应的措施。
除此之外，双指针算法还可以应用于金融数据分析、图像处理等领域。在金融领域，可以利用双指针算法来进行股票交易模式的识别和分析，以便做出更准确的投资决策。而在图像处理方面，通过统计差值对可以实现图像质量评估和图像重建等任务。
这些实际应用展示了双指针算法在不同领域的灵活性和适应性，为进一步研究和应用提供了有价值的参考。
4 结论
通过多次实验结果分析，本文提出的基于双指针的差值对查找算法有着较低的时间复杂度，并且对内存的要求很低，在解决差值对统计问题中有着非常好的效果。与传统的遍历算法相比，双指针算法采用了两个指针分别定位于数据集的起始和结束位置，并根据特定的逻辑条件进行移动。这种双指针的迭代方式使得算法的时间复杂度降低，并且能够有效地遍历整个数据集以统计差值对的数量，尤其是在海量数据集上，这种优势更为显著，为高效数据分析提供了强有力的工具。双指针算法具备广泛的应用前景，并且可以为相关领域的数据分析问题提供高效、稳定的解决方案。