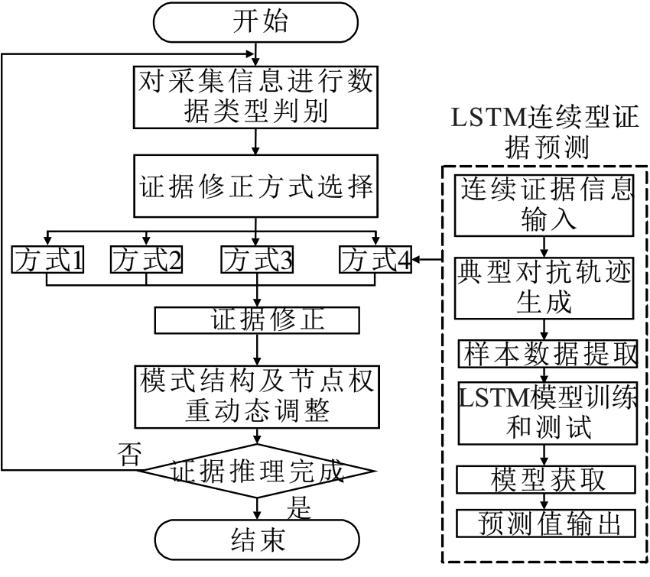
1 证据网络
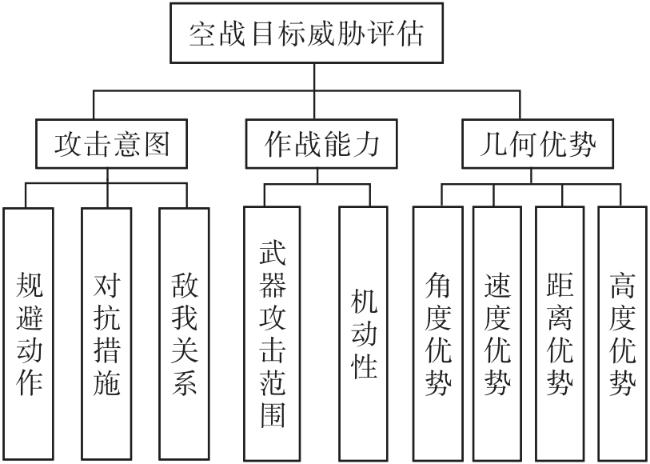
2 空战目标威胁评估指标体系构建
3 基于ECMDA-EN的空战目标威胁评估方法
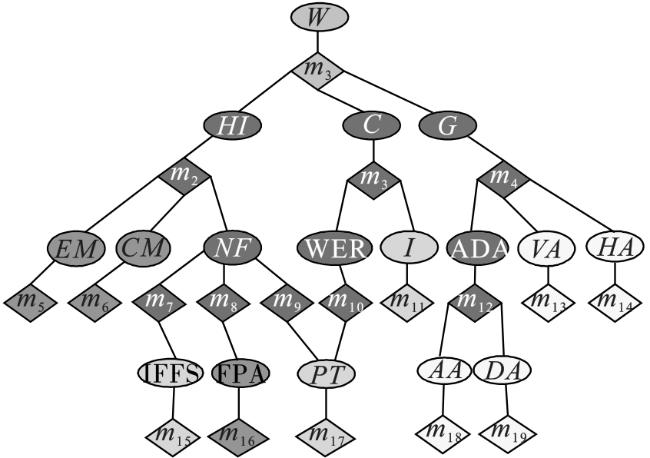
3.1 目标威胁评估模型
表1 模型变量说明 |
| 节点 | 含义 | 识别框架 | 说明 |
|---|---|---|---|
| W | 威胁等级 | {0,1,2} | 0-低;1-中;2-高 |
| HI | 攻击意图 | {0,1,2,3} | 0-最低;3-最高 |
| C | 作战能力 | {0,1,2} | 0-低;1-中;2-高 |
| G | 几何优势 | {0,1,2} | 0-低;1-中;2-高 |
| EM | 规避动作 | {0,1} | 0-错误;1-正确 |
| CM | 对抗措施 | {0,1} | 0-错误;1-正确 |
| NF | 敌我关系属性 | {0,1} | 0-友好;1-非友好 |
| WER | 武器攻击范围 | {0,1,2} | 0-小;1-中;2-大 |
| I | 机动性 | {0,1,2} | 0-低;1-中;2-高 |
| ADA | 角度、距离优势 | {0,1,2} | 0-低;1-中;2-高 |
| VA | 速度优势 | {0,1,2} | 0-低;1-中;2-高 |
| HA | 高度优势 | {0,1,2} | 0-低;1-中;2-高 |
| IFFS | 敌友识别 | {0,1} | 0-正确;1-错误 |
| FPA | 飞行计划协议 | {0,1} | 0-正确;1-错误 |
| PT | 平台类型 | {0,1,2} | 0-安全;1-中立;2-危险 |
| AA | 角度优势 | {0,1,2} | 0-低;1-中;2-高 |
| DA | 距离优势 | {0,1,2} | 0-低;1-中;2-高 |
表2 条件规则表 |
| 节点 | 条件 | 结果=[等级,信度] | 信任区间 |
|---|---|---|---|
| m 7 | IFFS=1 | NF=[0,1] | [0.95,1] |
| IFFS=0 | NF=[1,1] | [0.1,0.3] | |
| m 8 | FPA=1 | NF=[0,1] | [0.95,1] |
| FPA=0 | NF=[1,1] | [0.1,0.3] | |
| m 9 | PT=0 | NF=[0,1] | [0.5,1] |
| PT=1 | NF={[0,0.4][1,0.4] [{0,1},0.2]} | [0.5,1] | |
| PT=2 | NF=[1,1] | [0.5,1] | |
| m 10 | PT=0 | WER=[0,1] | [0.4,1] |
| PT=1 | WER={[1,0.4][2,0.4] [{1,2},0.2]} | [0.4,1] | |
| PT=2 | WER=[2,1] | [0.4,1] |
表3 加权融合规则表 |
| 节点 | 加权融合规则 |
|---|---|
| m 1 | T=HI+C+G |
| m 2 | HI=EM+CM+NF |
| m 3 | C=WER+I |
| m 4 | G=VA+HA+ADA |
| m 12 | ADA=AD∙DA |
3.2 证据修正模型的动态调整机制
3.2.1 4种证据修正方式
3.2.2 模型结构及节点权重的动态调整
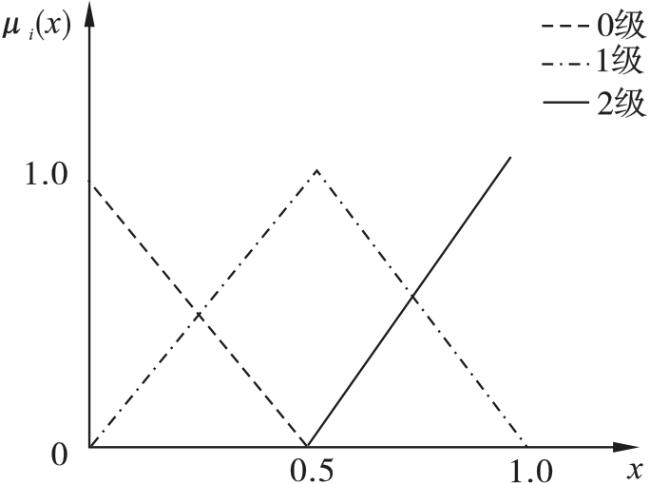
3.3 证据网络节点的信度结构转换
3.3.1 证据节点
3.3.2 中间节点
3.3.3 网络节点的信度结构转换
4 仿真算例
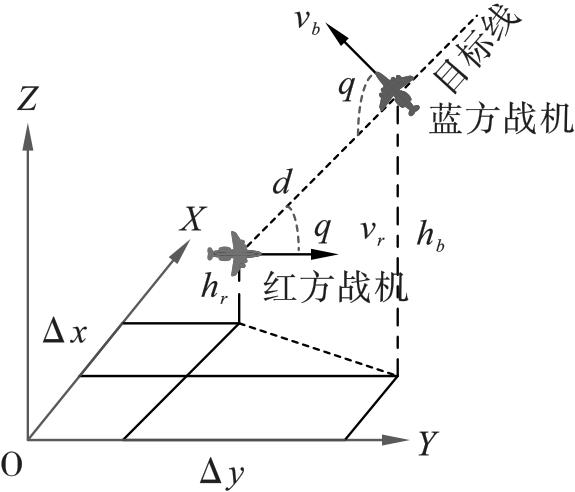
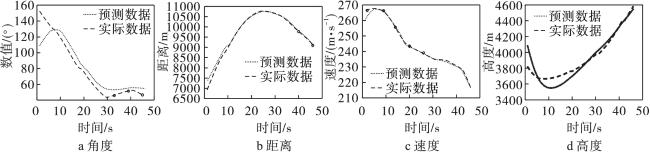
4.1 证据信息获取
表4 定量目标属性信息 |
| t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | |
|---|---|---|---|---|---|---|---|---|
| P/(°) | 139.96 | 138.49 | 149.89 | 151.73 | 134.70 | 118.79 | 96.27 | 87.45 |
| q/(°) | 148.63 | 130.33 | 105.21 | 80.09 | 55.70 | 46.01 --- | 49.64 --- | 49.37 260.33 |
| d/m | 7 178.62 | 8 693.22 | 9 769.61 | 10 479.28 | 10 770.97 | 10 577.66 | 103 68.17 --- | 9 597.63 2 053.62 |
| vr /(m·s-1) | 305.47 | 283.64 | 267.62 | 256.51 | 246.812 | 241.53 | 253.77 | 267.17 |
| vb /(m·s-1) | 269.56 1 166.47 | 269.72 --- | 259.99 --- | 247.83 --- | 243.25 690 | 235.18 | 232.13 | 213.04 |
| hr /(m·s-1) | 4 835.91 | 5 006.10 | 5 153.94 | 5 162.13 | 5 110.05 | 5 066.03 | 4 872.92 | 4 473.77 |
| hb /(m·s-1) | 3 896.2 | 3 765.92 | 3 695.80 | 3 760.87 | 3 876.19 | 4 001.07 | 4 231.49 | 4 595.79 |
表5 定性目标属性信息 |
| t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | |
|---|---|---|---|---|---|---|---|---|
| EM | 0.55 0.45 | 0.2 0.8 | 0.1 0.9 | 0.49 0.51 | 0.77 0.23 | 0.73 0.26 --- | 0.8 0.2 | 0.9 0.1 |
| CM | 0.8 0.2 | 0.1 0.9 | 0.33 0.67 --- | 0.85 0.15 | 0.74 0.26 | 0.8 0.2 | 0.8 0.2 | 0.9 0.1 |
| I | 0.25 0.65 0.1 | 0.2 0.59 0.2 --- | 0.1 0.35 0.55 | 0.3 0.65 0.05 | 0.25 0.7 0.05 | 0.3 0.65 0.05 | 0.65 0.3 0.05 | 0.65 0.3 0.05 |
| PT | 0.2 0.6 0.2 | 0.1 0.7 0.2 | 0.1 0.54 0.36 | 0.2 0.6 0.2 | 0.4 0.5 0.1 | 0.2 0.6 0.2 | 0.6 0.3 0.1 | 0.65 0.25 0.1 |
| FPA | 0.31 0.69 | 0.82 0.18 | 0.82 0.18 | 0.83 0.27 --- | 0.82 0.18 | 0.31 0.69 | 0.15 0.85 | 0.1 0.9 |
| IFFS | 0.42 0.58 | 0.51 0.49 | 0.59 0.41 | 0.61 0.39 0.13 0.87 | 0.55 0.45 | 0.42 0.58 | 0.21 0.79 | 0.1 0.9 |
4.2 证据修正
表6 目标证据修正结果 |
| t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | |
|---|---|---|---|---|---|---|---|---|
| AA/(°) | 0.15 0.85 0 | 0 0.98 0.02 | 0 0.79 0.21 | 0 0.64 0.36 | 0 0.60 0.40 | 0 0.62 0.38 | 0 0.75 0.25 | 0 0.80 0.2 |
| DA/(°) | 1.0 0 0 | 1.0 0 0 | 1.0 0 0 | 0 0 1.0 | 0 0 1.0 | 0 0 1.0 | 0 0 1.0 | 0 0 1.0 |
| VA/m | 0.24 0.76 0 | 0.1 0.9 0 | 0.07 0.93 0 | 0.06 0.94 0 | 0.01 0.99 0 | 0.02 0.98 0 | 0.18 0.82 0 | 0.46 0.54 0 |
| HA/(m·s-1) | 0.22 0.78 0 | 0.29 0.71 0 | 0.33 0.67 0 | 0.32 0.68 0 | 0.28 0.72 0 | 0.24 0.76 0 | 0.13 0.87 0 | 0 0.95 0.05 |
| EM | 0.55 0.45 | 0.2 0.8 | 0.1 0.9 | 0.49 0.51 | 0.77 0.23 | / | 0.8 0.2 | 0.9 0.1 |
| CM | 0.8 0.2 | 0.1 0.9 | / | 0.85 0.15 | 0.74 0.26 | 0.8 0.2 | 0.8 0.2 | 0.9 0.1 |
| I | 0.25 0.65 0.1 | 0.25 0.65 0.1 | 0.1 0.35 0.55 | 0.3 0.65 0.05 | 0.25 0.7 0.05 | 0.35 0.55 0.1 | 0.65 0.3 0.05 | 0.65 0.3 0.05 |
| PT | 0.2 0.6 0.2 | 0.1 0.7 0.2 | 0.1 0.54 0.36 | 0.2 0.6 0.2 | 0.4 0.5 0.1 | 0.2 0.6 0.2 | 0.6 0.3 0.1 | 0.65 0.25 0.1 |
| FPA | 0.31 0.69 | 0.77 0.13 | 0.82 0.18 | / | 0.82 0.18 | 0.31 0.69 | 0.15 0.85 | 0.1 0.9 |
| IFFS | 0.42 0.58 | 0.51 0.49 | 0.59 0.41 | 0.59 0.41 | 0.55 0.45 | 0.42 0.58 | 0.21 0.79 | 0.1 0.9 |
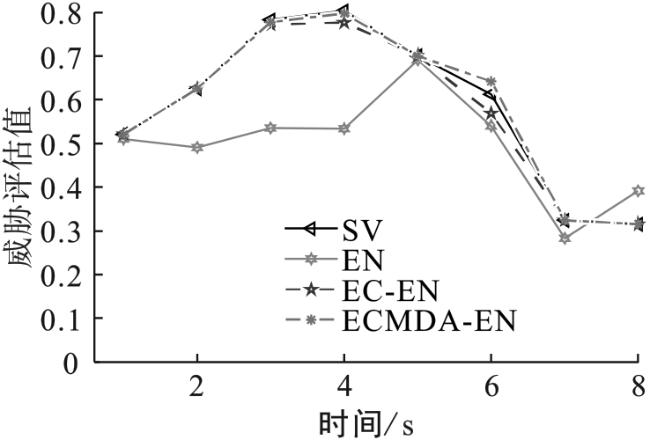
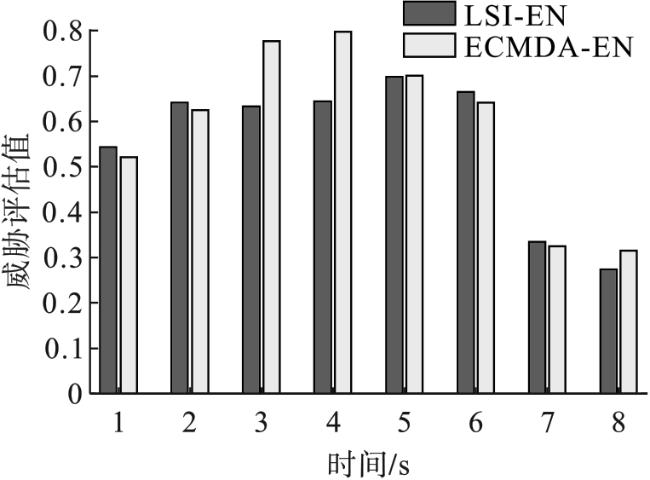
4.3 模型调整及ECMDA-EN推理
表7 变权节点规则调整 |
| 时刻 | 条件规则 |
|---|---|
| t3 | m1 :T=0.5HI+C+G |
| t4 | m 2:HI=EM+CM+0.5 |
| t6 | m 1:T=0.5+C+0.5G |
表8 目标威胁评估结果 |
| 等级 时刻 | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.059 6 | 0.017 9 | 0 | 0.004 1 | 0.016 5 | 0.054 1 | 0.351 8 | 0.369 3 |
| 1 | 0.839 1 | 0.713 4 | 0.4452 | 0.382 0 | 0.562 7 | 0.608 3 | 0.648 2 | 0.630 7 |
| 2 | 0.101 1 | 0.268 6 | 0.554 8 | 0.613 9 | 0.418 8 | 0.337 6 | 0 | 0 |