1 随机变分不等式的转化
2 随机变分不等式的二阶微分方程方法
3 数值实验
表1 总结了运用二阶微分方程系统(11)求解例1的数值结果。图1中给出了从所给的初始点出发,二阶微分方程系统(11)求解例1所得到的解的轨迹 。 |
| 时间/ms | x (t) | 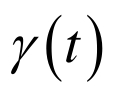 | 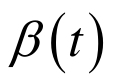 |
|---|---|---|---|
| 50 |  | 0.5 | 1 |
| 100 |  | 0.25 | 1 |
| 150 |  | 0.167 | 1 |


Journal of Shenyang Aerospace University >
Second-order differential equation method for solving stochastic variational inequality
Received date: 2023-03-31
Online published: 2023-11-09
A system of second-order differential equation with positive viscous damping coefficients and time-scale coefficients was applied to solve the stochastic variational inequality problem (SVIP). Firstly, the complementary function and the sample average approximation (SAA) method were applied to equate the original problem, and the stochastic variational inequality problem was transformed into a system of equations. Based on this, a second-order differential equation system with positive viscous damping coefficients and time-scale coefficients was established. Secondly, the convergence and convergence rate of the trajectory of the second-order differential equation system were obtained. Finally, two numerical experiments were presented to demonstrate the effectiveness of the second-order differential equation system in solving stochastic variational inequality problems.
Huiting ZHUANG , Li WANG , Juhe SUN , Danna JIA , Yanhong YUAN . Second-order differential equation method for solving stochastic variational inequality[J]. Journal of Shenyang Aerospace University, 2023 , 40(4) : 88 -96 . DOI: 10.3969/j.issn.2095-1248.2023.04.012
表1 总结了运用二阶微分方程系统(11)求解例1的数值结果。图1中给出了从所给的初始点出发,二阶微分方程系统(11)求解例1所得到的解的轨迹 。 |
| 时间/ms | x (t) | 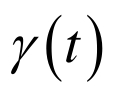 | 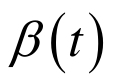 |
|---|---|---|---|
| 50 |  | 0.5 | 1 |
| 100 |  | 0.25 | 1 |
| 150 |  | 0.167 | 1 |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
杨振平.随机变分不等式问题及其在天然气市场中的应用研究[D].上海:上海大学,2019.
|
| 8 |
陈琦琼.不确定变分不等式及其在非合作博弈中的应用[D].南京:南京理工大学,2018.
|
| 9 |
|
| 10 |
R.Tyrrell Rockafellar and Roger J-B Wets.Stochastic variational inequalities:single-stage to multistage [J].Mathematical Programming,2017,165(1):331-360.
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
/
| 〈 |
|
〉 |