1 问题描述与假设
1.1 问题描述
1.2 问题假设
2 数学模型
2.1 目标函数
表1 集合、参数和变量定义 |
| 符号 | 定义 |
|---|---|
| 航班索引及所有航班集合 | |
| 机组人员索引及所有机组人员集合 | |
| 正机长,副驾驶索引 | |
| 两类机组人员的数量上限(具备机长资质、副驾驶资质) | |
| 匹配 中两类机组人员出现的个数 | |
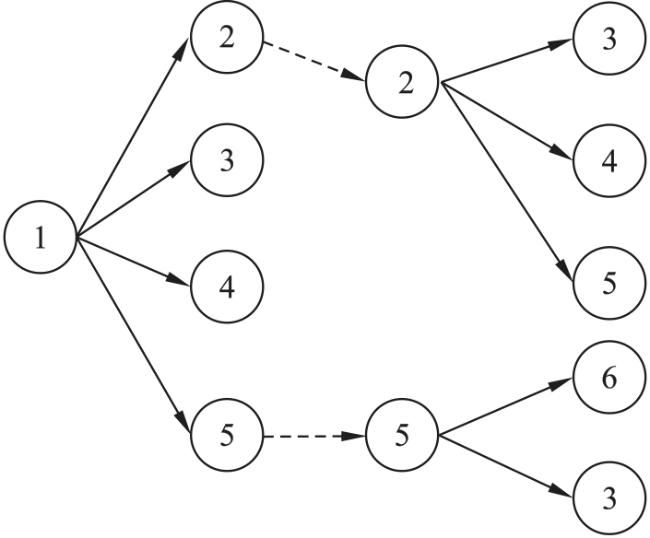
| 航班环,航班环集合 | |
| 一个可行航班环和一组机组人员构成的匹配索引及所有匹配的集合 | |
| 匹配 中所有航班 的集合 | |
| 0-1决策变量,若一个航班环 与机组人员构成的匹配 启用,则取1,否则取0 | |
| 0-1决策变量,若航班 因无法满足最低机组资质配置不能起飞,则取1,否则取0 | |
| 0-1参量,匹配 中的航班环内是否包含航班f,是则取1,否则取0 | |
| 0-1参量,匹配 中的航班 是否为置位航班,是则取1,否则取0 | |
| 航班 在航班环集 中出现次数 | |
| 航班f为置位航班情况下的置位人数 | |
| 前段到达及后段离港航班索引 | |
| ,s | 前段航班的终点及后段航班的起点 |
| 前段航班的到达时间及后段航班离港时间 | |
| 一条航班环中最早及最晚的航班 | |
| 一条航班环中最早及最晚的航班的终点 | |
| 最大飞行值勤小时数及飞行时间 | |
| 航班环 所包含的城市数 | |
| 航班环 所包含的航班数 |
2.2 约束条件
2.2.1 航班任务未完成的松弛约束
2.2.2 航班空间衔接约束
2.2.3 航班始发与终点空间约束
2.2.4 最小过站时间约束和最长过站时间约束
2.2.5 航班—机组人员对应唯一性约束
2.2.6 值勤时间约束
2.2.7 航班约束
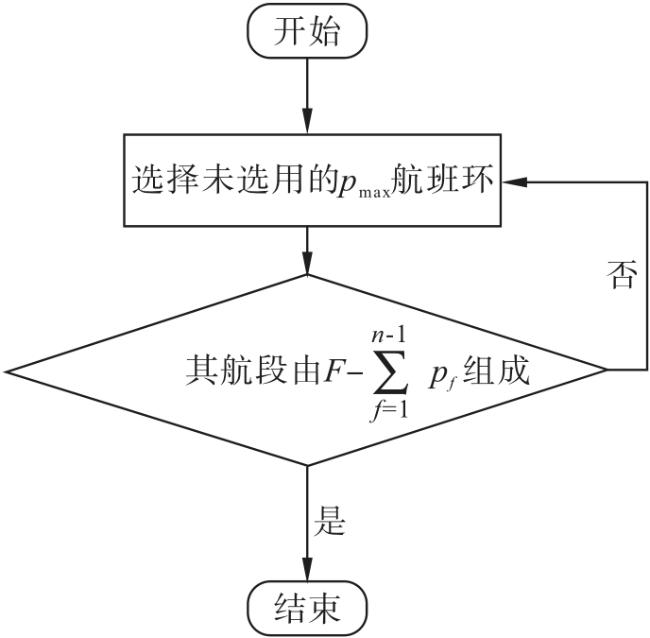
2.3 模型约简
3 算例分析
3.1 算例设置
表2 测试算例航班 |
| 序号 | 出发地 | 终点 | 出发时间 | 结束时间 |
|---|---|---|---|---|
| 1 | E | D | 12:05 | 14:35 |
| 2 | A | B | 6:25 | 7:55 |
| 3 | B | E | 7:15 | 9:30 |
| 4 | C | B | 13:45 | 15:55 |
| 5 | B | E | 7:00 | 8:05 |
| 6 | C | B | 15:45 | 17:25 |
| 7 | E | C | 11:00 | 12:45 |
| 8 | C | B | 13:45 | 15:35 |
| 9 | B | E | 8:45 | 10:05 |
| 10 | A | C | 10:30 | 12:45 |
| 11 | E | A | 16:30 | 17:50 |
| 12 | D | C | 11:30 | 14:25 |
| 13 | E | D | 14:35 | 16:55 |
| 14 | B | D | 6:45 | 8:15 |
| 15 | B | C | 6:25 | 8:35 |
| 16 | A | C | 10:35 | 13:15 |
| 17 | C | D | 13:25 | 14:55 |
| 18 | B | A | 8:15 | 9:35 |
| 19 | D | A | 16:00 | 18:00 |
| 20 | E | A | 12:00 | 15:30 |
| 21 | D | E | 13:50 | 14:55 |
| 22 | E | C | 12:40 | 14:35 |
| 23 | D | B | 18:05 | 19:25 |
| 24 | C | E | 10:45 | 12:20 |
| 25 | C | E | 10:35 | 13:35 |
| 26 | C | A | 15:35 | 17:20 |
| 27 | B | E | 8:35 | 10:25 |
| 28 | E | D | 10:30 | 13:25 |
| 29 | A | E | 12:50 | 14:25 |
| 30 | A | D | 9:35 | 12:55 |
| 31 | A | C | 10:00 | 12:05 |
| 32 | D | B | 14:20 | 17:15 |
| 33 | D | A | 15:30 | 16:55 |
| 34 | C | A | 16:25 | 17:35 |
| 35 | B | C | 6:35 | 9:25 |
| 36 | B | E | 9:00 | 11:05 |
| 37 | C | E | 14:35 | 15:40 |
| 38 | A | D | 8:25 | 10:15 |
| 39 | E | A | 15:55 | 17:35 |
| 40 | D | E | 9:25 | 11:35 |
| 41 | E | B | 15:15 | 16:35 |
| 42 | C | A | 9:30 | 11:55 |
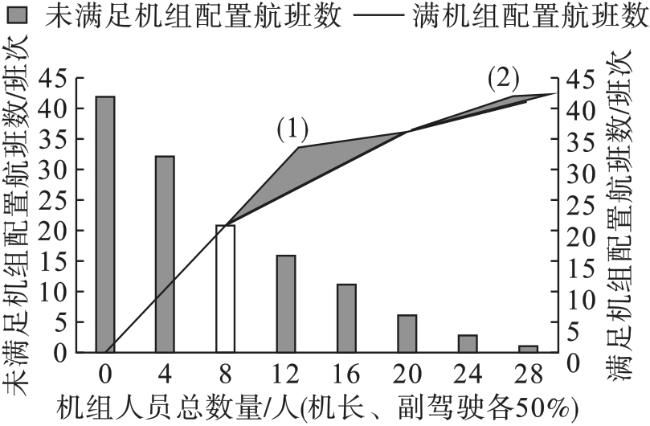
3.2 计算结果
表3 贪心算法机组排班结果 |
| 驻地A | 航班环 | 驻地B | 航班环 |
|---|---|---|---|
| 1 | 2-36-1-33 | 1 | 18-10-4 |
| 2 | 16-37-11 | 2 | 3-28-32 |
| 3 | 30-21-39 | 3 | 15-42-29-41 |
| 4 | 38-12-26 | 4 | 14-40-22-6 |
| 5 | 31-17-19 | 5 | 35-25-13-23 |
| 6 | 9-7-8 | ||
| 7 | 27-20 |
3.3 实验对比
表4 遗传算法机组排班结果 |
| 驻地A | 航班环 | 驻地B | 航班环 |
|---|---|---|---|
| 1 | 2-9-7-26 | 1 | 15-8 |
| 2 | 10-17-19 | 2 | 35-25-13-23 |
| 3 | 16-37-11 | 3 | 3-28-32 |
| 4 | 38-12-34 | 4 | 5-22-6 |
| 5 | 30-21-39 | 5 | 18-31-4 |
| 6 | 27-20 | ||
| 7 | 29-41 |
表5 两种算法计算结果对比 |
| 算法 | 计算时间/s | 未完成航班数 | 航班完成数 | 航班完成率/% | 置位 次数 |
|---|---|---|---|---|---|
| 贪心算法 | 24~26 | 3 | 39 | 93 | 1 |
| 遗传算法 | 24~28 | 7 | 35 | 83 | 1 |