1 先验知识和问题定义
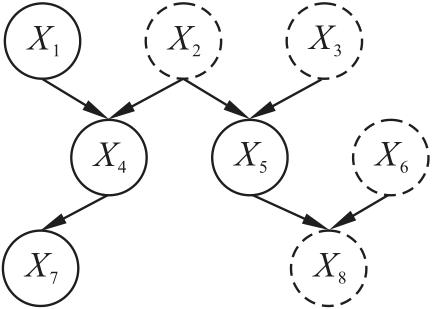
1.1 函数依赖
表1 部分美国医院信息表 |
| 变量 | Provider- Number | Hospital- Name | County- Name | Measure- Code | Measure- Name |
|---|---|---|---|---|---|
| t 1 | 10 001 | SAMC | houston | pn-5c | pxeumoxia |
| t 2 | 10 001 | SAMC | houston | pn-2 | heart attack |
| t 3 | 10 001 | SAMC | houston | pn-2 | pneumonia |
| t 4 | 10 005 | MMCS | marshall | ami-1 | heart attack |
| t 5 | 10 006 | ECMH | lauderdale | pn-2 | pneumonia |
| t 6 | 10 007 | MMH | covington | pn-2 | pneumonia |
| t 7 | 10 009 | HMC | morgan | pn-5c | pxeumoxia |
| t 8 | 10 018 | ACEFH | jefferson | scip-inf-6 | surgery |
| t 9 | 10 019 | HKMH | efferson | ami-1 | heart attack |
1.2 马尔科夫毯
证明:采用反证法,假设 不在 的马尔科夫毯中,根据函数依赖 可知, 值可以确定唯一的 值。假设 时,对应的 ,即 ,因此 。换言之,当给定 时, 一定为 ,与 中的属性取值无关,与马尔科夫毯条件独立性相违背,假设不成立,因此 一定在 的马尔科夫毯中。
1.3 问题定义
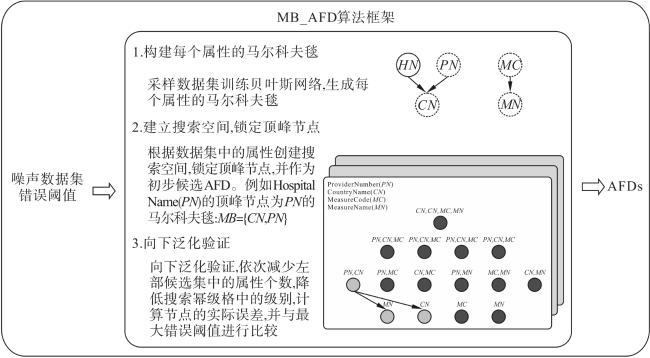
2 MB_AFD算法概述
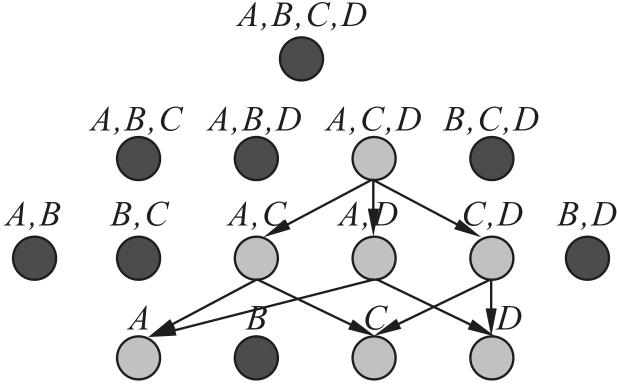
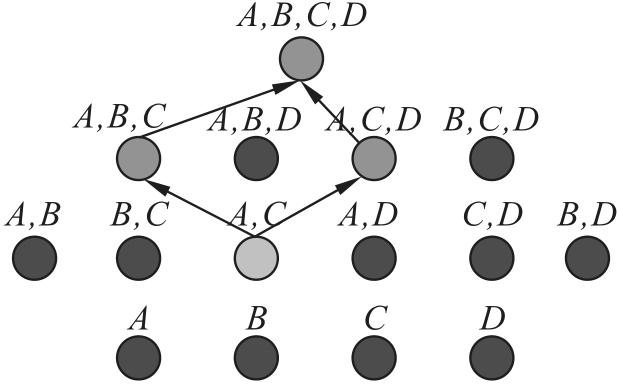
3 MB_AFD算法的搜索策略
3.1 构建每个属性的马尔科夫毯
3.2 向下泛化搜索算法
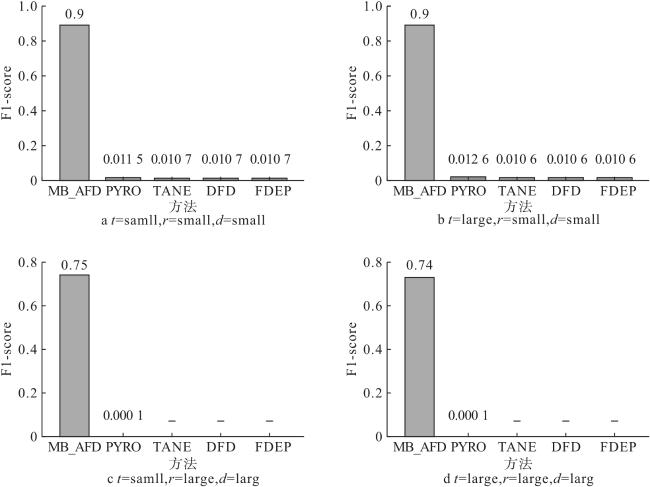
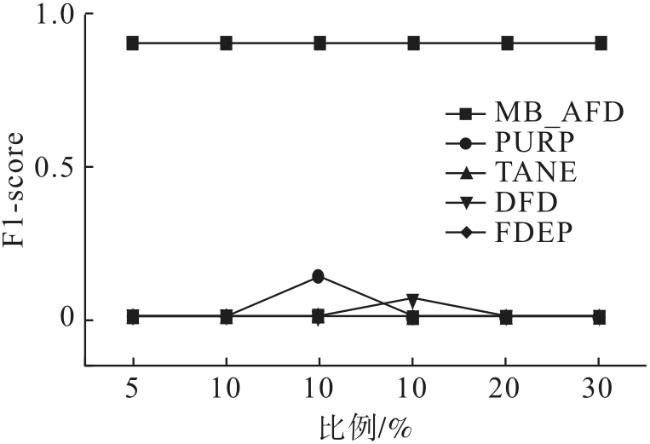
4 实验测试与结果分析
4.1 实验设置
表2 真实数据集基本信息 |
| 数据集 | 属性数量 | 元组数量 | 噪声率 |
|---|---|---|---|
| Rayyan | 11 | 1 000 | 0.086 |
| Beers | 11 | 2 410 | 0.159 |
| Flights | 7 | 2 376 | 0.298 |
| Hospital | 20 | 1 000 | 0.048 |
表3 合成数据集设置 |
| 参数 | 设置 |
|---|---|
| 元组数量t | 1 000(Small)100 000(Large) |
| 属性数量r | 8~16(Small)35~60(Large) |
| 域基数d | 64~180(Small)220~600(Large) |
4.2 真实数据实验对比分析
表4 真实数据集的对比实验结果 |
| 数据集 | 指标 | MB AFD | PYRO | TANE | DFD | FDEP |
|---|---|---|---|---|---|---|
| Rayyan | P R F1 | 0.429 1 0.6 | 0.027 1 0.053 | 0.026 1 0.051 | 0.026 1 0.051 | 0.026 1 0.051 |
| Beers | P R F1 | 0.23 1 0.374 | 0.022 1 0.043 | 0.022 1 0.043 | 0.022 1 0.043 | 0.022 1 0.043 |
| Flight | P R F1 | 0.2 1 0.33 | 0.09 1 0.165 | 0.09 1 0.165 | 0.09 1 0.165 | 0.08 1 0.148 |
| Hospital | R R F1 | 0.206 0.867 0.33 | 0.027 0.8 0.052 | 0.027 0.8 0.052 | 0.026 0.8 0.050 | 0.027 0.8 0.052 |