桌面式上肢康复机器人自适应柔顺性控制方法

叶长龙; 彭晶鑫; 于苏洋; 姜春英

doi:10.3969/j.issn.2095-1248.2024.05.007

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 5: 62 - 71

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.05.007

信息科学与工程

桌面式上肢康复机器人自适应柔顺性控制方法

叶长龙 ^,^a ,
彭晶鑫 ^b ,
于苏洋 ^b ,
姜春英 ^b

展开

^a. 沈阳航空航天大学，人工智能学院，沈阳 110136
^b. 沈阳航空航天大学，机电工程学院，沈阳 110136

叶长龙（1974-），男，辽宁锦州人，教授，博士，主要研究方向：机构学与机器人技术，E-mail：changlye@163.com。

收稿日期: 2024-04-25

网络出版日期: 2024-12-11

基金资助

辽宁省自然科学基金(20180520033)

收起

Adaptive compliance control method of desktop upper limb rehabilitation robot

Changlong YE ^,^a ,
Jingxin PENG ^b ,
Suyang YU ^b ,
Chunying JIANG ^b

Expand

^a. College of Artifical Intelligence, Shenyang Aerospace University，Shenyang 110136，China
^b. College of Mechatronics Engineering, Shenyang Aerospace University，Shenyang 110136，China

Received date: 2024-04-25

Online published: 2024-12-11

Fold

摘要

以一种六自由度桌面式上肢康复机器人（desktop upper limb rehabilitation robot，DULRR）为研究对象，观察到传统的位置控制无法满足患者康复训练的需求，可能导致其在康复过程中二次受伤。针对这一问题，提出一种基于位置闭环的自适应柔顺性控制方法。首先，根据DULRR的运动学模型，构建基于模糊比例-积分-微分（proportional-integral-derivative，PID）的位置控制器。然后，利用阻抗模型将力信号转换为速度和位置信号的特点，提出了基于压力传感器的自适应柔顺性控制器，与所提出的模糊PID控制器相结合，形成了完整的DULRR被动康复训练控制方法。最后，通过仿真分析和样机实验的方式，验证了基于位置闭环的自适应柔顺性控制方法的优越性。实验结果表明：相较于传统的PID控制器，在DULRR系统下模糊PID响应时间更短、稳态误差更小，体现出了较好的轨迹跟踪能力。同时，该控制器表现出良好的柔顺性效果，满足了患者早期被动康复训练的需求，并避免了康复过程中的二次伤害。

关键词： 康复机器人; 全方位移动机器人; 运动学模型; 模糊PID; 自适应柔顺控制

本文引用格式

叶长龙 , 彭晶鑫 , 于苏洋 , 姜春英 . 桌面式上肢康复机器人自适应柔顺性控制方法[J]. 沈阳航空航天大学学报, 2024 , 41(5) : 62 -71 . DOI: 10.3969/j.issn.2095-1248.2024.05.007

Abstract

Taking a six degrees of freedom desktop upper limb rehabilitation robot （DULRR） as the research object，it was observed that traditional position control cannot meet the needs of patient rehabilitation training and may lead to secondary injuries during the rehabilitation process.To address this issue，a position closed-loop adaptive compliance control method was proposed.Firstly，based on the kinematic model of DULRR，a position controller based on fuzzy PID was constructed.Then，utilizing the impedance model’s ability to convert force signals into velocity and position signals，an adaptive compliance controller based on pressure sensors was proposed.Combined with the proposed fuzzy PID controller，a complete DULRR passive rehabilitation training control method was formed.Finally，the superiority of the adaptive compliance control method based on position closed-loop was verified through simulation analysis and prototype experiments.The experimental results show that compared with traditional PID controllers，fuzzy PID in the DULRR system has shorter response time and smaller steady-state error，demonstrating better trajectory tracking ability.Meanwhile，the controller exhibits good flexibility，meeting the needs of early passive rehabilitation training for patients and avoiding secondary injuries during the rehabilitation process.

Key words： rehabilitation robot; omni-directional mobile robot; kinematic model; fuzzy PID; adaptive compliant control

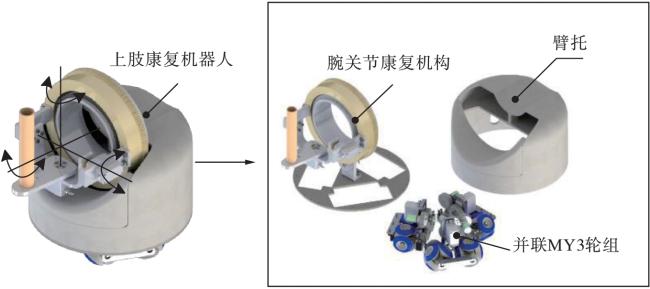
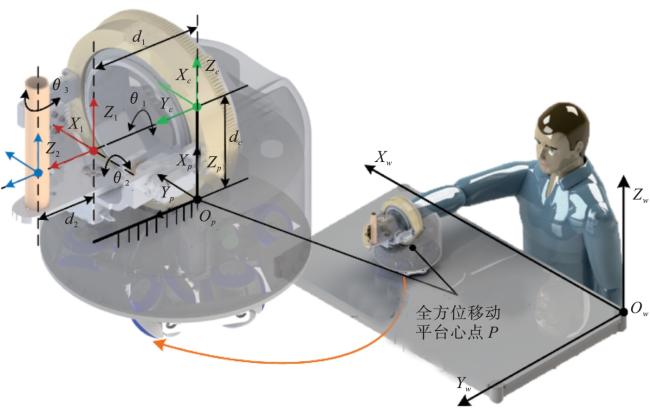
近年来，随着人们生活方式的改变和人口老龄化，脑卒中患者数量显著增加，全球脑卒中患者超过8 000万^［1］。脑卒中通常会导致人类的肢体功能障碍，例如偏瘫和截瘫。目前，瘫痪患者的康复治疗包括物理治疗、康复训练等^［2］。康复训练是康复医学中采用职业治疗和物理治疗相结合的中枢神经系统损伤偏瘫患者的治疗方法^［3］。有别于传统的康复训练，在康复训练中融入机器人技术，可以有效节省人工成本和治疗费用，提高康复训练效果。因此，康复训练机器人成为研究热点^［4］。针对不同的患肢，康复机器人可分为上肢康复机器人和下肢康复机器人。本文主要提出一种适用于DULLR的基于位置闭环的柔顺性控制方法。

1986年Maples等^［5］提出了阻抗控制的概念，发现将力反馈信号转换为位移误差和速度误差可以实现刚度和阻尼控制，通过刚度和阻尼控制相结合来实现阻抗控制。一系列阻抗控制方法被应用于康复机器人研究当中，例如，Santos等^［6］介绍了一种模块化下肢外骨骼机器人的最优阻抗控制器。Huo等^［7］介绍了一种使用测角仪、肌电图和力敏电阻（force sensing resistor，FSR）传感器的膝关节人外骨骼机器人阻抗降低控制器。Sado等^［8］在上肢康复机器人中使用一个简单的阻抗控制器，具有恒定的刚度和阻尼比，可以由医师调整^［9］。上述所有控制器各有优缺点，由于环境的不确定性，如粗糙的平面和桌面上的干扰物及一些额外干扰，使恒定刚度和阻尼柔顺性控制不能很好地适应环境的变化^［10］。自适应阻抗控制能很好地解决这一问题。例如，Roveda 等^［11］通过模型预测最优控制的方法预测了阻抗控制中的刚度和阻尼，从而达到变阻抗效果，以满足机器人在不同环境中的应用。Mujica等^［12］开发了一种鲁棒变导纳控制器以满足人机合作过程中对未知载荷的适应性。Zhong等^［13］开发了一种基于非线性扰动观测器的自适应双边阻抗控制器在人机交互过程中使用户更舒适。Foroutannia 等^［14］提出了一种自适应模糊阻抗控制器，该控制器主要管理人、机器人和环境之间的机械相互作用，并处理内部控制参数的不确定性。

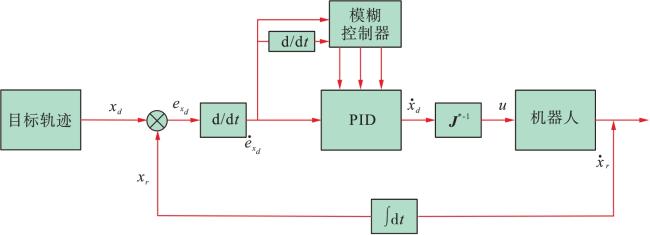
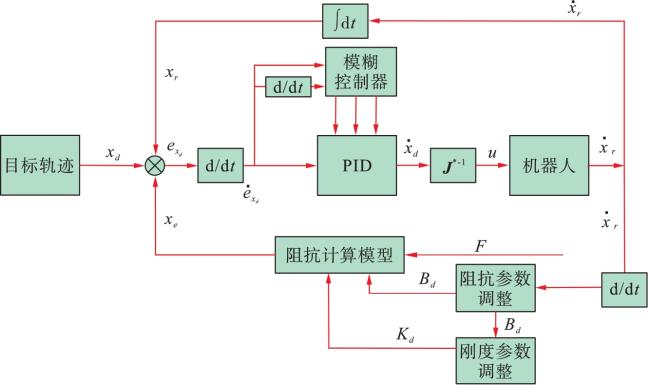
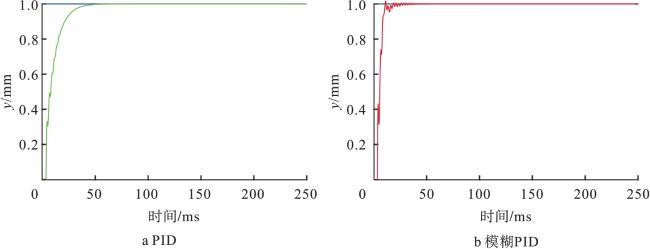
对于DULLR，自适应柔顺性控制是一个很好的方法，能够根据环境的变化自适应产生柔顺效果。本文方法分以下两个步骤实现：首先，采用模糊PID控制器，对轨迹进行良好跟踪。然后，采用基于位置的自适应柔顺性控制器，在改变运动速度和方向的情况下保持稳定性。该控制器可根据患者的特征和训练环境在物理治疗运动中获得较好的柔顺效果。因为阻抗系数是可变的，根据末端力传感器数据会每次迭代阻抗控制参数系数。

1 上肢康复机器人系统分析

1.1 机器人结构简介

桌面式上肢康复机器人机械结构如图1所示，它由全方位移动平台（MY3OMR）、一个腕关节康复机构和臂托组成。MY3OMR由3个MY3模块和3个电机组成。3个MY3模块以120°的间隔安装，每个模块由2个MY3轮组成，以45°错位平行排列。MY3轮采用外差速器、传动轴与平行轮一体的结构设计。腕关节康复机构由3个腕部扭转康复训练单元（旋前/旋后）、腕部俯仰摆转康复训练单元（桡屈/尺屈）及腕部水平摆转康复训练单元（背伸/掌屈）组成，且3个单元均采用电机直联的形式，提高传动效率和康复运动的精确度。详细结构介绍和硬件组成系统见文献［15］。

显示原图|下载原图ZIP|生成PPT

图1 桌面式上肢康复机器人机械结构图

1.2 上肢康复机器人的运动学模型

根据文献［15］，DULLR的坐标系定义如图2所示。其中：

d c

为从全向移动平台的中心点到基本坐标系的距离；

d 1

为从基本坐标系到手腕坐标系的距离；

d 2

为手腕坐标系到末端坐标系的距离；

θ 1

为腕关节回转的转角；

θ 2

为腕关节垂直摆动角度；

θ 3

为腕关节水平摆动角度。DULLR的末端姿态相对于桌面坐标系的齐次矩阵变换可以被描述为

显示原图|下载原图ZIP|生成PPT

图2 DULLR坐标系定义图

T = T 1 T 0 = R w P w 01 = n x 1 o x 1 α x 1 p x 1 n y 1 o y 1 α y 1 p y 1 n z 1 o z 1 α z 1 p z 1 0001 1

式中

R w = c p n x - s p n y c p o x - s p o y c p α x - s p α y s p n x + c p n y s p o x + c p o y s p α x + c p α y n z o z α z

；

P w = c p p x - s p p y + x p s p p x + c p p y + y p d c + p z

；

ω p = x p y p θ p T

为全方位移动平台的位姿。

其中，各参数为

n x = - s 1 s 2 c 3 + c 1 s 3; n y = - c 2 c 3; n z = - c 1 s 2 c 3 - s 1 s 3;

o x = s 1 s 2 s 3 + c 1 c 3; o y = c 2 s 3; o z = c 1 s 2 s 3 - s 1 c 3;

a x = s 1 c 2; a y = - s 2; a z = c 1 c 2;

p x = (- s 3 s 2 c 3 + c 1 s 3) + s 1 c 2 d 2;

p y = - c 2 c 3 - s 2 d 2 + d 1;

p z = - (c 1 s 2 c 3 + s 1 s 3) + c 1 c 2 d 2;

c i = c o s θ i; s i = s i n θ i

分别分析DULLR的整体线速度和角速度，得到DULLR的雅可比速度。所以DULLR的线速度方程可由式（1）中的元素

P w

得到。

P ˙ w . = J v * φ ˙ i θ ˙ i 6 × 1 T

（2）

J v * = M 0 00 3 × 6 + J θ p, θ i 3 × 4 N 0 0 I 4 × 6

（3）

其中：

M = - 2 s i n θ p - 2 s i n (π 3 - θ p) 2 s i n (π 3 + θ p) - 2 s i n θ p - 2 c o s (π 3 - θ p) 2 c o s (π 3 + θ p)

；

N = r 3 L r 3 L r 3 L

；

J θ p, θ i 3 × 4

为腕关节康复机构雅可比矩阵，可直接得到。

可实现上肢康复机器人的角速度方程如下。

R ˙ w . = J ω * φ ˙ i θ ˙ i 6 × 1 T

（4）

J ω * = 0,0, R p w z 0, ⋯, R 3 w z 0 3 × 6 00 N 0 0 I 6 × 6 5

式中：

z 0 = 001 T

；

R 1 w = R p w R o t Y c, θ 1

；

R 2 w = R p w R o t Y c, θ 1 R o t X 1, θ 2

；

R 3 w = R w

；

因此，上肢康复机器人雅可比矩阵为

J * = J v * J w * T

（6）

2 基于位置闭环的自适应柔顺性控制器设计

2.1 基于模糊PID的位置控制器设计

桌面式上肢康复机器人的模糊PID的位置控制框图如图 3 所示。整个系统的输入量为机器人系统的目标轨迹

x d

。整个系统的偏差

e x d

经过微分计算可以得到

e ˙ x d

，

e ˙ x d

再经过模糊PID控制器获得被控对象的目标速度

x ˙ d

，被控对象的目标速度

x ˙ d

经过DULLR的速度雅可比可计算矩阵计算得到每个电机的转速

u

。被控对象完成运动通过编码器返回机器人速度

x ˙ r

，

x ˙ r

再经过积分计算得到位置信息

x r

。

显示原图|下载原图ZIP|生成PPT

图3 基于模糊PID的位置控制框图

传统的PID控制系统依靠K_p、K_i、K_d 3个参数的协调作用来实现机器人的轨迹跟踪^［16］。但是，只使用一组参数进行控制，无法考虑机器人自身的特性和外界的干扰。机器人的运动精度和稳定性将受到很大影响。为了解决传统PID控制系统存在的问题，本文将模糊控制理论应用到PID控制系统中，并通过仿真实验验证了控制系统的优越性。模糊自适应PID控制^［17］可以根据控制对象反馈的参数误差e和变化率ec，找出PID控制系统参数K_p、K_i、K_d 与参数误差和变化率之间的模糊关系。

根据Cao等^［18］的经验和DULLR实际情况，输入时选择高斯型隶属度函数，输出时选择三角形隶属度函数。为方便计算，一般将输入和输出的模糊论域归一化，即e、ec的论域为

- 1,1

，K_p、K_i、K_d 的输出论域为

- 1,1

。进一步，通过论域进行模糊划分来确定模糊子集，模糊子集的作用是用来描述模糊计算过程中的不确定性和模糊性。一般情况下，模糊子集为3~9个，本文的上肢康复机器人系统为模糊控制器选择了7个模糊子集，分别为：负大（NB）、负中（NM）、负小（NS）、零（Z）、正小（PS）、正中（PM）、正大（PB），让其在保证控制精度的同时具有高效的运算能力。

模糊规则一般通过专业人员的经验获得。本文模糊规则推理采用Mamdani类型^［18］。受控过程中K_p、K_i、K_d 参数在不同e、ec条件下的自整定要求可简单概括为：（1）若系统输出大于理想输出，减小K_p；（2）如果系统响应时间大于要求的响应时间，则增大K_i，如果调整K_i 不能减少响应时间，则适当调整K_p；（3）若系统稳态输出波动，适当增大K_d；（4）如果系统干扰信号下的输出波动较大，适当减小K_d。根据上述规则，列出PID控制系统参数自整定的3个参数K_p、K_i、K_d 的模糊控制规则表，如表1—3所示。

表1 K_p 的模糊控制规则

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PB	PM	PM	PS	ZO	ZO
NM	PB	PB	PM	PS	PS	ZO	NS
NS	PM	PM	PM	PS	ZO	NS	NS
ZO	PM	PM	PS	ZO	NS	NM	NM
PS	PS	PS	ZO	NS	NS	NM	NM
PM	PS	ZO	NS	NM	NM	NM	NB
PB	ZO	ZO	NM	NM	NM	NB	NB

表2 K_i 的模糊控制规则

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NM	NM	NM	ZO	ZO
NM	NB	NM	NM	NM	NS	ZO	PS
NS	NM	NM	NS	NS	ZO	PS	PS
ZO	NM	NM	NS	ZO	PS	PM	PM
PS	NS	NS	ZO	PS	PM	PM	PM
PM	NS	ZO	PS	PS	PM	PB	PB
PB	ZO	ZO	PS	PM	PM	PB	PB

表3 K_d 的模糊控制规则

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PS	NS	NB	NB	NB	NM	PS
NM	PS	NS	NB	NM	NM	NS	ZO
NS	ZO	NS	NM	NM	NS	NS	ZO
ZO	ZO	NS	NS	NS	NS	NS	ZO
PS	ZO	ZO	ZO	ZO	ZO	ZO	ZO
PM	PB	NS	PS	PS	PS	PS	PB
PB	PB	PM	PM	PM	PS	PS	PB

2.2 自适应柔顺性控制器设计

在被动康复训练过程中，若因患者肌肉张力过高导致无法完成康复训练，而机器人仍然按照原轨迹继续运动，可能导致患者的二次损伤。因此，在被动康复训练过程中增加柔顺性是很有必要的。本文用到的是基于位置控制的阻抗控制器。

常用的阻抗控制数学模型通常用式（7）表示。

M d ∆ x ¨ + B d ∆ x ˙ + K d ∆ x = U (t)

（7）

定义状态变量

z 1 = x

，

z 2 = x ˙

，则系统的状态空间方程为

z ˙ 1 = z 2 z ˙ 2 = 1 M d U t - B d M d z 2 - K d M d z 1

（8）

即

z ˙ 1 z ˙ 2 = 01 - K d M d - B d M d z 1 z 2 + 0 1 M d U t 9

系统随时间的变化公式为

y = 10 z 1 z 2 + 0 U t

（10）

其中：阻抗参数

B d

、

K d

根据不同外部环境的变化而变化，参数调整可描述为：当机器人末端受到外部干扰的影响较大时，认为机器人需要更低的刚度参数和更高的阻尼参数；当机器人末端所受干扰较小时，认为机器人需要更高的刚度参数和更低的阻尼参数。质量参数则根据机械系统质量计算得到。

本文基于上肢康复机器人的末端力传感器，使用外力反馈调整阻尼系数和弹性系数，同时对障碍物和外力进行避让。其核心思想是当接触力在当前速度方向上增大时，可以认为外部环境和人期望在该方向加速运动，所以阻抗系统应该减少阻抗系数，使得机器人产生更大的偏移。反之，当接触力在当前速度方向上减小时，可以认为外部环境和人期望在该方向减速运动，所以阻抗系统应该增大阻抗系数，使得机器人产生较小的偏移。为了提高机器人柔顺性和稳定性，需要将阻抗模型设置在临界阻尼状态下^［19］。所以

B / 2 M K = 1

（11）

阻抗模型阻抗参数调整公式为

B d = B 0 - S

（12）

S = α s g n x ˙ U t

（13）

式中：

α

为常数；

U t

为机器人末端压力。

阻抗模型刚度参数调整公式为

K d = B d 2 4 M d

（14）

式中：

M d = 2

至此，DULLR的自适应柔顺性控制器设计完成。

从图4可以看出，当目标轨迹输入后，内环模糊PID位置控制器进行目标轨迹跟踪。完整过程如下：整个系统的偏差

e x d

经过微分计算得到

e ˙ x d

，

e ˙ x d

模糊PID控制器获得被控对象的目标速度

x ˙ d

，被控对象的目标速度

x ˙ d

经过机器人雅可比矩阵得到每个电机的转速

u

。被控对象完成运动输出

x ˙ r

，

x ˙ r

经过积分计算得到

x r

。在外环自适应柔顺性控制器中，根据末端力传感器的数值变化自动调节阻抗参数，同时对目标轨迹进行位置修正。完整过程如下：当末端力传感器采集到信息后经过处理，首先会经过式（13）得到S，再经过式（12）得到

B d

，

B d

代入式（14）得到

K d

，然后经过阻抗计算模型得到位置偏差，代入到内环位置控制器中。

显示原图|下载原图ZIP|生成PPT

图4 基于位置闭环的自适应柔顺性控制器

3 仿真

根据提出的自适应柔顺性控制器进行仿真验证，在MATLAB/Simulik搭建上肢康复机器人自适应柔顺性控制器模型。对于位置控制器仿真模型，再经过DULLR运动学模型和雅可比矩阵计算，可以将机器人位置信息转化为电机转速，最后经过逆运动学反馈给模糊PID控制器。

模糊控制器仿真使用Fuzzy logic模块，输入隶属度函数选择高斯型，输出隶属度函数选择三角形。根据模糊规则表给控制器添加模糊规则，在模糊控制器调节下，参数输出变量随着2个输入变量的调节过程如图5所示。

显示原图|下载原图ZIP|生成PPT

图5 PID参数调节过程

图6为PID控制器和模糊PID控制的响应曲线，从图6可以看出，模糊PID控制器在上肢康复机器人模型下的响应曲线优于PID控制，其响应时间更短、稳态误差更小。

显示原图|下载原图ZIP|生成PPT

图6 PID控制器和模糊PID控制器阶跃响应曲线

柔顺性控制器在有外力干扰情况下实际输出位置与没有外力干扰情况下实际输出位置与期望输出位置的变化曲线如图7所示。

显示原图|下载原图ZIP|生成PPT

图7 位置变化曲线

如图7所示，红色轨迹为目标轨迹，黑色轨迹为无外力干扰时DULLR的运行轨迹，绿色为有外力干扰时DULLR的运行轨迹。从图7可以看出，在无外力干扰时基于位置闭环的自适应柔顺性控制器轨迹跟踪性能较好，理论上能较好地完成无干扰环境下的被动康复训练。当有外力干扰时，机器人运行到黑色箭头位置时，在机器人末端施加一个外力，当控制器接收到压力信号时通过调整位置减小压力，直到外力干扰消失，机器人会停下等待用户排除干扰并选择是否继续训练。从图7中可以看出，基于位置闭环的自适应柔顺性控制器具有一定的柔顺效果，可以解决患者在训练过程中受到二次伤害的问题。

通过仿真验证，基于压力传感器的自适应柔顺性控制器满足上肢康复机器人的被动康复训练需求。

4 实验

为了验证无外力干扰下控制器的轨迹跟踪能力，设计了轨迹跟踪训练实验，实验过程如图8所示。从图8可以看出，在无干扰情况时，本文设计的控制器具有较好的轨迹跟踪能力。

显示原图|下载原图ZIP|生成PPT

图8 无外力干扰下上肢机器人的轨迹跟踪训练实验

完成无干扰被动康复训练验证后，进行了有外力干扰下上肢机器人的圆周轨迹运动实验。在跟踪过程中，人为增加一个一维的外力干扰，然后撤出外力干扰，实验过程如图9所示。

显示原图|下载原图ZIP|生成PPT

图9 有外力干扰下上肢机器人的圆周轨迹运动状态

图9为有外力干扰下上肢机器人圆周轨迹运动状态，其中白色为目标轨迹，黄色为实际轨迹。从图9b可以看出，在康复训练过程初期没有外力干扰情况时，机器人对圆形轨迹有较好的跟踪效果。从图9d可以看出，在有外力干扰情况下，机器人会顺着力的方向进行偏移直到力消失。图9e为力消失的瞬间，当力消失后压力传感器读数在合理范围时，机器人会停止运动，等待用户排除干扰，选择是否重新进行训练。从实验可以看出上肢康复机器人具有较好的柔顺性效果。

图10为实验过程中压力传感器的实际接触力变化曲线图。

显示原图|下载原图ZIP|生成PPT

图10 接触力变化曲线

5 结论

本文基于DULLR的运动学模型，提出了一种基于位置闭环的自适应柔顺性控制器，利用仿真分析和实验验证了基于位置闭环的自适应柔顺性控制器的有效性和优越性。

（1）模糊PID位置控制器充分考虑了DULLR的运动学模型和速度雅可比矩阵，将其与柔顺性控制器结合，具有较好的轨迹跟踪能力的同时表现出了一定的柔顺性效果。

（2）相较于传统的PID控制器，基于模糊PID的位置控制方法响应时间更短、稳态误差更小，体现出了较好的轨迹跟踪能力。

（3）自适应柔顺性控制与模糊PID位置控制相对独立，能有效完成康复任务的同时防止偏瘫患者在康复训练过程中二次受伤。自适应柔顺性控制比固定阻抗参数的柔顺性能表现出对环境更好的适应性，提高了患者康复训练过程中的舒适度。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	Collaborators G N.Global，regional，and national burden of neurological disorders，1990-2016：a systematic analysis for the global burden of disease study 2016［J］.The Lancet Neurology，2019，18（5）：459-480.

2	中华医学会神经病学分会神经康复学组，中华医学会神经病学分会脑血管病学组，卫生部脑卒中筛查与防治工程委员会办公室.中国脑卒中康复治疗指南（2011完全版）［J］.中国医学前沿杂志，2012，4（6）：55-76.

3	李翠凡，张晗，曹迎东.早期康复训练对脑卒中患者肢体功能恢复的影响［J］.课程教育研究，2019（38）：250，252.

4	孙长城，王春方，丁晓晶，等.上肢康复机器人辅助训练对脑卒中偏瘫患者上肢运动功能的影响［J］.中国康复医学杂志，2018，33（10）：1162-1167.

5	Maples J， Becker J.Experiments in force control of robotic manipulators［C］//Proceedings of 1986 IEEE International Conference on Robotics and Automation.San Francisco：IEEE，1986：695-702.

6	Santos W M， Siqueira A A G.Optimal impedance via model predictive control for robot-aided rehabilitation［J］.Control Engineering Practice，2019，93：104177.

7	Huo W G， Mohammed S， Amirat Y.Impedance reduction control of a knee joint human-exoskeleton system［J］.IEEE Transactions on Control Systems Technology，2019，27（6）：2541-2556.

8	Sado F， Yap H J， Ghazilla R A R，et al.Exoskele-ton robot control for synchronous walking assistance in repetitive manual handling works based on dual unscented Kalman filter［J］.PLoS One，2018，13（7）：200193.

9	Huq R， Lu E， Wang R，et al.Development of a portable robot and graphical user interface for haptic rehabilitation exercise［C］//2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics.Rome：IEEE，2012：1451-1457.

10	王壮，王轶钊，丘世因，等.脑卒中上肢康复机器人研究进展［J］.中国现代神经疾病杂志，2023，23（1）：15-21.

11	Roveda L， Testa A， Ali Shahid A，et al.Q-Learning-based model predictive variable impe-dance control for physical human-robot collaboration［J］.Artificial Intelligence，2022，312：103771.

12	Mujica M， Crespo M， Benoussaad M，et al.Robust variable admittance control for human-robot co-manipulation of objects with unknown load［J］.Robotics and Computer-Integrated Manufacturing，2023，79：102408.

13	Zhong Y C， Wang T， Pu Y F，et al.An adaptive bilateral impedance control based on nonlinear disturbance observer for different flexible targets grasping［J］.Computers and Electrical Enginee-ring，2022，103：108388.

14	Foroutannia A， Akbarzadeh-T M R， Akbarzadeh A，et al.Adaptive fuzzy impedance control of exoskeleton robots with electromyography-based convolutional neural networks for human intended trajectory estimation［J］.Mechatronics，2023，91：102952.

15	Tao G H， Chen L， Ye C L，et al.Design of a desktop upper limb rehabilitation robot［C］//2023 IEEE International Conference on Mechatronics and Automation.Harbin：IEEE，2023：911-916.

16	叶长龙，佟泽卉，于苏洋，等.全方位移动装配机器人运动学分析［J］.机器人，2016，38（5）：550-556.

17	Deboon B， Foley R C A， Nokleby S，et al.Nine degree-of-freedom kinematic modeling of the upper-limb complex for constrained workspace evaluation［J］.Journal of Biomechanical Engineering，2021，143（2）：021009.

18	Cao G Q， Zhao X Y， Ye C L，et al.Fuzzy adaptive PID control method for multi-mecanum-wheeled mobile robot［J］.Journal of Mechanical Science and Technology，2022，36（4）：2019-2029.

19	王杰静.桌面式上肢康复机器人控制系统的设计与实现［D］.上海：上海师范大学，2018.

Options

文章导航

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PB	PM	PM	PS	ZO	ZO
NM	PB	PB	PM	PS	PS	ZO	NS
NS	PM	PM	PM	PS	ZO	NS	NS
ZO	PM	PM	PS	ZO	NS	NM	NM
PS	PS	PS	ZO	NS	NS	NM	NM
PM	PS	ZO	NS	NM	NM	NM	NB
PB	ZO	ZO	NM	NM	NM	NB	NB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NM	NM	NM	ZO	ZO
NM	NB	NM	NM	NM	NS	ZO	PS
NS	NM	NM	NS	NS	ZO	PS	PS
ZO	NM	NM	NS	ZO	PS	PM	PM
PS	NS	NS	ZO	PS	PM	PM	PM
PM	NS	ZO	PS	PS	PM	PB	PB
PB	ZO	ZO	PS	PM	PM	PB	PB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PS	NS	NB	NB	NB	NM	PS
NM	PS	NS	NB	NM	NM	NS	ZO
NS	ZO	NS	NM	NM	NS	NS	ZO
ZO	ZO	NS	NS	NS	NS	NS	ZO
PS	ZO	ZO	ZO	ZO	ZO	ZO	ZO
PM	PB	NS	PS	PS	PS	PS	PB
PB	PB	PM	PM	PM	PS	PS	PB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PB	PM	PM	PS	ZO	ZO
NM	PB	PB	PM	PS	PS	ZO	NS
NS	PM	PM	PM	PS	ZO	NS	NS
ZO	PM	PM	PS	ZO	NS	NM	NM
PS	PS	PS	ZO	NS	NS	NM	NM
PM	PS	ZO	NS	NM	NM	NM	NB
PB	ZO	ZO	NM	NM	NM	NB	NB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NM	NM	NM	ZO	ZO
NM	NB	NM	NM	NM	NS	ZO	PS
NS	NM	NM	NS	NS	ZO	PS	PS
ZO	NM	NM	NS	ZO	PS	PM	PM
PS	NS	NS	ZO	PS	PM	PM	PM
PM	NS	ZO	PS	PS	PM	PB	PB
PB	ZO	ZO	PS	PM	PM	PB	PB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PS	NS	NB	NB	NB	NM	PS
NM	PS	NS	NB	NM	NM	NS	ZO
NS	ZO	NS	NM	NM	NS	NS	ZO
ZO	ZO	NS	NS	NS	NS	NS	ZO
PS	ZO	ZO	ZO	ZO	ZO	ZO	ZO
PM	PB	NS	PS	PS	PS	PS	PB
PB	PB	PM	PM	PM	PS	PS	PB

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 上肢康复机器人系统分析

1.1 机器人结构简介

图1 桌面式上肢康复机器人机械结构图

1.2 上肢康复机器人的运动学模型

图2 DULLR坐标系定义图

2 基于位置闭环的自适应柔顺性控制器设计

2.1 基于模糊PID的位置控制器设计

图3 基于模糊PID的位置控制框图

表1 Kp 的模糊控制规则

表2 Ki 的模糊控制规则

表3 Kd 的模糊控制规则

2.2 自适应柔顺性控制器设计

图4 基于位置闭环的自适应柔顺性控制器

3 仿真

图5 PID参数调节过程

图6 PID控制器和模糊PID控制器阶跃响应曲线

图7 位置变化曲线

4 实验

图8 无外力干扰下上肢机器人的轨迹跟踪训练实验

图9 有外力干扰下上肢机器人的圆周轨迹运动状态

图10 接触力变化曲线

5 结论

参考文献

表1 K_p 的模糊控制规则

表2 K_i 的模糊控制规则

表3 K_d 的模糊控制规则

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PB	PM	PM	PS	ZO	ZO
NM	PB	PB	PM	PS	PS	ZO	NS
NS	PM	PM	PM	PS	ZO	NS	NS
ZO	PM	PM	PS	ZO	NS	NM	NM
PS	PS	PS	ZO	NS	NS	NM	NM
PM	PS	ZO	NS	NM	NM	NM	NB
PB	ZO	ZO	NM	NM	NM	NB	NB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	NB	NB	NM	NM	NM	ZO	ZO
NM	NB	NM	NM	NM	NS	ZO	PS
NS	NM	NM	NS	NS	ZO	PS	PS
ZO	NM	NM	NS	ZO	PS	PM	PM
PS	NS	NS	ZO	PS	PM	PM	PM
PM	NS	ZO	PS	PS	PM	PB	PB
PB	ZO	ZO	PS	PM	PM	PB	PB

E	EC
E	NB	NM	NS	ZO	PS	PM	PB
NB	PS	NS	NB	NB	NB	NM	PS
NM	PS	NS	NB	NM	NM	NS	ZO
NS	ZO	NS	NM	NM	NS	NS	ZO
ZO	ZO	NS	NS	NS	NS	NS	ZO
PS	ZO	ZO	ZO	ZO	ZO	ZO	ZO
PM	PB	NS	PS	PS	PS	PS	PB
PB	PB	PM	PM	PM	PS	PS	PB