协作机器人是一种能够与人类在生产线上协同作业的新型工业机器人,它结合了机器人的效率与人类的智慧,具有高性价比、智能、安全等优点
[1]。随着协作机器人在智能制造领域的广泛应用,精确高效的轨迹规划算法变得至关重要
[2]。本文以汽车部件喷漆任务为背景,研究协作机器人的喷漆轨迹规划问题,旨在提高生产效率、降低人力成本并改善喷漆质量。
近年来,许多学者致力于研究协作机器人的喷漆轨迹规划算法。Zhou等
[3]提出了一种基于圆柱体的喷涂模型,通过将复杂曲面逼近为简单的圆柱,并结合Beta分布模型和微分几何原理进行轨迹规划。Chen等
[4]使用平面片邻接图(flat patch adjacency graph,FPAG)方法对3D实体进行分片,并在每个分片上规划喷漆路径,然后通过改进的智能优化算法解决了喷漆轨迹的最优集成问题。Jan等
[5]提出一种基于最小生成树和三角网格的轨迹规划方法,并通过三角形合并策略减少了喷涂过程中的转弯次数。Li等
[6]提出一种基于漆膜厚度均匀性的轨迹规划方法,并设计首尾变速缓冲区以实现匀速喷涂,但其主要针对于平面件,难以适应复杂曲面。此外,上述算法大多基于计算机辅助设计(computer aided design,CAD)模型、网格模型或普通数学模型,对于复杂曲面建模有一定困难,数据特征识别也存在挑战。
随着激光扫描仪的发展,研究者开始利用点云数据进行喷漆轨迹规划。Chen等
[7]利用点云切片方法求解工件表面的路径信息,但由于使用了手动区域分割,在一定程度上影响了结果的准确性和一致性。Gleeson等
[8]在此基础上将轨迹段的位置和时间长度作为优化变量,进一步提升轨迹精度。Tiboni等
[9]提出了端到端的深度学习网络PaintNet,将点云模型作为输入,输出喷涂位姿序列,但该网络在稳定性和可迁移性方面仍存在问题。此外,Tadic等
[10]、Tasnim等
[11]和Gülırmak等
[12]等尝试在硬件上加以改进,使用不同精度的激光相机进行建模并优化喷枪控制算法,但并未对初始轨迹规划算法进行改进。Yu等
[13]提出一种自动化点云切片算法,可自主确定切片方向并进行轨迹规划。但由于需要在切片两端进行最近点对搜索,其算法复杂度较高。Lu等
[14]根据点云法向量的分量将模型进行分割,并在子部分上进行切片,近似得到喷涂路径。但对于曲率变化大的自由曲面,会损失更多细节特征。此外,现有算法中使用的切片方式复杂度过高,且其中的插补算法只适用于形状相对规则的表面,使复杂曲面轨迹精度显著降低。
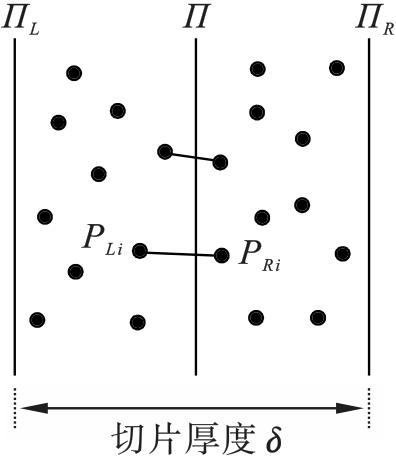
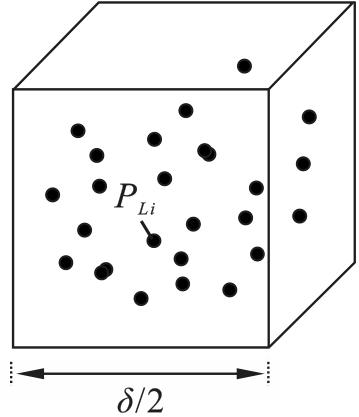
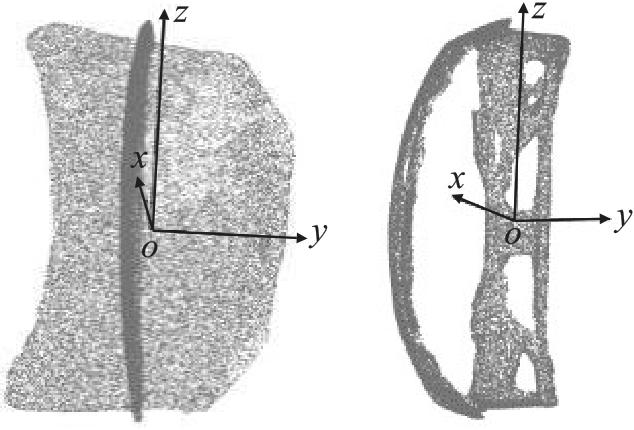
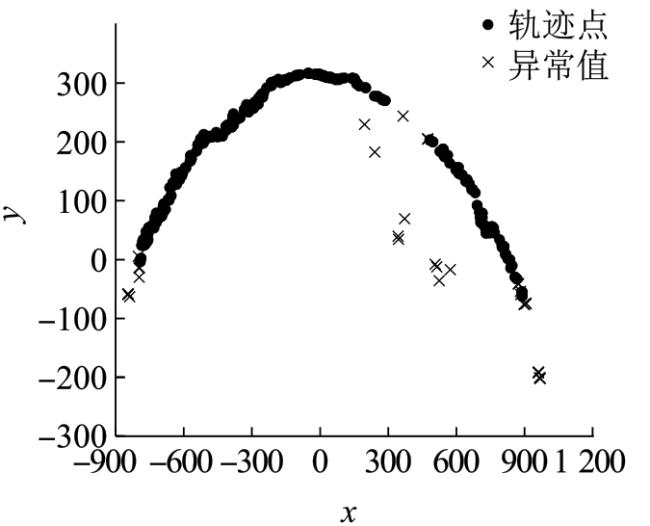
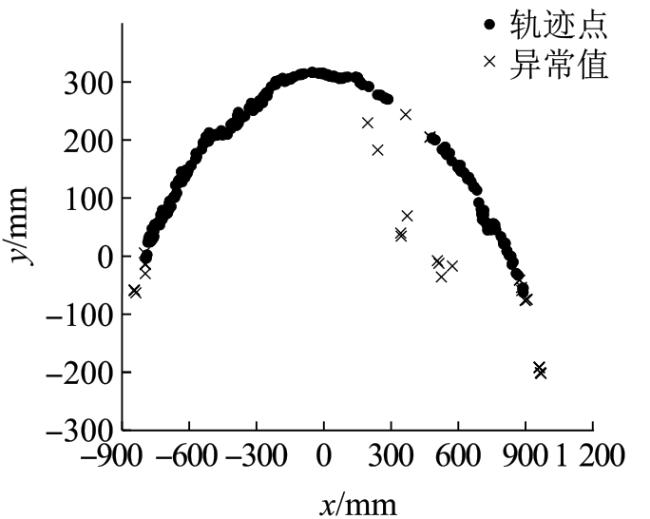
对此,本文根据重建后的点云模型稀疏性选取合适的切片阈值,提出一种点云薄切算法,通过避免最近点对的搜索过程提升算法的效率。在得到初始轨迹点的同时,将其合理映射到二维坐标系中进行处理。随后通过引入孤立森林
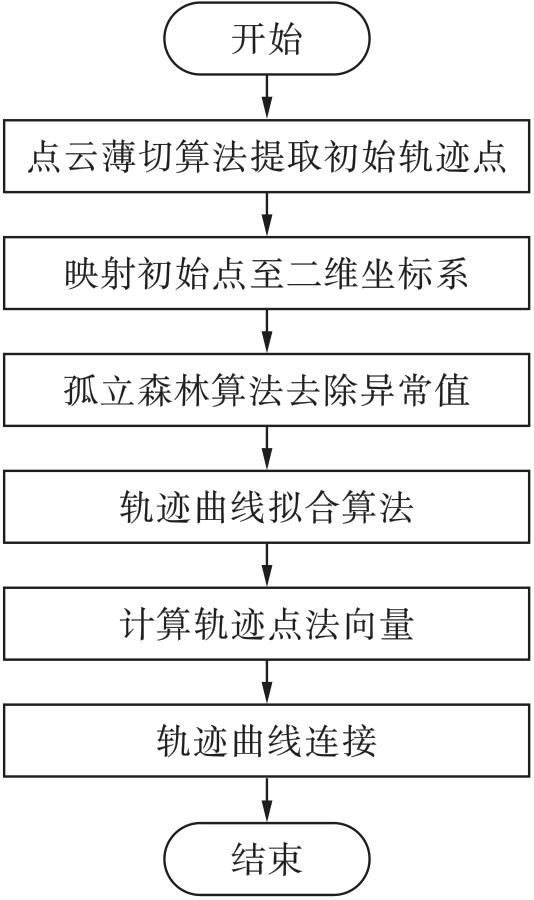
[15](isolation forest,Iforest)算法去除初始轨迹点异常值,并结合多项式拟合方法对轨迹进行曲线拟合。最后根据一定的步长选取机器人运动的轨迹点,并通过计算轨迹点法向量来确定喷头的具体姿态。算法流程图如
图1所示,实验表明该算法的运行速度更快,生成轨迹的精度和光滑度更高。