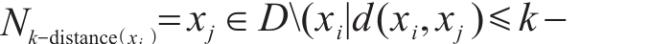基于局部离群因子的模糊支持向量机算法

张庆宝; 鞠哲; 张万里

doi:10.3969/j.issn.2095-1248.2024.06.010

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 6: 90 - 96

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.06.010

基础科学与工程

基于局部离群因子的模糊支持向量机算法

张庆宝 ,
鞠哲 ,
张万里

展开

沈阳航空航天大学理学院，沈阳 110136

张庆宝（1998-），男，河南南阳人，硕士研究生，主要研究方向：机器学习，E-mail：775598161@qq.com

鞠哲（1986-），男，辽宁营口人，副教授，博士，主要研究方向：机器学习、生物信息学，E-mail：juzhe1120@hotmail.com。

收稿日期: 2024-03-30

网络出版日期: 2025-02-05

基金资助

国家重点研发计划子项(2019YFC1903901-01)

收起

Fuzzy support vector machine algorithm based on local outliers factor

Qingbao ZHANG ,
Zhe JU ,
Wanli ZHANG

Expand

College of Science，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2024-03-30

Online published: 2025-02-05

Fold

摘要

模糊支持向量机是一种结合了支持向量机和模糊理论的分类算法。现有的模糊支持向量机算法可以在一定程度上克服噪声数据的影响，但存在成本敏感性，导致对数据的先验分布估计不准确。提出一种新的模糊支持向量机算法，该算法在设计样本的模糊隶属度函数时，利用采样点及其邻域密度的相似性构建的离群因子来更好地获取数据的分布信息。利用UCI数据集对优化后的模型进行验证，证明了其良好的性能。

关键词： 模糊支持向量机; 邻域密度; 离群因子; 隶属度函数; 不平衡数据

本文引用格式

张庆宝 , 鞠哲 , 张万里 . 基于局部离群因子的模糊支持向量机算法[J]. 沈阳航空航天大学学报, 2024 , 41(6) : 90 -96 . DOI: 10.3969/j.issn.2095-1248.2024.06.010

Abstract

Fuzzy support vector machine is a classification algorithm that combines support vector machine and fuzzy theory.The existing fuzzy support vector machine algorithms can overcome the impact of noise data to some extent，but they have cost sensitivity，leading to inaccurate estimation of the prior distribution of data.A new fuzzy support vector machine algorithm was proposed.When designing the fuzzy membership function of samples，this algorithm better captures the distribution information of data by using the outlier factor constructed by the similarity of sampling points and their neighborhood density.The optimized model is validated using UCI datasets，which proves its good performance.

Key words： fuzzy support vector machine; neighborhood density; outlier factor; membership function; imbalanced dataset

支持向量机（support vector machine，SVM）是一种基于统计学的VC（Vapnik Chervonenkis）维理论和结构风险最小化原理的机器学习方法，能较好地解决小样本、非线性、局部极小等实际问题，在模式识别和分类问题上具有良好的泛化性能。然而SVM对于噪声和异常值较为敏感，在产生分类决策面时易受其影响。Lin等^［1］将模糊数学的概念引入到SVM中，提出了模糊支持向量机（fuzzy support vector machine，FSVM）算法，通过对每个样本赋予一个模糊隶属值，使得不同的样本在构造分类决策面时的贡献不同。FSVM是一种代价敏感算法，可以在一定程度上克服噪声数据的影响，但是该算法不能有效地处理不平衡数据上的分类问题，该算法的隶属度计算仅依赖于原始数据空间中的中心点和初始超平面，可以很好地识别规则的单密集区域数据。然而，由于过度依赖中心点的计算，该算法在面对不规则或多个数据密集型区域时性能较差，一些改进的FSVM算法被相继提出。Fu等^［2］提出了一种新的基于相对密度的直觉模糊支持向量机（relative density-based intuition istic FSVM，RIFSVM）算法。利用相对密度来获取样本的先验信息，并通过引入直觉模糊评分函数进一步提高了模型对噪声或离群点的强识别能力，降低了类不平衡的影响。Kumar等^［3］提出了一种基于类内密度信息的模糊支持向量机（FSVM with within-class density information，FSVM-WD）算法，使用k近邻距离的概念来估计类内相对密度，样本的隶属度被定义为k近邻距离的倒数，具有较高的鲁棒性和容错性。Liu等^［4］提出了一种基于支持向量数据描述（support vector data description，SVDD）的模糊支持向量机算法（SVDD-based FSVM，FSVM-SVDD），噪声和异常点是由一个体积最小且包含最多样本的超球体来识别的，比SVM和FSVM具有更强的鲁棒性。Fan等^［5］提出了一种基于样本类确定性的模糊隶属度评价方法（entropy-based FSVM，EFSVM），利用熵来评价训练样本的类确定性，然后根据训练样本的类确定性来分配它们的模糊隶属度。与传统的 SVM 和 FSVM 相比，EFSVM 在不平衡数据集上能得到更灵活的决策面。Zhang等^［6］将信息熵与归一化的类中心距离相结合，得到模糊隶属函数，其中信息熵是基于k近邻（k-nearest neighbors，KNN）算法计算的。罗富财等^［7］将数据局部密度和数据特征距离引入模糊聚类，并将聚类得到的模糊隶属度作为模糊因子应用于模糊支持向量机，降低了人为选取模糊因子的主观性，将噪声点和孤立点对分类造成的影响降至最低。该方法使用KNN算法根据样本点之间的距离确定样本的局部密度。

上述算法采用KNN算法选择近邻点时，通常使用欧氏距离或曼哈顿距离等标准来度量样本点之间的距离，从而确定样本之间的紧密度。这种方法在分类和回归问题中表现出色，尤其在样本分布均匀且类别界限清晰的情况下。然而，KNN算法在处理密度分散不均的数据时可能会遇到一些困难。当数据中存在不同密度的类簇时，使用统一的距离度量标准可能无法准确反映样本之间的真实紧密度。此外，KNN算法对噪声和异常值也比较敏感，因为它们可能会改变样本点之间的距离分布。对此，本文结合了文献［8—13］的异常数据识别方法，在设计模糊隶属函数时利用采样点及其邻域密度的相似性构建的离群因子（local outlier factor，LOF）获取数据的分布特征。相比之下，LOF算法关注的是每个样本点相对于其近邻点的局部密度偏差。因此，即使在不同密度的类簇中，LOF算法也能有效地识别出异常值和离群点。

1 模糊支持向量机

在处理噪声和异常值时，SVM对每个样本同等对待，每个样本的误分类成本是相同的，使得决策表面有很大的偏差^［9］。FSVM在其目标函数中考虑了每个样本对一个类的模糊归属，通过引入模糊隶属度来区分不同样本的重要性。假设一个二分类数据集

D = {(x 1, y 1), (x 2, y 2), ⋯, (x n, y n)}

，引入模糊隶属度，数据集被扩展为

D = {(x 1, y 1, s 1),

(x 2, y 2, s 2), ⋯,

(x n, y n, s n)}

，

s i

为第

i

个样本的模糊隶属度；

x i ∈ R n

；y_i

∈

- 1,1

。与SVM不同，FSVM首先将输入空间中的样本点映射到高维特征空间中，然后通过求解二次规划问题得到分类超平面。其目标函数可以表示为

m i n ω, b 12 ω 2 + C ∑ i = 1 n s i ξ i

（1）

式中：

C > 0

是惩罚参数；

ξ i

为第

i

个样本点的松弛变量；

n

为样本数；

s i

为样本点

x i

的模糊隶属值。

约束条件为

y i (ω ⋅ φ (x) + b) ≥ 1 - ξ i, ξ i ≥ 0, i = 1,2, ⋯, n

（2）

式中：

y i

为第

i

个样本的标签；

φ (x i)

为将输入空间中的数据映射到特征空间中的向量；

b

为偏差。

为求解式（1），通过拉格朗日函数求其对偶规划为

m a x ω (α) = ∑ i = 1 n α i - 12 ∑ i = 1 n ∑ j = 1 n α i α j y i y j k (x i, x j)

（3）

约束条件为

∑ i = 1 n α i y i = 0,0 ≤ α i ≤ C s i, i = 1,2, ⋯, n

（4）

在对偶问题中，变量

α i

的上界约束随着模糊因子

s i

变化。所以模糊隶属度

s i

成为决定FSVM性能好坏的关键。

2 基于类中心的模糊隶属函数的局限性

本文在一个人工数据集上分析了基于类中心距离的模糊隶属度计算方法的局限性。图1a是一个外部密集、内部稀疏的二维人工数据集，按照Lin等^［1］的方法，外围样本将会被赋予较小的模糊隶属值，结果如图1b所示。显然，基于样本到类中心距离的方法无法准确描述数据的分布特征，密集区域的样本很可能被分配一个相对较小的权重。对于实际情况而言，同一类别的距离类中心距离相同的两个样本，一个在高密度区域，一个在相对稀疏的区域，显然前者更重要。

显示原图|下载原图ZIP|生成PPT

图 1 人工数据集上一些实例的模糊隶属度值

现有的改进模糊支持向量机算法虽然考虑到样本周围的紧密度（文献［2—7］），但通常是根据样本点之间的距离确定的，这在处理密度分散不均的数据时，可能无法准确反映样本之间的真实紧密程度。此外，噪声和异常值的存在可能会改变样本点之间的距离分布。为了更好地解决这些问题，本文将样本的离群因子作为设计模糊隶属函数的依据。

3 局部离群因子的定义

3.1 实例的k距离邻域

假设

x i ∈ D

，对于

∀ k ∈ Z

，点

x i

的

k

距离记为k-distance（x_i ），它表示点

x i

到第

k

个近邻点的距离，但不包括点

x i

。对于

x j ∈ D

，

x j

与

x i

的距离记为

d (x i, x j)

。给定点

x i

的

k

距离，则点

x i

的

k

距离邻域包括与点

x i

的距离不超过

k

距离的所有点，定义为

k - d i s t a n c e (x i)

，简记为

N k (x i)

，计算如下。

显示原图|下载原图ZIP|生成PPT

（5）

式中：点

x j

称为点

x i

的

k

最近邻^［14-16］。

3.2 局部可达密度

点

x i

的局部可达密度被定义为

l r d k (x i) = N k (x i) ∑ x j ∈ N k (x i) r e a c h - d i s t k (x i, x j)

（6）

式中：

r e a c h - d i s t k (x i, x j) = m a x

k-distance（x_j ）

d (x i, x j)}

为

x i

、

x j

两点间的可达距离，偏离程度较大的点的可达距离之和一般大于偏离程度较小的点的可达距离之和，那么局部可达密度要小于偏离程度较小的点的局部可达密度。

l r d k (x i)

值说明了点所处的局部空间区域的密度情况^［14-16］。

3.3 局部离群因子

点

x i

的LOF定义为

L O F k (x i) = ∑ x j ∈ N k (x i) l r d k (x j) l r d k (x i) N k (x i)

（7）

式（7）表示相邻实例

N k (x i)

的局部可达密度与实例

x i

的局部可达密度之比的平均值。如果这个比率更接近于1，那么它表示在

x i

的邻域内的实例密度相似，且

x i

可能与该邻域属于同一聚类。如果比值小于1，表示

x i

密度大于其邻域点密度，

x i

密度大；如果该比值大于1，表示

x i

的密度小于其邻近实例的密度，则

x i

更有可能是一个离群值。不难看出，若点

x i

的偏离程度较大，则它的局部可达密度

l r d k (x i)

较小，而它的

N k (x i)

内的点由于处在同一个群组中，那么它们的局部可达密度

l r d k (x i)

相对较小，则

l r d k (x j) / l r d k (x i)

的值较大，最终点

x i

的LOF值就越大，它离周围的实例就越远^［14-16］。

3.4 基于离群因子的模糊隶属函数设计

基于样本的离群因子，本文的模糊隶属函数定义为

s i + = 1, i = 1,2, ⋯, p

（8）

s i - = 1 1 + e x p (L O F i -), i = p + 1, p + 2, ⋯, n

（9）

式中：

L O F i -

为第

i

个负类样本的局部离群因子。

为了探究式（9）的合理性，使用式（9）计算并标记出与图1b相同的30个实例的模糊隶属值，结果如图2所示。在图2中，很明显，外围实例和内部实例的模糊隶属值并不像图1b所示的相隔甚远。相反，它遵循实例的分布特征，将较小的模糊值分配给分布在稀疏区域的样本点，将较大的模糊值分配给分布在密集区域的样本点。从图2可以看出，边缘上的实例没有被误判为噪声，并给出了合理的模糊值。从图2可以看出，对于这种非正态分布的数据集，本文的模糊隶属值计算方法是比较合理的。

显示原图|下载原图ZIP|生成PPT

图 2 用LOF计算人工数据集上一些实例的模糊隶属值

4 数据验证

为了进一步分析和评估本文算法对分类任务的贡献是否仅限于特定数据集，将研究范围扩大。本文采用UCI数据库中的多个二分类数据集进行初步测试，UCI数据集及其相关属性，如表1所示。Libsvm-weight-3.20软件包用来训练FSVM模型，为每个样本分配不同的权值。所有数值实验均在

2.50 G H z / 8.0 G B

的计算机上利用Matlab2023b软件实现。

表1 UCI数据集及其相关属性

数据集	属性数	样本数	不平衡比	少数类	多数类
teaching	5	151	2.08	Class1	Class2，3
hepatitis	19	155	3.84	Class1	Class2
Ecoli	7	272	4.23	class3	Class1，2
Yeast	8	514	9.09	Class5	Class1
chess-krvk-1	6	276	2.54	class3	Class6
chess-krvk-3	6	2 994	14.14	Class6	Class1
chess-krvk-4	6	2 012	73.52	Class2	Class12

为了有效地评估模型的分类性能，采取以下评估指标：AUC、G-mean和F1值。这些评估指标都是基于一个混淆矩阵，如表2所示。

表2 混淆矩阵

实际类别	预测类别
实际类别	正类	负类
正类	$T P (T r u e P o s i t i v e)$	$F N (F a l s e N e g a t i v e)$
负类	$F P (F a l s e P o s i t i v e)$	$T N (T r u e N e g a t i v e)$

Precision

= T P T P + F P

（10）

Recacall

= T P T P + F N

（11）

G - m e a n = P r e c i s i o n · R e c a l l

（12）

F 1 = 2 · P r e c i s i o n · R e c a l l P r e c i s i o n + R e c a l l

（13）

实验中所有SVM和FSVM算法均采用RBF核函数，使用网格搜索法对惩罚因子

C

和核参数

γ

进行选择，

C

的选择范围是

[20, 215]

，

γ

的选择范围是

[2 - 15, 20]

。在计算LOF值时，本文根据数据集的大小指定了参数

k

的取值范围：

k = N

，

N

为样本数。本文算法与5种模糊支持向量机算法的比较结果如表3—9所示。

表3 在teaching数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.758 1±0.019 9	0.676 5±0.025 2	0.576 5±0.031 4
RIFSVM	0.759 2±0.028 5	0.728 5±0.025 5	0.640 2±0.030 0
FSVM-WD	0.773 6±0.019 4	0.705 6±0.015 2	0.608 0±0.018 4
FSVM-SVDD	0.767 7±0.021 3	0.675 1±0.028 0	0.571 9±0.034 6
EFSVM	0.768 7±0.028 4	0.710 9±0.028 7	0.603 7±0.034 8
LOF-FSVM	0.777 4±0.023 7	0.738 4±0.028 9	0.660 7±0.029 4

表4 在hepatitis数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.849 7±0.011 8	0.474 9±0.047 3	0.355 8±0.058 3
RIFSVM	0.866 5±0.010 5	0.772 4±0.026 3	0.618 0±0.034 4
FSVM-WD	0.865 4±0.011 1	0.772 0±0.019 3	0.593 5±0.023 2
FSVM-SVDD	0.860 3±0.013 3	0.343 0±0.066 4	0.213 0±0.072 6
EFSVM	0.865 2±0.015 1	0.666 3±0.028 0	0.537 8±0.035 4
LOF-FSVM	0.871 9±0.010 1	0.810 4±0.017 2	0.644 9±0.023 0

表5 在Ecoli数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.997 2±0.004 2	0.797 7±0.014 7	0.752 6±0.019 3
RIFSVM	0.999 1±0.001 6	0.984 8±0.012 0	0.540 9±0.014 2
FSVM-WD	0.999 8±0.000 3	0.985 3±0.031 7	0.904 6±0.034 8
FSVM-SVDD	0.998 7±0.000 9	0.866 1±0.039 3	0.839 1±0.044 4
EFSVM	0.999 5±0.000 5	0.945 9±0.024 6	0.904 3±0.028 1
LOF-FSVM	1.000 0±0.000 0	0.988 4±0.030 7	0.987 9±0.032 2

表6 在Yeast1数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.975 4±0.001 7	0.837 7±0.006 2	0.765 6±0.013 9
RIFSVM	0.979 9±0.003 4	0.906 2±0.017 3	0.730 6±0.030 1
FSVM-WD	0.979 4±0.001 7	0.896 1±0.008 2	0.706 0±0.011 7
FSVM-SVDD	0.978 8±0.001 3	0.832 7±0.006 7	0.765 5±0.013 0
EFSVM	0.978 7±0.001 3	0.855 3±0.009 2	0.756 9±0.012 8
LOF-FSVM	0.979 9±0.001 7	0.889 8±0.008 4	0.770 5±0.010 9

表7 在chess-krvk-1数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.998 8±0.000 4	0.976 7±0.011 7	0.969 6±0.013 0
RIFSVM	0.998 5±0.000 5	0.986 2±0.006 1	0.980 7±0.007 5
FSVM-WD	0.998 9±0.000 3	0.985 4±0.002 5	0.980 7±0.003 0
FSVM-SVDD	0.998 7±0.000 3	0.984 1±0.001 1	0.979 4±0.002 7
EFSVM	0.998 9±0.000 2	0.984 7±0.002 4	0.980 0±0.003 6
LOF-FSVM	0.999 0±0.000 2	0.988 6±0.002 6	0.982 1±0.004 0

表8 在chess-krvk-3数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.999 6±0.000 3	0.980 1±0.002 7	0.975 9±0.002 8
RIFSVM	0.999 6±0.000 2	0.990 3±0.004 1	0.960 9±0.008 5
FSVM-WD	0.999 7±0.000 1	0.992 1±0.003 0	0.947 2±0.004 5
FSVM-SVDD	0.999 2±0.000 1	0.908 2±0.005 1	0.897 3±0.005 5
EFSVM	0.999 7±0.000 1	0.974 9±0.001 9	0.963 5±0.004 4
LOF-FSVM	0.999 8±0.000 1	0.993 6±0.003 2	0.973 7±0.003 4

表9 在chess-krvk-4数据集上的分类结果

方法	AUC	G-mean	F1
FSVM	0.997 2±0.004 2	0.797 7±0.014 7	0.752 6±0.019 3
RIFSVM	0.999 1±0.001 6	0.984 8±0.012 0	0.540 9±0.014 2
FSVM-WD	0.999 8±0.000 3	0.985 3±0.031 7	0.904 6±0.034 8
FSVM-SVDD	0.998 7±0.000 9	0.866 1±0.039 3	0.839 1±0.044 4
EFSVM	0.999 5±0.000 5	0.945 9±0.024 6	0.904 3±0.028 1
LOF-FSVM	1.000 0±0.000 0	0.988 4±0.030 7	0.987 9±0.032 2

由表3—9的最终结果可以看出，本文算法分类性能提升显著，在AUC、G-mean值和F1值评估指标下均取得了较好的结果。从表3可以看出，FSVM算法的表现比较弱，这是因为数据分布有可能不是标准的球形分布，也可能是异常值的影响。无论是哪一种情况，很显然，这样基于样本到类中心距离来设计的模糊隶属函数会出现问题，样本与类别之间的归属信息无法得到准确的表述。本文算法考虑了样本的局部离群因子（实例

x i

的局部可达密度与相邻实例

N k (x i)

的局部可达密度之比的平均值）。如果LOF值小于1，则表示

x i

的密度大于其邻域点的密度，并且

x i

是致密的；如果LOF值大于1，表明

x i

的密度小于其相邻实例的密度，则

x i

越有可能是离群值。这一过程可以更好地获取数据的分布信息并对模糊隶属函数作出适当的修正，减小了仅使用样本与类中心距离作为模糊隶属函数时对数据集几何形状的依赖，数据集是非球形分布时的分类精度也获得了提升，同时也降低了异常值或噪声点对分类超平面的影响。此外，根据表3—9中的F1值，本文算法在7个数据集中表现出绝对的优势，F1值越高，对少数类的分类准确率就越高，这说明其他7种算法在少数类分类中的性能并不高，这可能是因为这些算法得到的分离超平面仍然向少数类倾斜，导致少数类的分类准确率较低。从最终结果来看，本文算法分类性能不仅优于标准的FSVM算法，而且优于现有的一些改进FSVM算法。基于离群因子的模糊隶属函数设计思路使得每个样本对最终的决策超平面有着相对合理的影响，有效降低了异常数据对最优分类超平面的影响，提高了模型的分类性能。

5 结论

本文算法在设计样本的模糊隶属函数时，利用采样点及其邻域密度的相似性构建的离群因子来获取数据的分布特征。由于LOF算法关注的是局部密度偏差，因此它对异常值和离群点更加敏感。这意味着即使在一个复杂的数据集中，LOF算法也能准确地识别出那些与周围样本点密度差异较大的点。此外，LOF算法不需要假设数据分布是均匀的或具有特定的形状。因此，它可以应用于各种类型的数据集，包括那些具有不同密度类簇的数据集。因此，在处理密度分散不均或存在异常值的数据集时，本文算法更具优越性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	Lin C F， Wang S D.Fuzzy support vector machines［J］.IEEE Transactions on Neural Networks，2002，13（2）：464-471.

2	Fu C， Zhou S S， Zhang D，et al.Relative density-based intuitionistic fuzzy SVM for class imbalance learning［J］.Entropy，2022，25（1）：34.

3	Kumar A， Singh S K， Saxena S，et al.CoMHisP：a novel feature extractor for histopathological image classification based on fuzzy SVM with within-class relative density［J］.IEEE Transactions on Fuzzy Systems，2021，29（1）：103-117.

4	Liu W， Ci L L， Liu L P.A new method of fuzzy support vector machine algorithm for intrusion detection［J］.Applied Sciences，2020，10（3）：1065.

5	Fan Q， Wang Z， Li D D，et al.Entropy-based fuzzy support vector machine for imbalanced datasets［J］.Knowledge-Based Systems，2017，115（3）：87-99.

6	Zhang X Y， Guo Y L， Li F L，et al.Geometric mean maximum FSVMI model and its application in carotid artery stenosis risk prediction［J］.Chinese Journal of Electronics，2021，30（5）：824-832.

7	罗富财，吴飞，陈倩，等.基于机器学习的无线传感器网络入侵检测算法［J］.哈尔滨工程大学学报，2020，41（3）：433-440.

8	徐志博，刘永生，户盼茹.结合离群因子和K-means++聚类改进的点云去噪算法［J］.信息技术与信息化，2023，15（3）：21-24.

9	Wang K F， An J， Yu Z B，et al.Kernel local outlier factor-based fuzzy support vector machine for imbalanced classification［J］.Concurrency and Computation：Practice and Experience，2021，33（13）：62-77.

10	凌莉，程张玉，邹承明.融合孤立森林和局部离群因子的离群点检测方法［J］.计算机应用与软件，2022，39（12）：278-283.

11	She C Y， Zeng S H， Wang Q，et al.Adaptive fuzzy C-means clustering integrated with local outlier factor［J］.Intelligent Data Analysis，2022，26（6）：1507-1521.

12	杨娜，付颖煜，李天昊.基于局部离群因子的数据异常识别方法及其在古建结构监测中的应用［J］.建筑结构学报，2022，43（10）：68-75.

13	Kim M， Jung S， Kim B，et al.Fault detection method via k-nearest neighbor normalization and weight local outlier factor for circulating fluidized bed boiler with multimode process［J］.Energies，2022，15（17）：6146.

14	Breunig M M， Kriegel H P， Ng R T，et al.LOF：identifying density-based local outliers［C］//Proceedings of the 2000 ACM SIGMOD international conference on Management of data.Dallas：ACM，2000：93-104.

15	张付志，魏莎. 基于局部密度的用户概貌攻击检测算法［J］.小型微型计算机系统，2013，34（4）：850-855.

16	周玉，朱文豪，孙红玉.一种基于目标函数的局部离群点检测方法［J］.东北大学学报（自然科学版），2022，43（10）：1405-1412.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 模糊支持向量机

2 基于类中心的模糊隶属函数的局限性

图 1 人工数据集上一些实例的模糊隶属度值

3 局部离群因子的定义

3.1 实例的k距离邻域

3.2 局部可达密度

3.3 局部离群因子

3.4 基于离群因子的模糊隶属函数设计

图 2 用LOF计算人工数据集上一些实例的模糊隶属值

4 数据验证

表1 UCI数据集及其相关属性

表2 混淆矩阵

表3 在teaching数据集上的分类结果

表4 在hepatitis数据集上的分类结果

表5 在Ecoli数据集上的分类结果

表6 在Yeast1数据集上的分类结果

表7 在chess-krvk-1数据集上的分类结果

表8 在chess-krvk-3数据集上的分类结果

表9 在chess-krvk-4数据集上的分类结果

5 结论

参考文献