沈阳航空航天大学学报

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 5: 54 - 61

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.05.006

信息科学与工程

基于全连接神经网络的GNSS/INS组合定位方法

  • 王尔申 , 1a, 1b ,
  • 刘依凡 1a ,
  • 于腾丽 1c ,
  • 杨健 2 ,
  • 刘达 2 ,
  • 张树宁 1c ,
  • 易静怡 1a ,
  • 李昕 1a
展开
  • 1a. 沈阳航空航天大学，电子信息工程学院，沈阳 110136
  • 1b. 沈阳航空航天大学，民用航空学院，沈阳 110136
  • 1c. 沈阳航空航天大学，航空宇航学院，沈阳 110136
  • 2. 辽宁通用航空研究院，沈阳 110136

王尔申（1980-），男，辽宁辽阳人，教授，博士，主要研究方向：北斗卫星导航、多源组合导航技术，E-mail：。

收稿日期: 2024-04-27

  网络出版日期: 2024-12-11

基金资助

国家自然科学基金(62173237)

嵩山实验室预研项目(YYJC062022017)

辽宁省科技厅应用基础研究计划项目(2022020502-JH2/1013)

沈阳市科技局项目(22-322-3-34)

辽宁省教育厅重点攻关项目(LJKZZ20220031)

收起

GNSS/INS integrated positioning method based on fully connected neural network

  • Ershen WANG , 1a, 1b ,
  • Yifan LIU 1a ,
  • Tengli YU 1c ,
  • Jian YANG 2 ,
  • Da LIU 2 ,
  • Shuning ZHANG 1c ,
  • Jingyi YI 1a ,
  • Xin LI 1a
Expand
  • 1a. College of Electronic and Information Engineering，Shenyang 110136，China
  • 1b. College of Aerospace Engineering，Shenyang 110136，China
  • 1c. College of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China
  • 2. Liaoning General Aviation Academy，Shenyang 110136，China

Received date: 2024-04-27

  Online published: 2024-12-11

Fold

摘要

作为一种比单一导航系统精度更高、稳健性更好的导航方案，全球导航卫星系统/惯性导航系统（global navigation satellite system/inertial navigation system，GNSS/INS）组合导航，在各种运动载体中得到广泛应用。针对环境遮挡或电磁干扰导致卫星导航信号中断从而降低组合定位精度的问题，提出一种基于全连接神经网络（fully connected neural network，FCNN）的GNSS/INS组合导航定位方法，该方法由训练模块和预测模块构成。在GNSS信号正常的情况下，该方法利用INS解算的位置和速度信息与组合导航输出的位置和速度信息对FCNN模型进行训练；当GNSS信号中断或失效时，利用前期训练的FCNN模型预测输出导航解。采用实测数据对所提方法进行了验证，结果表明，提出的基于FCNN的GNSS/INS组合导航方法可有效地抑制单一惯导定位误差发散的情况，提高GNSS信号中断时GNSS/INS组合定位结果的精度和可用性。

关键词： 全球导航卫星系统; 惯性导航系统; 信号中断; 组合导航; 全连接神经网络

本文引用格式

王尔申 , 刘依凡 , 于腾丽 , 杨健 , 刘达 , 张树宁 , 易静怡 , 李昕 . 基于全连接神经网络的GNSS/INS组合定位方法[J]. 沈阳航空航天大学学报, 2024 , 41(5) : 54 -61 . DOI: 10.3969/j.issn.2095-1248.2024.05.006

Abstract

As a navigation solution with higher accuracy and better robustness compared to single navigation systems，GNSS/INS integrated navigation has been widely applied in various carriers.Aiming at the problem of the satellite navigation signal interruption caused by environmental obstruction or electromagnetic interference to reduce the accuracy of integrated positioning，GNSS/INS integrated navigation positioning method by a fully connected neural network （FCNN）was proposed.This method consisted of training and prediction modules.Under normal GNSS signal conditions，the me-thod utilized the position and velocity information calculated by INS and the position and velocity information output by the integrated navigation to train the FCNN model.When the GNSS signals were interrupted or fail，the pre-trained FCNN model was used to predict the navigation solutions.Experimental data was employed to validate the proposed method.The results indicate that the GNSS/INS based on FCNN integrated navigation method proposed in this study effectively suppresses the divergence of single INS positioning errors，thereby improving the accuracy and availability of GNSS/INS integra-ted positioning results when the GNSS signals are interrupted.

Key words： global navigation satellite system; inertial navigation system; signal interruption; integra-ted navigation; fully connected neural network

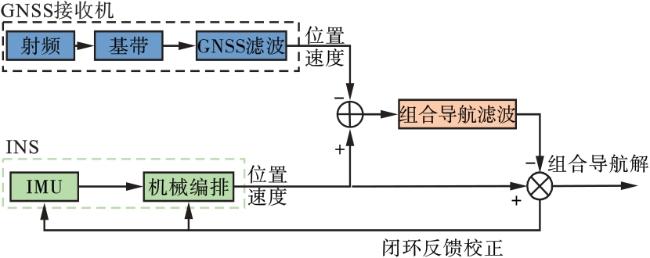
全球导航卫星系统因其精度高、覆盖全球和全天候运行的优点得到广泛应用［1-2］，然而其存在信号易受干扰或遮挡的缺点［3-4］。惯性导航系统运行不依赖于外部信息能够提供连续的三维运动状态参数信息，因而在航天、航空、船舶及陆地车辆等运动载体定位测姿中得到广泛应用，但其存在误差随时间累积的缺点。将两者结合能够有效地克服单一导航系统的不足，进而提高导航定位的精度、连续性和可靠性等性能［5］。GNSS/INS组合方式主要有松组合（loosely coupled，LC）和紧组合（tightly coupled，TC）两种。松组合方式是将GNSS和INS各自输出的导航结果输入到组合导航滤波器中，估计惯性元件误差和INS导航误差，这种组合模式结构简单。紧组合方式是利用滤波器融合GNSS和INS的原始观测值来修正INS误差，这种组合方式结构复杂，但在卫星数不足的情况下仍可进行导航定位。
在GNSS/INS组合导航中可以采用不同的非线性滤波器进行数据融合，例如粒子滤波（particle filter，PF）和无迹卡尔曼滤波（unscented Kalman filter，UKF），其中扩展卡尔曼滤波（extended Kalman filter，EKF）的应用最为广泛。但是，针对复杂的应用环境，例如在高动态和强干扰的情况下，由于滤波的后验性和系统的不确定性，卡尔曼滤波器将出现滤波发散的问题，特别是在GNSS信号受到遮挡等干扰出现失效的情况下，惯性导航的误差将迅速累积，从而导致导航精度下降［6］。近年来，以神经网络为代表的人工智能发展迅速，因其对非线性问题具有较好的处理能力和逼近拟合函数等优点，在卫星导航领域发挥着重要作用。文献［7］针对GPS信号不可用时，捷联惯性导航系统（strapdown inertial navigation system，SINS）和GPS组合导航系统定位精度产生较大退化的问题，研究了遗传算法优化的径向基函数神经网络（radial basis function neural network，RBFNN）辅助组合导航系统定位的方法。文献［8］研究了一种新的混合融合算法提供辅助组合导航系统的伪位置信息。结合卡尔曼滤波（Kalman filter，KF）和改进的多层感知器（multi-layer perception，MLP）网络，在GPS信号不可用的情况下对GPS位置进行预测和估计。为了抑制惯导系统误差发散，文献［9-10］提出了自适应量子粒子群算法和人工蜂群算法改进的径向基神经网络与自适应卡尔曼滤波算法。与单一SINS系统相比，上述神经网络在卫星信号中断期间能改善导航系统的定位精度。文献［11］研究了一种基于反向传播神经网络（back propagation neural network，BPNN）的融合算法，建立了INS速度、惯性测量单元（inertial measurement unit，IMU）输出和GPS中断持续时间与GPS位置增量之间的关系模型。为解决BPNN无法处理时间序列数据的问题，文献［12］研究了一种基于循环神经网络（recurrent neural network，RNN）的GNSS/INS组合导航方法。针对MLP基于INS误差和INS输出的建模，忽略了对过去车辆动态信息的依赖，导致导航精度差的问题，文献［13-14］研究了基于长短期记忆（long short-term memory，LSTM）网络的惯性导航系统辅助算法。文献［15］研究了一种基于门控循环单元（gated recurrent unit，GRU）和交互式多模型自适应鲁棒容积卡尔曼滤波（interacting multiple model-adaptive robust cubature Kalman fillter，IMM-ARCKF）的混合算法。考虑到GRU预测的误差累积，文献［16］研究了一种基于门控循环单元和自适应卡尔曼滤波器（adaptive extended Kalman fillter，AKF）的混合算法，引入AKF作为辅助方法来提高导航性能。尽管LSTM和GRU在处理一些问题（特别是序列预测问题）时表现出较好的能力，但它们仍然存在一些如计算复杂度高、时效性差且需要大量的训练数据才能进行有效训练等缺点。
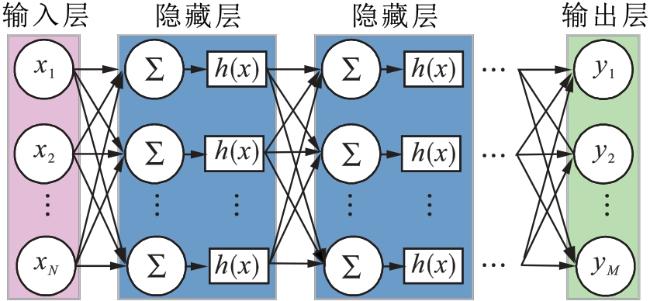
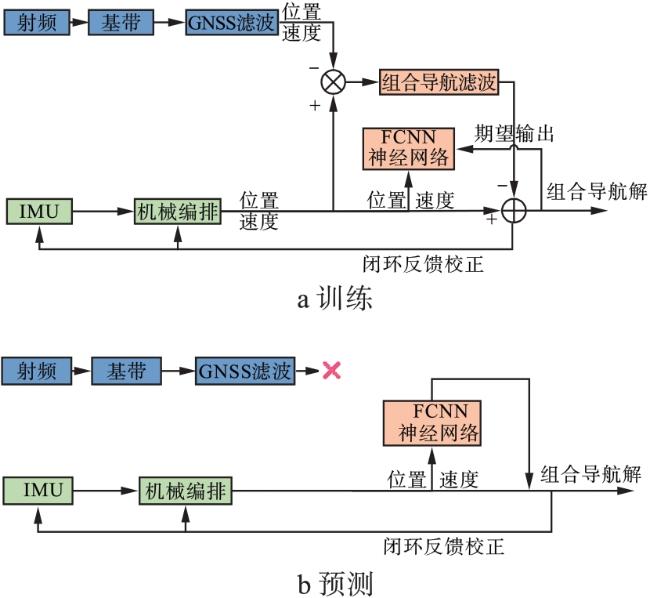
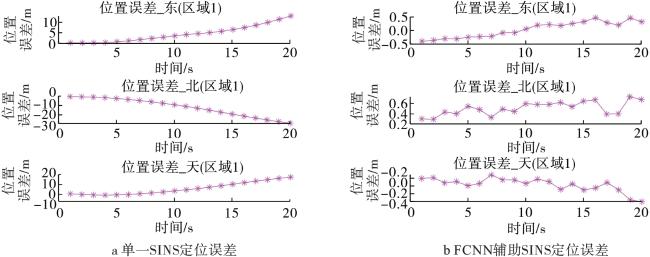
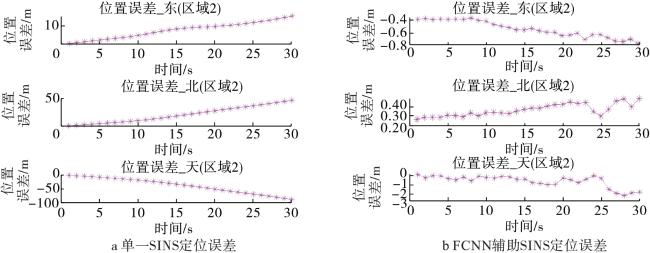
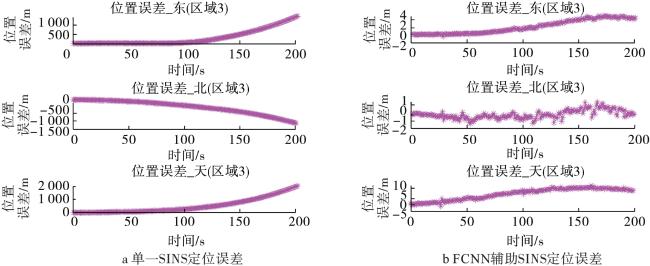
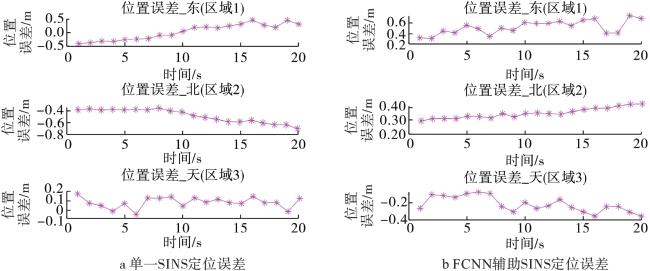
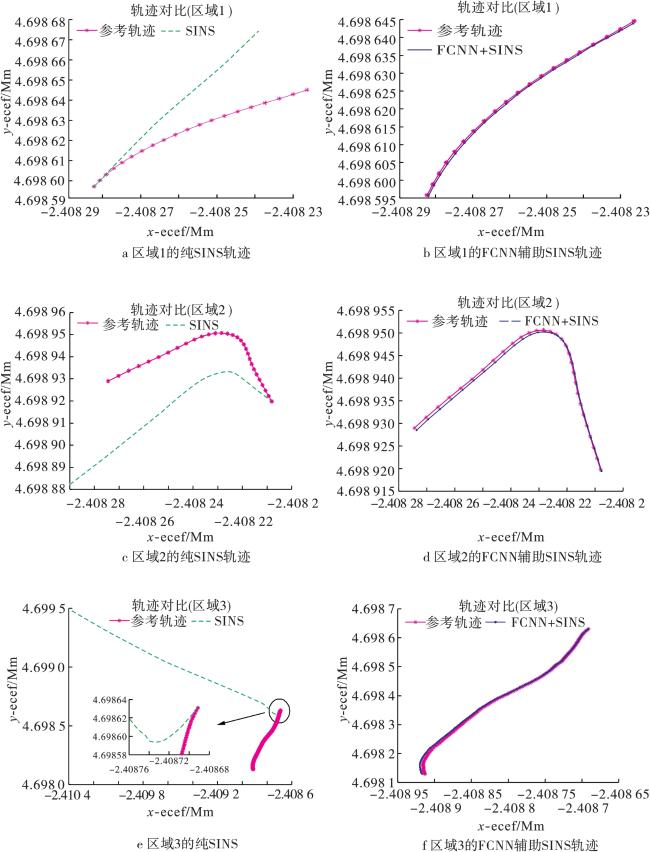
综上所述，针对复杂的应用环境，特别是在GNSS信号受到遮挡等干扰导致失效时，惯性导航的误差将迅速累积，导致导航精度下降，本文提出了一种基于全连接神经网络的GNSS/INS组合导航定位方法。在GNSS信号接收正常时，利用INS解算的位置速度信息和组合导航解对FCNN模型进行训练；在GNSS信号中断后，利用训练好的FCNN模型预测导航位置与速度信息。最后，利用实测车载数据进行实验验证。

1 GNSS/INS松组合定位模型

GNSS/INS松组合利用组合导航滤波器对GNSS输出的位置速度和INS输出的导航解进行融合，以实现组合导航系统导航参数的解算，松组合结构如图1所示。
图1 GNSS/INS松组合结构图
本文中GNSS/INS松组合定位使用传统的15维状态向量，可表示为
x = φ δ v n δ p b g b a T
式中： φ为姿态误差向量； δ v n为惯导速度误差向量； δ p为惯导位置误差向量； b g为三轴陀螺零偏向量； b a为三轴加速度计零偏向量。
离散形式的线性化状态空间模型如式（2）、（3）所示。
x k = Φ k ,   k - 1 x k - 1 + w k - 1
z k = H k x k + v k
式中： x k和 x k - 1分别为 k、 k - 1时刻的状态向量； Φ k ,   k - 1为 k - 1时刻到 k时刻的状态转移矩阵； z k为 k时刻观测向量； H k为 m × n阶观测矩阵； w k - 1和 v k分别为过程噪声和量测噪声。对应的协方差矩阵分别为 Q k和 R k。采用卡尔曼滤波器的组合导航状态最优估计表示为
x ^ k / k - 1 = Φ k / k - 1 x ^ k - 1 P k / k - 1 = Q k - 1 + Φ k / k - 1 P k - 1 Φ k / k - 1 T K k = P k / k - 1 H k T ( H k P k / k - 1 H k T + R k ) - 1 x ^ k = x ^ k / k - 1 + K k z k - H k x ^ k / k - 1 P k = I - K k H k P k / k - 1
式中： P k表示状态的协方差矩阵； K k表示卡尔曼增益矩阵。

2 基于神经网络的组合导航模型

2.1 全连接神经网络模型

全连接神经网络模型包括输入层、隐藏层及输出层3个部分，其基本结构如图2所示，网络的每一层都仅与前一层和后一层有连接，降低了结构的复杂性。同时，FCNN每层网络所有的神经元都与前一层和后一层的所有神经元相连，这种神经元之间的高度连接性使FCNN模型具有较强的学习和适应能力。
图2 全连接神经网络模型结构图
假设全连接神经网络的层数为 L，每层包含 N ( l )个神经元，其中， l表示层的索引。各部分在网络模型中的作用如下：
（1）输入层：输入层接收外部输入数据。假设输入层为第 0层，输入向量为 x，则输入层包含 N ( 0 )个神经元，输入向量 x的长度等于输入层神经元的数量，即 N ( 0 )。
（2）隐藏层：全连接神经网络可以包含1个或多个隐藏层。假设有 L - 1个隐藏层，其中第 l个隐藏层包含 N ( l )个神经元。每个隐藏层的神经元都与前一层的所有神经元相连。
（3）输出层：输出层接收最后一个隐藏层的输出，并产生最终的输出结果。假设输出向量为 y，则输出层包含 N (   L   )个神经元。输出向量 y的长度等于输出层神经元的数量，即 N (   L   )。
在全连接神经网络中，每个神经元都具有一个权重向量 w (   l   )和一个偏置 b (   l   )。对于每个神经元，其输入是前一层的所有神经元的输出。所以，每个神经元的输出可以表示为
a j (   l   ) = h ( ∑ i = 1 N (   l - 1   ) w i j (   l   ) ⋅ a i (   l - 1   ) + b j (   l   ) )
式中： a j (   l   )为第 l层中第 j个神经元的输出； w i j (   l   )为连接第 l - 1层第 i个神经元到第 l层第 j个神经元的权重； a i (   l - 1   )为第 l - 1层中第 i个神经元的输出； b j (   l   )为第 l层中第 j个神经元的偏置； h ⋅为激活函数。全连接神经网络根据式（5）计算每个神经元的输出，从输入层一直传递到输出层来进行预测或分类任务。

2.2 基于FCNN模型的组合导航模型

基于FCNN的组合导航系统模型包括训练和预测两个部分，如图3所示。在GNSS信号正常时，将GNSS和INS输出的位置速度差输入到组合导航滤波器中进行数据融合，输出INS最优估计误差反馈至INS进行校正，并利用INS解算的位置和速度信息作为网络输入，组合导航解作为网络期望输出，对网络进行训练处理；当GNSS信号失效时，利用完成训练的神经网络对INS输出的位置速度进行处理，并输出预测的组合导航位置解。
图3 基于FCNN的GNSS/INS组合导航系统模型
本文研究的FCNN模型共由5层组成，每一层承担着不同的数据处理和特征学习功能。第一层作为输入层，其神经元数量与输入数据的维度相匹配。

3 实验验证与结果分析

3.1 实验数据和条件设置

本文选用网络公开的车载数据进行算法验证分析［17］。该数据采集使用的GNSS接收机为TrimbleR10，IMU为SPAN-CPT，基线长度为1.5 km。其中，GNSS接收机采样频率为1 Hz，INS采样频率为100 Hz，采集时长为2 400 s。其中IMU相关性能指标如表1所示。
表1 IMU性能指标
相关参数 陀螺仪 加速度计
零偏 2 deg/h 2 mg
零偏不稳定性 0.05 deg/h 7.5 mg
随机游走 0.012 deg/sqrt（h） 119 μg/sqrt（Hz）
选取其中12 00 s的动态数据作为实验数据。为了模拟卫星信号失效的情况，在实验中人为设定3个卫星信号中断区域，GNSS信号中断时间设置情况如表2所示。这些数据为GNSS信号中断的系统测试集，用于验证本文所提算法对组合定位误差的抑制效果。其余时间的数据作为系统的训练集，用来训练优化FCNN神经网络模型中的参数。
表2 GNSS信号中断的时间设置 (s)
区域 区域特征 中断时间段 中断时长
1 右转弯 201~220 20
2 左转弯 316~345 30
3 直线 469~668 200
在使用FCNN模型进行训练时，通常会定义一个损失函数来衡量模型预测结果与真实标签之间的差异，然后通过调整模型参数，使得这个损失函数的值最小化，即尽可能减小预测误差。在本文中，所有神经网络都以相同的模式运行，FCNN模型部分参数设置如表3所示。
表3 FCNN模型部分参数设置
参数 值
输入特征数量 6
输出特征数量 3
隐藏神经元数量 30
迭代次数 1000
学习率 0.01

3.2 实验结果分析

利用Novatel Inertial Explorer8.6软件在平滑实时动态载波相位差分技术（real-time kinematic，RTK）/INS 紧组合模式下得到的解作为高精度参考真值。分析GNSS信号失锁情况下，不同区域FCNN神经网络辅助SINS和单一SINS的定位误差。表4和表5分别列出了各中断时间段内，SINS和FCNN辅助SINS在东（E）、北（N）、天（U）3个方向上的位置及速度均方根（root mean square，RMS）误差。
表4 各中断时间段内位置均方根误差 (m)
算法 方向 区域1 区域2 区域3
FCNN+SINS E 0.276 0.557 4.500
N 0.531 0.365 2.686
U 0.181 0.889 3.192
SINS E 5.761 8.536 550
N 15.332 24.947 46.285
U 487.78 560.49 731.72
表5 各中断时间段内速度均方根误差 (m·s-1)
算法 方向 区域1 区域2 区域3
FCNN+SINS E 0.104 0.037 0.187
N 0.128 0.028 0.342
U 0.127 0.386 0.687
SINS E 0.788 0.542 10.400
N 1.634 1.625 7.751
U 1.200 3.071 13.262
由图4 — 6及表4可知，部分GNSS信号中断情况下，不同区域单一SINS定位结果出现发散。GNSS信号中断20 s时，SINS东、北向误差分别超过10、20 m，而FCNN辅助SINS水平方向仍能保持较高定位精度。对于区域3，GNSS中断120 s时，单一SINS东、北向最大误差分别为158.8、449.4 m，FCNN辅助SINS东、北向最大误差分别提升至2.5、0.3 m。结合表5发现，单一SINS的速度均方根误差整体上高于FCNN辅助SINS算法。在区域3中，U向的速度均方根误差最高，达到13. 262 m/s，这表明GNSS信号中断情况下，单一SINS测速稳定性较差，而FCNN辅助SINS能够显著降低测速误差，提高其准确性和稳定性。
图4 区域1单一SINS定位误差与FCNN辅助SINS定位误差
图5 区域2 单一SINS定位误差与FCNN辅助SINS定位误差
图6 区域3单一SINS定位误差与FCNN辅助SINS定位误差
由图7可以看出，在相同中断时间内，相较区域3的直线运动，区域1和区域2的误差更大，但相比单一SINS的指数级发散，FCNN神经网络辅助SINS的定位误差仍在可接受的范围内，短时间内可满足用户定位性能要求。
图7 同一中断时长（20 S）下不同区域下单一SINS与FCNN定位误差对比
不同区域SINS和FCNN辅助SINS与参考真值的东北方向二维位置分别如图8所示。从二维位置可看出，在GNSS中断后的20 s后，SINS的位置信息出现了发散现象，其终点位置与参考真值终点位置有很大的偏差。FCNN辅助SINS的轨迹信息同实际路线具有很好的拟合和一致性，可以看到GNSS信号中断后FCNN网络模型能够较为准确地预测出用户位置，验证了基于FCNN模型的组合导航算法的有效性。
图8 不同区域下FCNN辅助SINS和单一SINS定位结果对比

4 结论

针对GNSS信号中断或失效导致GNSS/INS组合导航定位误差增大的问题，本文提出了一种基于FCNN的GNSS/INS组合导航定位方法。该方法分为训练和预测两个模块，利用GNSS信号正常区域的INS定位解与组合系统输出解训练FCNN模型参数；在GNSS信号中断区域，根据已经训练好的FCNN模型预测组合导航定位解。通过实测数据验证，所提算法能够有效地抑制GNSS中断时纯SINS误差发散的情况，提高了GNSS信号中断或失效时组合导航系统的定位精度和连续性，本文为复杂环境下组合导航定位精度与可靠性的提升技术参考。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
1
Guo J， Li X X， Li Z H，et al.Multi-GNSS precise point positioning for precision agriculture［J］.Precision Agriculture，2018，19（5）：895-911.

2
Wu Q， Sun M F， Zhou C J，et al.Precise point positioning using dual-frequency GNSS observations on smartphone［J］.Sensors，2019，19（9）：2189.

3
王尔申，朱骏，徐嵩，等.基于无迹卡尔曼滤波的BDS/INS组合定位方法［J］.沈阳航空航天大学学报，2023，40（4）：19-24.

4
王尔申，孙彩苗，黄煜峰，等.改进粒子群优化的卫星导航选星算法［J］.北京航空航天大学学报，2021，47（1）：1-6.

5
Gonzalez R， Dabove P.Performance assessment of an ultra low-cost inertial measurement unit for ground vehicle navigation［J］.Sensors，2019，19（18）：3865.

6
高为广，陈谷仓.结合自适应滤波和神经网络的GNSS/INS抗差组合导航算法［J］.武汉大学学报（信息科学版），2014，39（11）：1323-1328.

7
徐晓苏，周峰，张涛，等.遗传算法优化的神经网络在SINS/GPS中的应用［J］.中国惯性技术学报，2015，23（3）：322-327.

8
Yao Y Q， Xu X S， Zhu C C，et al.A hybrid fusion algorithm for GPS/INS integration during GPS outa-ges［J］.Measurement，2017，103（1）：42-51.

9
陈光武，李文元，于月，等.基于改进径向基神经网络的MEMS惯导系统误差抑制方法［J］.中国惯性技术学报，2019，27（1）：15-22，94.

10
陈光武，程鉴皓，杨菊花，等.基于改进神经网络增强自适应UKF的组合导航系统［J］.电子与信息学报，2019，41（7）：1766-1773.

11
Wang G C， Xu X S， Yao Y Q，et al.A novel BPNN-based method to overcome the GPS outa-ges for INS/GPS system［J］.IEEE Access，2019（7）：82134-82143.

12
Dai H F， Bian H W， Wang R Y，et al.An INS/GNSS integrated navigation in GNSS denied environment using recurrent neural network［J］.Defence Technology，2020，16（2）：334-340.

13
Fang W， Jiang J G， Lu S Q，et al.A LSTM algorithm estimating pseudo measurements for aiding INS during GNSS signal outages［J］.Remote Sen-sing，2020，12（2）：256.

14
张跃发.神经网络辅助的GNSS/INS车载组合导航算法研究［D］.西安：长安大学，2023.

15
Li D A， Wu Y Q， Zhao J M.Novel hybrid algorithm of improved CKF and GRU for GPS/INS［J］.IEEE Access，2020（8）：202836-202847.

16
Tang Y N， Jiang J G， Liu J H，et al.A GRU and AKF-based hybrid algorithm for improving INS/GNSS navigation accuracy during GNSS outage［J］.Remote Sensing，2022，14（3）：752-757.

17
Chen K， Chang G B， Chen C.GINav：a MATLAB-based software for the data processing and analysis of a GNSS/INS integrated navigation system［J］.GPS Solutions，2021，25（3）：108.

Options
文章导航

/

〈 〉

网站版权 © 《沈阳航空航天大学学报》编辑部
地址：沈阳市沈北新区道义南大街37号沈阳航空航天大学学报编辑部　
邮编：110136
电话：024-89723779　
传真：024-89723779　
E-mail：shxbok@163.com
本系统由北京玛格泰克科技发展有限公司设计开发