基于EDAS的高端装备制造业协同创新伙伴选择

施慧斌; 陈园园; 何悦丽; 张慧

doi:10.3969/j.issn.2095-1248.2024.03.011

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 3: 85 - 96

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.03.011

管理科学与工程

基于EDAS的高端装备制造业协同创新伙伴选择

施慧斌 ^,^a ,
陈园园 ^a ,
何悦丽 ^a ,
张慧 ^b

展开

^a. 沈阳工业大学，管理学院，沈阳 110870
^b. 沈阳工业大学，理学院，沈阳 110870

施慧斌(1982-),男,辽宁沈阳人,副教授,博士,主要研究方向:创新管理、项目管理,E-mail:hhbbs@163.com。

收稿日期: 2024-03-12

网络出版日期: 2024-08-30

基金资助

辽宁省社会科学规划基金(L19BGL028)

收起

Selection of collaborative innovation partners in the high-end equipment manufacturing industry based on EDAS

Huibin SHI ^,^a ,
Yuanyuan CHEN ^a ,
Yueli HE ^a ,
Hui ZHANG ^b

Expand

^a. College of Management, Shenyang University of Technology，Shenyang 110870，China
^b. College of Science, Shenyang University of Technology，Shenyang 110870，China

Received date: 2024-03-12

Online published: 2024-08-30

Fold

摘要

伴随市场环境的复杂多变，高端装备制造业必须通过协同创新来增强技术实力及提高创新成效，其中伙伴选择是其实现创新的关键一步。首先，分析总结伙伴选择评价指标相关文献，并结合高端装备制造业协同创新发展需求，从互补性、兼容性、创新资源、创新能力、创新环境、声誉与信任及技术水平这7个维度，建立了高端装备制造业协同创新伙伴选择指标体系；然后，考虑到高端装备制造业的复杂性及专家评价的模糊性，在概率犹豫模糊环境下，构建基于可能度的平均解距离法（evaluation based on distance from average solution，EDAS）群决策评价模型，并将其应用到该指标体系下的协同创新伙伴选择中；最后，通过一个算例，对该研究方法加以验证，为高端装备制造业进行协同创新伙伴选择提供一定的参考。

关键词： 高端装备制造业; 协同创新; 伙伴选择; 平均解距离法; 群决策

本文引用格式

施慧斌 , 陈园园 , 何悦丽 , 张慧 . 基于EDAS的高端装备制造业协同创新伙伴选择[J]. 沈阳航空航天大学学报, 2024 , 41(3) : 85 -96 . DOI: 10.3969/j.issn.2095-1248.2024.03.011

Abstract

In the complex and changing market environment， high-end equipment manufacturing industry must enhance technical strength and improve innovation effectiveness through collaborative innovation， of which partner selection is a key step to achieve innovation. Firstly， by analyzing and summarizing relevant literatures on partner selection evaluation indicators， and combining with the colla-borative innovation development needs of high-end equipment manufacturing industry，the collaborative innovation partner selection index system of high-end equipment manufacturing industry was estab-lished from seven dimensions： complementarity， compatibility， innovation resources， innovation ability，innovation environment， reputation and trust as well as technical level. Then，considering the complexity of the high-end equipment manufacturing industry and evaluation fuzziness，a group decision-making model of EDAS was constructed based on possibility under the probabilistic hesitancy fuzzy environment，and applied it to the collaborative innovation partner selection under indicator system. Finally，a numerical example was used to verify the research method，which provides a certain reference for the collaborative innovation partner selection of high-end equipment manufacturing industry.

Key words： high-end equipment manufacturing industry; collaborative innovation; partner selection; evaluation based on distance from average solution（EDAS）; group decision-making

目前我国正在推进新型工业化，加快建设制造强国，这在一定程度上推动了装备制造业的发展。然而随着其在工业领域的快速发展，为了提升区域产业的核心竞争力，必须重视高端装备制造业的发展。高端装备制造业又被称为先进制造业，是指生产制造高技术、高附加值的先进工业设施设备的行业，其具有较高市场竞争力，为带动我国制造业发展起到引领作用^［1］。然而，技术水平、创新资源等问题制约其发展进程与效果，且该领域参与方较多、涉及面较广，技术创新难度较大，为了持续高效发展，必须对其进行协同创新。装备制造业协同创新是以企业为主要创新主体，联合高校、研究所等重要知识伙伴，在政府辅助下，改变固有创新范式，进行多方协作^［2］。在协同创新背景下，伙伴选择对高端装备制造业至关重要，候选伙伴质量将决定协同创新的最终成果。所以，本文对高端装备制造业协同创新伙伴选择加以探讨，对于完善高端装备制造业创新体系、提高高端装备制造领域技术水平及建设制造强国有着重要意义。

目前关于协同创新伙伴选择的相关研究成果较多，研究内容主要集中于伙伴选择指标体系及评价方法两大方面。伙伴选择指标体系主要考虑以下几个因素：互补性与兼容性^［3］、创新资源与合作情况^［4］、信任度与研发能力^［5］、技术方案以及创新效果等^［6］；伙伴选择方法方面有偏好顺序结构评估（preference ranking organization method for enrichment evaluations，PROMETHEE）多属性决策法、结合最优最劣法（best-worst method，BWM）的折衷排序VIKOR法、基于熵权的优劣解距离法（technique for order preference by similarity to an ideal solution，TOPSIS）等。

综上，伙伴选择相关研究理论较为丰富，但针对高端装备制造业协同创新伙伴选择的研究相对较少，评价体系不完善且评价方法较为单一。因此，为了帮助高端装备制造业开展协同创新伙伴选择，本文通过建立更加全面和科学的伙伴选择指标体系，并构建基于可能度的EDAS伙伴选择群决策模型，为高端装备制造业协同创新伙伴选择提供一定的参考价值。

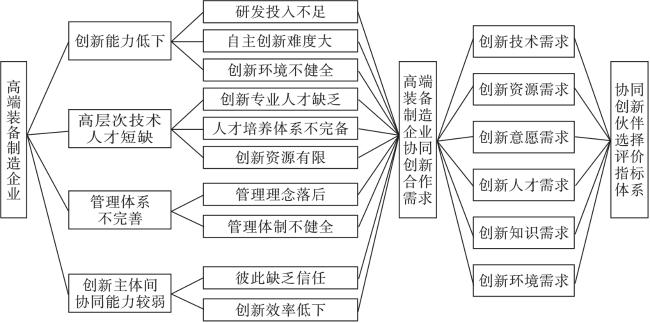
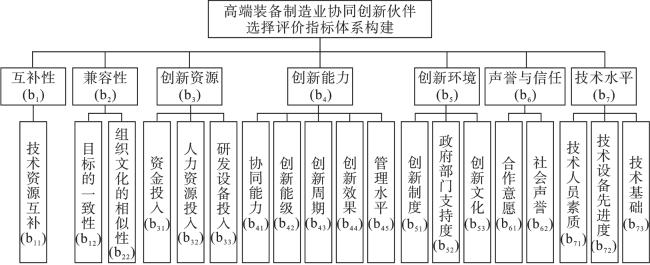
1 高端装备制造业协同创新伙伴选择评价指标构建

1.1 伙伴选择评价指标体系建立过程

本文在指标体系选择方面，结合了国内外大量文献，部分学者在创新伙伴选择时考虑的指标因素如表1所示。

表1 国内外创新伙伴选择评价指标

指标来源	评价指标
Shevtshenko 等^［10］	合作成本、合作风险和创新效率
Santos 等^［11］	经济（财务状况及信誉、运营状况）、社会（声誉、知识相关性、可用资源）及环境（政府支持度）
Arsanti 等^［12］	互补性（技术与资源）、兼容性（目标及文化一致）和信任性
Chowdhury 等^［13］	价值提供、技术复杂性及组织间兼容性
Li等^［14］	主体间的利益分配模式、技术创新水平、组织结构、合作意愿与兼容性
刘澜等^［15］	管理水平、经济情况、人力资源、技术水平、信誉度及兼容性
李柏洲等^［16］	创新能力、兼容性、信任度与合作意愿
李柏洲等^［17］	合作水平、聚合资源能力及合作聚合度
李翠等^［18］	互补性、兼容性、企业规模、技术水平、财务状况和企业发展情况
孟贤等^［19］	合作成本、服务水平、风险共担能力及信息共享能力
刘嘉等^［20］	生产能力、质量评估、业务能力、合作互补性及环境影响
李红艳等^［21］	人力资源条件、财力资源条件、设备资源条件、协同意愿、协同沟通能力及协同创新产出能力
黄哲等^［22］	基本条件、运营状态、企业文化、资源互补性、契约精神、信任度和技术实力

通过对以上大量文献的总结可知，在协同创新伙伴选择过程中，大多数学者将互补性、兼容性、信誉度及技术水平等作为挑选候选伙伴的主要考察因素，部分学者也将社会环境要素考虑在内。在现有研究的基础上，考虑高端装备制造业创新发展问题及实际创新合作需求的指标体系建立过程如图1所示，对协同创新伙伴的选择增加一些新的内容，例如在创新资源方面考虑研发设备投入、增添创新周期与创新效果要素及考虑当下创新环境的重要影响等。

显示原图|下载原图ZIP|生成PPT

图1 创新伙伴选择评价指标体系建立过程

1.2 评价指标体系的确定

基于以上分析过程，结合高端装备制造业协同创新的现实需求，本文将从互补性、兼容性、创新资源、创新能力、创新环境、声誉与信任及技术水平这7个维度建立协同创新伙伴选择指标体系，如图2所示。

显示原图|下载原图ZIP|生成PPT

图2 高端装备制造业协同创新伙伴选择评价指标体系

2 高端装备制造业协同创新伙伴选择评价模型构建

本文考虑到高端装备制造业协同创新伙伴选择的必要性、复杂性及不确定性，同时兼顾决策者评价偏好，提出建立一种基于可能度的概率犹豫模糊EDAS伙伴选择群决策模型。其中通过社会网络信任关系求解决策者权重，指标权重通过主客观结合得出。相比于TOPSIS、VIKOR，EDAS评价方法^［23］将评价标准由极端的优劣思想解转化为更具有实际意义的平均解，可以解决某些有矛盾性质的指标，而且计算过程较为稳定简单，可以更好地帮助高端装备制造企业在众多的协同创新伙伴中挑选出最为合适的合作伙伴，有助于提高高端装备制造业协同创新水平与效率。

2.1 评价矩阵

2.1.1 问题描述

假设在高端装备制造业协同创新环境下，领先创新主体企业给出创新任务后，将会依据创新项目特征及技术需求，挑选出i个待选合作对象，记为X_i （i=1，2，…，m）。诚邀k位决策专家参与决策，专家表示为E_k （k=1，2，…，s），专家权重为

λ k = (λ 1, λ 2, …, λ s)

。b_j （j=1，2，…，n）为每个待选伙伴的评价指标，指标权重为w_j =（w ₁，w ₂，…，w_n ）。为了方便决策专家更好地表达内心想法，让其使用犹豫模糊集H_ij =（h_ij ）表示对候选伙伴X_i 在指标b_j 方面的决策意见。然后对决策者意见进行转化，得出协同创新伙伴X_i 在指标b_j 方面的综合决策意见，用概率犹豫模糊集H _ij =（h_ij |p_ij ）来表示，所有决策意见所形成的评价矩阵为 Q =（H_ij ） _m _× _n。

2.1.2 评价矩阵聚合

本文将利用PHFOWA算子对每位决策专家给出的评价信息进行聚合，假设

h i p = {γ i l (p i l) | l = 1,2, …, | h i p |} (i = 1,2, …, n)

是一个n维概率犹豫模糊集，

h i (i = 1,2, …, n)

分别是其模糊元，

h i p

的权重为

w = (w 1, w 2, …, w n)

，

w i ∈ 0,1

，

i = 1,2, …, n

，且

∑ i = 1 n w i = 1

。则^［24］

P H F O W A h 1 p, h 2 p, …, h n p

= ⊕ i = 1 n w i h i p

= ⋃ γ 1 l ∈ h 1, γ 2 l ∈ h 2, …, γ n l ∈ h n 1 - ∏ i = 1 n 1 - γ i l w i ∑ i = 1 h i p p i l ¯

（1）

其中

∑ i = 1 | h i p | p i l = ∑ i = 1 | h i p | p i l / ∑ l = 1 k ∑ i = 1 | h i p | p i l, k = 1, …, l

。

2.2 权重计算

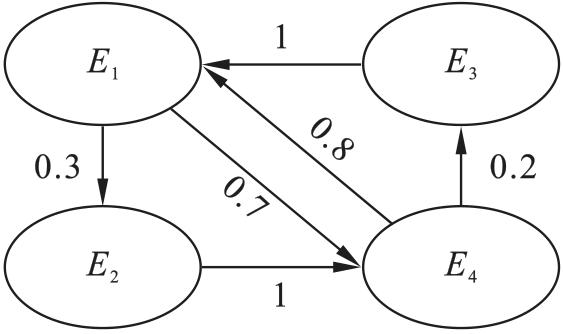
2.2.1 基于社会网络信任关系的决策专家权重计算

社会网络信任关系可以体现决策专家的社会关系，主要包括以下三大概念：

（1）参与者是参与评价的决策者，代表节点；

（2）参与者之间的信任关系表达节点之间的连接；

（3）参与者属性是为了说明参与者的特征。

通过一个简单例子展示社会关系矩阵与社会关系图。

（1）社会关系矩阵

常以邻接矩阵 A 的形式出现，表达决策者两两之间的社会关系。例如

A = E k E 1 E 2 E 3 E 4 E 1 0 0.3 0 0.7 E 2 0001 E 3 1000 E 4 0.8 0 0.2 0

（2）社会网络关系图如图3所示

显示原图|下载原图ZIP|生成PPT

图3 社会网络关系

邻接矩阵 A 中的结果表示决策者对对方的信任度，信任度介于［0，1］之间，数值越大表明信任强度越大，反之则越小，决策者的网络节点入度指数可由邻接矩阵得出。决策者k（k=1，2，3，4）的入度指数为

ϑ k = 1 s - 1 ∑ k = 1, j ≠ k s a j k

（2）

其中，s=4，a_jk 为邻接矩阵 A 中的元素。

当

ϑ k

值越大，表明决策者的影响力就越大，其权重就更大，决策专家权重为

λ k = ϑ k ∑ k = 1 s ϑ k

（3）

2.2.2 评价指标权重计算

（1）基于离差最大化法求解指标客观权重^［25］

假设H=（h|p）是一组概率犹豫模糊集，则其得分函数为

S = (∑ i = 1, γ ∈ h | h i p | γ i p i) / (∑ i = 1 | h i p | p i)

（4）

依据评价指标得分函数确定指标权重求解模型

m a x f w = ∑ i = 1 m ∑ g = 1 m ∑ j = 1 n | S i j - S g j | w j'

s . t . ∑ j = 1 n (w j') 2 = 1,0 ≤ w j' ≤ 1

（5）

通过拉格朗日求解可得

w j' = ∑ i = 1 m ∑ g = 1 m | S i j - S g j | ∑ j = 1 n (∑ i = 1 m ∑ g = 1 m | S i j - S g j |)

（6）

（2）基于BWM法求解指标主观权重

BWM法^［26］是选出最好的与最差的指标，将其余指标与两者分别进行对比，然后通过计算极大值与极小值获得各个指标的权重，主要步骤如下：

首先，通过求解出的客观权重来确定评价指标中最好与最坏指标；

然后，确定指标间的对比关系，通过标度1~9确定其余指标相比于参照指标的对比关系，最重要指标与其余指标的对比向量

A B = (a B 1, a B 2, …, a B n) T

，

a B j = w B w j

代表最重要指标和第j个指标的比值，

a B B = 1

。最差指标与其余指标的对比向量为

A w = (a 1 w, a 2 w, …, a m w) T

，

a j w = w j w w

代表第j个指标和最差指标的比值，

a w w = 1

；

其次，建立规划模型，确定最优结果；

m i n m a x | w B - a B j w j |

和

| w j - a j w w w |

s . t . ∑ j = 1 n w j = 1, w j ≥ 0

（7）

将上述模型转化为线性规划模型

m i n ς

s . t . w B - a B j w j ≤ ς, j = 1,2, …, n w j - a j w w w ≤ ς, j = 1,2, …, n ∑ j = 1 n w j = 1, w j ≥ 0

（8）

采用一致性比率CR判断指标间的可靠性程度，对比其一致性水平。其中CR值越小，则说明指标的一致性就越好，一般来说，

C R ≤ 0.1

表明指标的一致性较优，

C R ≤ 0.25

时表明评价结果一致，公式如式（9）所示。

C R = ς C I

（9）

针对不同的

a B W ∈ {1,2, …, 9}

，一致性指数的结果如表2所示。

表2 1~9标度所对应的一致性指数

$a B W$	1	2	3	4	5	6	7	8	9
一致性指数	0.00	0.44	1.00	1.63	2.30	3.00	3.73	4.47	5.23

（3）指标综合权重的确定

本文基于以上两种方法求解评价指标权重，其组合权重如式（10）所示

w b j = φ w j' + ϕ w j

（10）

式中：

φ

与

ϕ

是平衡系数，本文取

φ = ϕ = 0.5

。

2.3 基于可能度矩阵的概率犹豫模糊EDAS决策方法

EDAS在多个领域都有应用，比如可持续发展管理、供应商选择等决策问题。本文将其引入到概率犹豫模糊环境下，拓展其应用深度。

2.3.1 可能度矩阵

Song等^［27］定义了概率犹豫模糊可能度。

（1）假设

h 1 p

和

h 2 p

为两个概率犹豫模糊元（probabilistic hesitant fuzzy elements，PHFE），则

h 1 p ≥ h 2 p

的可能度公式为

p h 1 p ≥ h 2 p = m a x 0, α + h 1 - α - h 2 - m a x 0, α - h 1 - α + h 2 I h 1 + I h 2

（11）

其中：

I h i = ς + h i p + h i - ς - h i p - h i,

ς + h i p + h i = m a x ς τ h i p τ h i τ = 1,2, …, l,

ς - h i p - h i = m i n ς τ h i p τ h i τ = 1,2, …, l,

α ± h i = ς ± h i p ± h i, i = 1,2

。

（2）

h i p

优于其余PHFE的整体优势度为

p i' = ∑ k = 1, k ≠ i n p' h i p ≥ h k p

（12）

2.3.2 EDAS决策排序

EDAS决策步骤如下^［28］：

（1）整理专家初始评价信息，得到每个决策者的

Q i

，确定决策专家权重、评价指标权重及综合评价矩阵 Q =［H_ij ］ _m _× _n。

（2）基于可能度矩阵确定各评价指标下的平均解AV如式（13）所示

A V = [A V j] 1 × n

（13）

其中

A V j = {i = 1 n ⊕ h i p m 1 m, m 为排 序中 间值 个数}

。

（3）依据不同的属性类别，分别计算出其正向距离矩阵PDA及负向距离矩阵（NDA）为

P D A = (P D A i j) m × n

；

N D A = (N D A i j) m × n

P D A i j

= m a x 0, d P i j, P - d A V j, P d A V j, P, i ∈ T 1 m a x 0, d A V j, P - d P i j, P d A V j, P, i ∈ T 2

（14）

N D A i j

= m a x 0, d A V j, P - d P i j, P d A V j, P, i ∈ T 1 m a x 0, d P i j, P - d A V j, P d A V j, P, i ∈ T 2

（15）

式中：P取概率犹豫模糊最小元素；

T 1

与

T 2

依次为效益型指标、成本型指标；假设h ₁（P）、h ₂（P）为两个概率犹豫模糊元，则

d h 1, h 2 = 12 ∑ l = 1 λ γ 1 l p 1 l - γ 2 l p 2 l + γ 1 l - γ 2 l p 1 l p 2 l

。

（4）计算各候选协同创新伙伴的加权PDA总和与加权NDA总和

S P i = ∑ j = 1 n w j P D A i j

（16）

S N i = ∑ j = 1 n w j N D A i j

（17）

（5）计算待选伙伴的综合评价值

A S i

A S i = 12 S P i m a x i S P i + 1 - S N i m a x i S N i

（18）

（6）依据

A S i

结果，对协同创新候选伙伴

X i (i = 1,2, …, m)

进行排序。

3 算例分析

3.1 算例应用

某企业为了攻克高速精密数控机床关键功能部件技术难题，需要具有相关数控研发能力的协同创新合作伙伴一起参与研发。通过专家介绍及初步的筛选，选出4位符合条件的创新伙伴，依次记为X ₁，X ₂，X ₃，X ₄。邀请3位专业领域及创新专家，记为E ₁、E ₂、E ₃。针对该企业基本情况、需求状况及候选伙伴的基本研发情况，再依据互补性（b₁）、兼容性（b₂）、创新资源（b₃）、创新能力（b₄）、创新环境（b₅）、声誉与信任（b₆）以及技术水平（b₇）这7大准则，对4个候选伙伴加以评价，按评价结果大小进行排序，从而选出最为合适的协同创新伙伴。在每个评价准则下，决策专家用犹豫模糊语言来表达自己的决策结果。在［0，1］内给出评分结果，描述评价指标的主要评分语言集P=｛“很差”=0.2，“差”=0.4，“一般”=0.5，“好”=0.6，“很好”=0.8｝。4位合作伙伴基本研发数据如表3所示。

表3 候选伙伴2020-2022年基本研发数据

研究对象	年份	已获得专利/件	发明专利	研发人员数量/人	人员占比/%	研发投入/元	投入占比/%
X ₁	2020	-	-	531	11.55	29 380 357.08	2.19
	2021	62	-	218	6.9	45 373 606.29	2.67
	2022	55	4	202	7.13	64 684 359.08	3.87
X ₂	2020	15	3	1 014	10.18	224 272 543.4	5.48
	2021	20	-	1 026	10.36	280 944 269.4	5.56
	2022	25	17	1 068	11.08	340 216 354.3	8.3
X ₃	2020	-	-	-	-	24 298 000	5.92
	2021	-	-	-	-	27 746 500	5.42
	2022	21	1	74	23.27	24 452 345.72	4.92
X ₄	2020	-	-	64	5.24	20 048 400	4.52
	2021	12	2	60	4.74	27 116 695.08	5.29
	2022	15	5	66	5	28 546 108.86	4.95

3.2 基于可能度矩阵的概率犹豫模糊EDAS评价步骤

（1）专家权重的计算

通过3位决策专家的社会信任关系，得到彼此之间的信任邻接矩阵为

A = E k E 1 E 2 E 3 E 1 - 0.7 0.2 E 2 0 - 0.4 E 3 0.3 0.5 -

由式（2）、（3）求得决策专家权重为：

λ 1 = 0.25

，

λ 2 = 0.5

，

λ 3 = 0.25

，即

λ k = (0.25,0.5,0.25)

。

（2）综合评价矩阵的计算

初始评价信息如表4~6所示。再利用上文PHFOWA算子求解综合评价矩阵，如表7所示。

表4 专家 $E 1$ 给出的评价矩阵 Q ₁

E ₁

b₁

b₂

b₃

b₄

b₅

b₆

b₇

X ₁

｛0.6（0.5），

0.8（0.5）｝

｛0.8（0.6），

0.9（0.4）｝

｛0.6（0.7），

0.7（0.3）｝

｛0.7（0.8），

0.8（0.2）｝

｛0.6（0.4），

0.8（0.6）｝

｛0.8（0.3），

0.9（0.7）｝

｛0.6（0.3），

0.8（0.7）｝

X ₂

｛0.7（0.4），

0.8（0.6）｝

｛0.4（0.3），

0.6（0.7）｝

｛0.7（0.7），

0.9（0.3）｝

｛0.3（0.4），

0.5（0.6）｝

｛0.7（0.6），

0.9（0.4）｝

｛0.6（0.6），

0.7（0.4）｝

｛0.7（0.8），

0.8（0.2）｝

X ₃

｛0.5（0.4），

0.6（0.6）｝

｛0.7（0.3），

0.8（0.7）｝

｛0.6（0.4），

0.8（0.6）｝

｛0.4（0.4），

0.5（0.6）｝

｛0.2（0.3），

0.4（0.7）｝

｛0.5（0.6），

0.7（0.4）｝

｛0.4（0.6），

0.6（0.4）｝

X ₄

｛0.6（0.8），

0.7（0.2）｝

｛0.6（0.4），

0.8（0.6）｝

｛0.7（0.8），

0.8（0.2）｝

｛0.4（0.4），

0.5（0.6）｝

｛0.4（0.5），

0.5（0.5）｝

｛0.6（0.8），

0.8（0.2）｝

｛0.5（0.5），

0.6（0.5）｝

表5 专家 $E 2$ 给出的评价矩阵 Q ₂

E ₂

b₁

b₂

b₃

b₄

b₅

b₆

b₇

X ₁

｛0.7（0.5），

0.8（0.5）｝

｛0.5（0.2），

0.7（0.8）｝

｛0.8（0.5），

0.9（0.5）｝

｛0.7（0.7），

0.8（0.3）｝

｛0.5（0.3），

0.7（0.7）｝

｛0.5（0.2），

0.7（0.8）｝

｛0.7（0.6），

0.9（0.4）｝

X ₂

｛0.4（0.7），

0.5（0.3）｝

｛0.7（0.7），

0.8（0.3）｝

｛0.5（0.2），

0.7（0.8）｝

｛0.6（0.7），

0.7（0.3）｝

｛0.5（0.5），

0.7（0.5）｝

｛0.5（0.2），

0.6（0.8）｝

｛0.6（0.3），

0.8（0.7）｝

X ₃

｛0.5（0.5），

0.6（0.5）｝

｛0.6（0.2），

0.7（0.8）｝

｛0.3（0.7），

0.5（0.3）｝

｛0.4（0.6），

0.5（0.4）｝

｛0.4（0.8），

0.6（0.2）｝

｛0.6（0.6），

0.7（0.4）｝

｛0.3（0.7），

0.5（0.3）｝

X ₄

｛0.6（0.8），

0.8（0.2）｝

｛0.3（0.8），

0.8（0.2）｝

｛0.2（0.5），

0.4（0.5）｝

｛0.5（0.7），

0.6（0.3）｝

｛0.3（0.5），

0.5（0.5）｝

｛0.4（0.8），

0.6（0.2）｝

｛0.5（0.5），

0.7（0.5）｝

表6 专家 $E 3$ 给出的评价矩阵 Q ₃

E ₃

b₁

b₂

b₃

b₄

b₅

b₆

b₇

X ₁

｛0.4（0.2），

0.6（0.8）｝

｛0.6（0.3），

0.8（0.7）｝

｛0.6（0.3），

0.8（0.7）｝

｛0.8（0.4），

0.9（0.6）｝

｛0.6（0.2），

0.7（0.8）｝

｛0.7（0.5），

0.9（0.5）｝

｛0.7（0.4），

0.8（0.6）｝

X ₂

｛0.6（0.4），

0.8（0.6）｝

｛0.5（0.2），

0.7（0.8）｝

｛0.7（0.5），

0.8（0.5）｝

｛0.4（0.2），

0.6（0.8）｝

｛0.6（0.5），

0.8（0.5）｝

｛0.5（0.6），

0.7（0.4）｝

｛0.6（0.5），

0.8（0.5）｝

X ₃

｛0.6（0.8），

0.7（0.2）｝

｛0.6（0.8），

0.7（0.2）｝

｛0.5（0.6），

0.6（0.4）｝

｛0.5（0.7），

0.6（0.3）｝

｛0.6（0.4），

0.8（0.6）｝

｛0.6（0.5），

0.7（0.5）｝

｛0.5（0.4），

0.6（0.6）｝

X ₄

｛0.7（0.7），

0.8（0.3）｝

｛0.4（0.7），

0.6（0.3）｝

｛0.4（0.8），

0.6（0.2）｝

｛0.4（0.7），

0.6（0.3）｝

｛0.4（0.6），

0.5（0.4）｝

｛0.6（0.6），

0.8（0.4）｝

｛0.6（0.6），

0.7（0.4）｝

表7 综合评价矩阵 Q

	b₁	b₂	b₃	b₄	b₅	b₆	b₇
X ₁	｛0.616 6（0.4），0.762 2 （0.6）｝	｛0.623 9（0.366 7），0.794 0（0.633 3）｝	｛0.717 2（0.5），0.843 5（0.5）｝	｛0.728 9（0.633 3），0.831 8（0.366 7）｝	｛0.552 8（0.3），0.728 9（0.7）｝	｛0.650 0（0.333 3），0.826 8（0.666 7）｝	｛0.677 6（0.433 3），0.858 6（0.566 7）｝
X ₂	｛0.544 1（0.5），0.683 8 （0.5）｝	｛0.594 6（0.4），0.736 8（0.6）｝	｛0.612 7（0.466 7），0.794 0（0.533 3）｝	｛0.490 9（0.433 3），0.633 7（0.566 7）｝	｛0.583 8（0.533 3），0.794 0（0.466 7）｝	｛0.527 1（0.466 7），0.653 6（0.533 3）｝	｛0.627 8（0.533 3），0.8（0.466 7）｝
X ₃	｛0.527 1（0.566 7），0.627 8（0.433 3）｝	｛0.627 8（0.433 3），0.728 9（0.566 7）｝	｛0.440 5（0.566 7），0.623 9（0.433 3）｝	｛0.426 7（0.566 7），0.527 1（0.433 3）｝	｛0.417 4（0.5），0.627 8（0.5）｝	｛0.577 1（0.566 7），0.7（0.433 3）｝	｛0.380 8（0.566 7），0.552 8（0.433 3）｝
X ₄	｛0.627 8（0.766 7），0.778 7（0.233 3）｝	｛0.414 4（0.633 3），0.762 2（0.366 7）｝	｛0.417 4（0.7），0.588 0（0.3）｝	｛0.452 3（0.6），0.577 1（0.4）｝	｛0.351 9（0.533 3），0.5（0.466 7）｝	｛0.510 1（0.733 3），0.717 2（0.266 7）｝	｛0.527 1（0.533 3），0.677 6（0.466 7）｝

（3）指标权重的计算

1）客观权重

w j'

依据综合矩阵利用式（4）求解出其得分函数，如表8所示。

表8 得分函数

	b₁	b₂	b₃	b₄	b₅	b₆	b₇
X ₁	0.703 9	0.731 7	0.780 3	0.766 6	0.676 1	0.767 9	0.780 2
X ₂	0.613 9	0.679 9	0.709 4	0.571 8	0.681 9	0.594 6	0.708 2
X ₃	0.570 7	0.685 1	0.520 0	0.470 2	0.522 6	0.630 3	0.455 3
X ₄	0.663 0	0.541 9	0.468 6	0.502 2	0.421 0	0.565 3	0.597 3

依据式（5）、（6）求得指标客观权重为

w j' =

（0.077 7，0.099 5，0.194 9，0.166 1，0.162 2，0.111 5，0.188 1）

2）主观权重

w j

依据前文客观权重的计算可得，最好为b₃，最差为b₁，分别基于最好和最差，与剩余指标加以打分对比，结果如表9所示。

表9 指标结果

b₁	b₂	b₃	b₄	b₅	b₆	b₇
9	6	1	3	4	5	2
1	2	9	7	6	7	8

依据式（7）、（8）构造最优化模型，模型为

m i n ς

s . t . w 3 - 9 w 1 ≤ ς; w 3 - 6 w 2 ≤ ς; w 3 - 3 w 4 ≤ ς; w 3 - 4 w 5 ≤ ς; w 3 - 5 w 6 ≤ ς; w 3 - 2 w 7 ≤ ς; w 2 - 2 w 1 ≤ ς; w 4 - 7 w 1 ≤ ς; w 5 - 6 w 1 ≤ ς; w 6 - 7 w 1 ≤ ς; w 7 - 8 w 1 ≤ ς ∑ j = 1 7 w j = 1, w j ≥ 0

利用LINGO对上述模型加以求解，可得

ς = 0.099

，通过式（9）计算可得CR<0.25，可见给出的指标对比关系符合一致性检验结果。指标主观权重

w j

为

w j =

（0.026 6，0.072 9，0.338 7，0.146 0，0.109 4，0.087 5，0.218 9）

3）指标综合权重

w b j

由式（10）可得

w b j =

（0.052 1，0.086 2，0.266 8，0.156 1，0.135 8，0.099 5，0.203 5）

（4）基于可能度矩阵求解平均解

利用式（11），将每个评价指标下的评价值两两比较，得可能度矩阵结果如下

P 1 = 0.5 0.660 6 0.780 9 0.540 2 0.339 4 0.5 0.723 6 0.433 6 0.219 1 0.276 4 0.5 0.358 6 0.459 8 0.566 4 0.641 4 0.5

P 2 = 0.5 0.554 0 0.556 1 0.825 8 0.446 0 0.5 0.492 6 0.811 9 0.443 9 0.507 4 0.5 0.952 6 0.174 2 0.188 1 0.047 4 0.5

P 3 = 0.5 0.676 6 11 0.323 4 0.5 1 0.975 1 00 0.5 0.688 1 0 0.024 9 0.311 9 0.5

P 4 = 0.5 0.82 15 11 0.178 5 0.5 0.817 9 0.686 1 0 0.182 1 0.5 0.203 7 0 0.313 9 0.796 3 0.5

P 5 = 0.5 0.492 7 0.670 6 0.826 9 0.507 3 0.5 0.984 8 1 0.329 4 0.015 2 0.5 0.836 9 0.173 1 0 0.163 1 0.5

P 6 = 0.5 0.698 2 0.692 1 0.695 8 0.301 8 0.5 0.358 7 0.551 3 0.307 9 0.641 3 0.5 0.657 3 0.304 2 0.448 7 0.342 7 0.5

P 7 = 0.5 0.653 8 1 0.900 4 0.346 2 0.5 11 00 0.5 0 0.099 6 01 0.5

依据得出的可能度矩阵，利用式（12）可得各指标的整体优势度为

P X 11' = 1.981 6

、

P X 21' = 1.496 6

、

P X 31' = 0.854 1

、

P X 41' = 1.667 7

；

P X 12' = 1.930 6

、

P X 22' = 1.750 5

、

P X 32' = 1.903 8

、

P X 42' = 0.409 7

；

P X 13' = 2.676 6

、

P X 23' = 2.298 5

、

P X 33' = 0.688 1

、

P X 43' = 0.336 7

；

P X 14' = 2.821 5

、

P X 24' = 1.682 5

、

P X 34' = 0.385 8

、

P X 44' = 1.110 2

；

P X 15' = 1.990 2

、

P X 25' = 2.492 1

、

P X 35' = 1.181 5

、

P X 45' = 0.336 2

；

P X 16' = 2.086 1

、

P X 26' = 1.211 7

、

P X 36' = 1.606 6

、

P X 46' = 1.095 6

；

P X 17' = 2.554 2

、

P X 27' = 2.346 2

、

P X 37' = 0

、

P X 47' = 1.099 6

根据

P i j' (i = 1, … 4, j = 1, … 7)

的值对各个指标的值进行比较，结果如下。

X 11 > 0.540 2 X 41 > 0.566 4 X 21 > 0.7236 X 31

；

X 12 > 0.556 1 X 32 > 0.507 4 X 22 > 0.811 9 X 42

；

X 13 > 0.676 6 X 23 > 1 X 33 > 0.688 1 X 43

；

X 14 > 0.821 5 X 24 > 0.686 1 X 44 > 0.796 3 X 34

；

X 25 > 0.507 3 X 15 > 0.670 6 X 35 > 0.836 9 X 45

；

X 16 > 0.692 1 X 36 > 0.641 3 X 26 > 0.551 3 X 46

；

X 17 > 0.653 8 X 27 > 1 X 47 > 1 X 37

在各个比较结果下，依据排序中第2个和第3个评价值，利用式（13）求得平均解如下所示。

A V 1 = {0.415 2 0.5, 0.465 0 (0.5)}

；

A V 2 = {0.424 6 0.5, 0.464 3 (0.5)}

；

A V 3 = {0.391 7 0.5, 0.461 3 (0.5)}

；

A V 4 = {0.360 6 0.5, 0.422 5 (0.5)}

；

A V 5 = {0.369 7 0.5, 0.449 5 (0.5)}

；

A V 6 = {0.400 0 0.5, 0.448 0 (0.5)}

；

A V 7 = {0.412 0 0.5, 0.467 8 (0.5)}

；

（5）正向PDA、反向NDA距离矩阵

本文所涉及指标均为效益型指标，依据式（14）、（15）依次得到正向距离矩阵PDA及反向距离矩阵NDA，如表10~11所示。

表10 正向距离矩阵

PDA	b₁	b₂	b₃	b₄	b₅	b₆	b₇
X ₁	0.599 6	0.646 3	0.585 3	0.957 8	0.905 0	0.811 0	0.773 5
X ₂	0.395 0	0.529 9	0.599 0	0.460 3	0.731 9	0.402 2	0.609 8
X ₃	0.296 9	0.541 5	0.225 4	0.200 9	0.269 4	0.486 6	0.035 1
X ₄	0.506 4	0.219 3	0	0.282 5	0.143 9	0.333 2	0.357 9

表11 反向距离矩阵

NDA	b₁	b₂	b₃	b₄	b₅	b₆	b₇
X ₁	0	0	0	0	0	0	0
X ₂	0	0	0	0	0	0	0
X ₃	0	0	0	0	0	0	0
X ₄	0	0	0.012 7	0	0	0	0

（6）加权PDA总和与加权NDA总和

利用式（16）、（17）求得

S P 1 = 0.753 6

、

S P 2 = 0.561 4

、

S P 3 = 0.245 8

、

S P 4 = 0.214 9

S N 1 = 0

、

S N 2 = 0

、

S N 3 = 0

、

S N 4 = 0.003 4

（7）待选伙伴的综合评价值

A S i

由式（18）可得

A S 1 = 0.994 5

、

A S 2 = 0.868 4

、

A S 3 = 0.661 3

、

A S 4 = 0.195 2

即

A S 1 > A S 2 > A S 3 > A S 4

，所以对于某企业最为合适的协同创新伙伴为

X 1

。

3.3 对比分析

为了对比所提方法的可行性，将利用TOPSIS、VIKOR、 PHFWA与PHFWG算子对本文算例进行计算，排序结果如表12所示。

表12 对比结果

方法	排序结果
TOPSIS	$A S 1 > A S 3 > A S 2 > A S 4$
VIKOR	$A S 1 > A S 2 > A S 3 > A S 4$
PHFWA算子	$A S 1 > A S 2 > A S 4 > A S 3$
PHFWG算子	$A S 1 > A S 2 > A S 4 > A S 3$
本文	$A S 1 > A S 2 > A S 3 > A S 4$

分析可知其他方法计算与本文方法所得结果略有差异，但其他方法的计算过程更为繁琐复杂，而本文所提模型求解过程相对简单且易于理解，所求结果更为准确。

4 结论与建议

4.1 结论

本文鉴于高端装备制造业协同创新伙伴选择的必要性、复杂性及决策多样性等问题，构建了高端装备制造业协同创新伙伴选择指标体系，提出一种基于可能度的EDAS群决策方法，并将该方法应用于上述指标体系下的备选伙伴的评价测度。实证结果表明，该模型相对于TOPSIS等方法，计算更简便准确，更好地满足了高端装备制造业协同创新伙伴选择需求。本文提出了一套切实可行的方案指导其进行协同创新伙伴选择，具体如下：

（1）构建高端装备制造业协同创新伙伴选择指标体系。指标体系主要包括7个一级指标与19个二级指标，不仅考虑了协同创新伙伴选择的常用指标，如：互补性、兼容性、声誉与信任及技术水平，更是结合高端装备制造业协同创新发展情况与现实需求，充分考虑创新资源、创新能力与创新环境等因素，更好地满足了高端装备制造业协同创新伙伴选择决策的实际需要。

（2）对评价信息进行优化处理。考虑到决策者评价的不确定性及各指标间关联性，本文使用概率犹豫模糊集处理专家初始评价结果，加入概率因素在更大程度上保留并完善初始评价信息，优化评价结果。

（3）建立基于可能度的EDAS群决策模型。将主观权重和客观权重相结合，避免了主、客观赋权单独使用的缺点，为高端装备制造业协同创新伙伴选择提供了有效的解决方案。通过进一步的实证分析与对比分析，验证了该方法适用于高端装备制造业协同创新伙伴选择情景，其评价决策结果更加准确，可为高端装备制造相关企业选择协同创新伙伴提供可靠的决策参考。

4.2 建议

依据本文指标构建过程以及实证分析过程，得出以下几点建议：

（1）伙伴选择指标标准化。在通用评价指标的基础上，结合现实创新动态以及自身创新情况，制定一套明确的合作伙伴选择标准，确保选择的合作伙伴真正符合需求。

（2）伙伴选择流程规范化。首先，核心企业结合自身现实情况与需求，制定出协同创新目标，确定所需的资源与技术；然后，初步选择出可以提供技术、资源或市场支持的备选伙伴；最后，对备选伙伴从多个评价维度进行综合评估，确定最为合适的合作伙伴。

（3）完善保障机制。首先，多参与创新企业交流活动，加强与各主体间的互动，增进彼此信任度；其次，要加强建立明确的合作机制与沟通渠道，明确各参与方的责任和权利，制定合理的合作计划，以确保合作的顺畅与高效；最后，制定公平公正的协同创新利益协调和风险防范机制。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	王金，陈楠希，周华，等.数字经济冲击下高端装备制造业数字化转型研究[J].西南金融，2023(7)：65-80.

2	焦智博.装备制造业协同创新网络结构演化与空间特征研究：黑龙江1985-2017年专利数据分析[J].科技进步与对策，2018，35(21)：57-64.

3	占永志.基于场理论的企业创新生态伙伴选择研究[J].科技和产业，2023，23(11)：77-84.

4	李军，朱先奇，王丽霞.集群企业协同创新伙伴选择研究：基于知识能力的评价指标体系和改进的ELMAN神经网络模型[J].预测，2020，39(5)：23-29.

5	Reusen E， Stouthuysen K.Trust transfer and partner selection in interfirm relationships[J].Accounting，Organizations and Society，2020，81（2）：101081.

6	成鹏飞，熊宇林，成思婕，等.基于多新异构VIKOR方法的大学科技城协同创新伙伴选择研究[J].湖南财政经济学院学报，2023，39(3)：56-69.

7	卢梅，李卓元.国际工程EPC总承包商联合体伙伴优选研究：基于任务和情境视角[J].西安建筑科技大学学报（自然科学版），2019，51(1)：147-154.

8	周向红，李丹萍，成鹏飞，等.面向云制造协同创新伙伴选择的多源异构VIKOR群决策方法[J].计算机集成制造系统，2022，28(1)：59-72.

9	Guo B， Hao S Y， Zhang Y，et al.An entropy weight‑topsis based model for partner selection of strategic alliance of prefabricated construction enterprises[J].Discrete Dynamics in Nature and Society，2022，2022（1）：7844524.

10	Shevtshenko E， Mahmood K， Karaulova T.Enhan-cing the partner selection process in a sustainable partner network[J].International Federation of Automatic Control，2019，52(13)：2425-2430.

11	Santos R S， Soares J， Marques P C，et al.Integra-ting business，social，and environmental goals in open innovation through partner selection[J].Sustainability，2021，13(22)：12870.

12	Arsanti T A， Rupidara N S， Bondarouk T.How to find the right partner？open innovation partner selection process[J].Administrative Sciences，2022，12(4)：165.

13	Chowdhury ，S.，Das，S. Multi-stage partner selection for firms'non-core offerings： a study of the telecom sector of India ［EB/OL］.（2022-09-16）［2023-10-15］.

14	Li B， Zhang J H.A cooperative partner selection study of military‑civilian scientific and technological collaborative innovation based on interval‐va-lued intuitionistic fuzzy set[J].Symmetry，2021，13(4)：553.

15	刘澜，黄豪.基于最优决策的国际铁路多式联运合作伙伴选择模型[J].中国铁道科学，2019，40(5)：110-117.

16	李柏洲，高硕.企业合作型原始创新互惠共生伙伴选择研究[J].哈尔滨工程大学学报，2019，40(7)：1367-1374.

17	李柏洲，尹士.数字化转型背景下ICT企业生态伙伴选择研究：基于前景理论和场理论[J].管理评论，2020，32(5)：165-179.

18	李翠，王爱敏，倪渊.基于生态位理论的企业协同创新伙伴选择研究[J].北京城市学院学报，2018(4)：41-47.

19	孟贤，鲍红焉，石孟宇，等.基于区块链的电网物资供应链合作伙伴选择[J].计算机仿真，2023，40(12)：434-440，469.

20	刘嘉，汪永超，陈坤.基于CRITIC算法的绿色制造合作伙伴选择[J].工具技术，2021，55(2)：43-47.

21	李红艳，吴忠，王静.基于ANP-DEA-GRA的协同创新合作伙伴选择[J].计算机工程与应用，2017，53(24)：238-244，251.

22	黄哲，刘玉颖.产业联盟实现创新的伙伴选择策略[J].学术交流，2018，34(8)：86-92.

23	冯向前，叶银萍，李金生.基于模糊EDAS的中小企业绿色创新障碍分析[J].科技管理研究，2020，40(11)：200-205.

24	武文颖，李应，金飞飞，等.基于概率犹豫信息集成方法的群决策模型[J].模式识别与人工智能，2017，30(10)：894-906.

25	骆华.基于改进距离的概率犹豫模糊多属性决策方法[J].武汉理工大学学报（信息与管理工程版），2020，42(3)：239-245.

26	同思蓉，孙秉珍，赵萌，等.基于BWM与愿景效用函数的多属性群决策模型[J].系统科学与数学，2023，43(10)：2573-2597.

27	Song H F， Chen Z C.Multi‑attribute decision‐ma-king method based distance and COPRAS method with probabilistic hesitant fuzzy environment[J].International Journal of Computational Intelligence Systems，2021，14(1)：1229-1241.

28	彭定洪，董婷婷，张文华.企业绿色创新能力评价的简约式HF-EDAS方法[J].统计与决策，2023，39(3)：183-188.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 高端装备制造业协同创新伙伴选择评价指标构建

1.1 伙伴选择评价指标体系建立过程

表1 国内外创新伙伴选择评价指标

图1 创新伙伴选择评价指标体系建立过程

1.2 评价指标体系的确定

图2 高端装备制造业协同创新伙伴选择评价指标体系

2 高端装备制造业协同创新伙伴选择评价模型构建

2.1 评价矩阵

2.1.1 问题描述

2.1.2 评价矩阵聚合

2.2 权重计算

2.2.1 基于社会网络信任关系的决策专家权重计算

图3 社会网络关系

2.2.2 评价指标权重计算

表2 1~9标度所对应的一致性指数

2.3 基于可能度矩阵的概率犹豫模糊EDAS决策方法

2.3.1 可能度矩阵

2.3.2 EDAS决策排序

3 算例分析

3.1 算例应用

表3 候选伙伴2020-2022年基本研发数据

3.2 基于可能度矩阵的概率犹豫模糊EDAS评价步骤

表4 专家 E 1给出的评价矩阵 Q 1

表5 专家 E 2给出的评价矩阵 Q 2

表6 专家 E 3给出的评价矩阵 Q 3

表7 综合评价矩阵 Q

表8 得分函数

表9 指标结果

表10 正向距离矩阵

表11 反向距离矩阵

3.3 对比分析

表12 对比结果

4 结论与建议

4.1 结论

4.2 建议

参考文献

表4 专家 $E 1$ 给出的评价矩阵 Q ₁

表5 专家 $E 2$ 给出的评价矩阵 Q ₂

表6 专家 $E 3$ 给出的评价矩阵 Q ₃