高维数据聚类数量可视化确定模式

何选森; 何帆; 樊跃平; 陈洪军

doi:10.3969/j.issn.2095-1248.2024.03.010

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 3: 71 - 84

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.03.010

信息科学与工程

高维数据聚类数量可视化确定模式

何选森 ^,¹^,² ,
何帆 ³ ,
樊跃平 ¹ ,
陈洪军 ¹

展开

^1. 广州商学院信息技术与工程学院, 广州 511363
^2. 湖南大学信息科学与工程学院, 长沙 410082
^3. 北京理工大学管理与经济学院, 北京 100081

何选森(1958-),男,河南灵宝人,教授,主要研究方向:机器学习,E-mail: xshe2010@163.com。

收稿日期: 2024-01-03

网络出版日期: 2024-08-30

基金资助

广东省普通高校重点领域专项(2021ZDZX1035)

收起

Visualized determination mode for clustering quantity of high-dimensional data

Xuansen HE ^,¹^,² ,
Fan HE ³ ,
Yueping FAN ¹ ,
Hongjun CHEN ¹

Expand

^1. School of Information Technology and Engineering，Guangzhou College of Commerce，Guangzhou 511363，China
^2. College of Information Science and Engineering，Hunan University，Changsha 410082，China
^3. School of Management and Economics，Beijing Institute of Technology，Beijing 100081，China

Received date: 2024-01-03

Online published: 2024-08-30

Fold

摘要

为了解决经典K-均值聚类算法要求用户事先知道待处理数据的聚类数量及聚类结果对算法的初始化很敏感的问题，提出一种对K-均值聚类算法的改进措施并可视化地确定聚类数量的综合方案。首先，对数据进行标准化，使其服从正态分布，利用主分量分析（principal component analysis，PCA）抽取数据中最重要的特征以实现高维数据的降维；然后，采用最远质心选择和最小-最大距离规则对K-均值聚类算法的初始化进行修正，避免出现空聚类并确保数据的可分离性；在此基础上，采用统计经验法则估计聚类数量的可能范围，通过搜索在此范围内平方误差和（sum-of-squared-error， SSE）曲线的肘部估计最佳的聚类数量；最后，通过计算比较各个聚类的轮廓系数以评价算法的聚类质量，从而最终确定数据集固有的聚类数量。仿真结果表明，该方案不仅能可视化地确定数据集潜在的聚类数量，而且为大数据时代的高维数据分析提供了一种有效的方法。

关键词： K-均值聚类算法; 主分量分析; 最远质心选择; 最小-最大距离规则; 统计经验法则; 肘部法; 轮廓分析

本文引用格式

何选森 , 何帆 , 樊跃平 , 陈洪军 . 高维数据聚类数量可视化确定模式[J]. 沈阳航空航天大学学报, 2024 , 41(3) : 71 -84 . DOI: 10.3969/j.issn.2095-1248.2024.03.010

Abstract

In order to solve the problem that the classical K-means clustering algorithm reguired users to know the number of clusters in advance and the clustering results were sensitive to initialization of the algorithm， a comprehensive scheme was proposed to improve the random initial partitioning of K-means algorithm and visually determine the number of clusters. Firstly， the data was standardized to make it obey normal distribution， and the most important features were extracted by principal component analysis to achieve dimensionality reduction of high-dimensional data. Then， the farthest centroid selection and min-max distance rule were used to modify the random initialization of K-means algorithm to avoid empty clusters and ensure data separability. Based on these， the statistical empirical rule was used to estimate the range of the number of clusters， and the optimal number of clusters was assessed by searching the elbow of sum-of-squared-error curve within this range. Finally， by calculating and comparing the silhouette coefficients of each cluster， the clustering quality of the algorithm was evaluated， thereby ultimately determining the inherent number of clusters in the data. The simulation results show that the proposed scheme can not only visually determine the potential number of clusters in the data， but also provide an effective method for high-dimensional data analysis in the era of big data.

Key words： K-means clustering algorithm; principal component analysis; farthest centroid selection; min-max distance rule; statistical empirical rule; elbow method; silhouette analysis

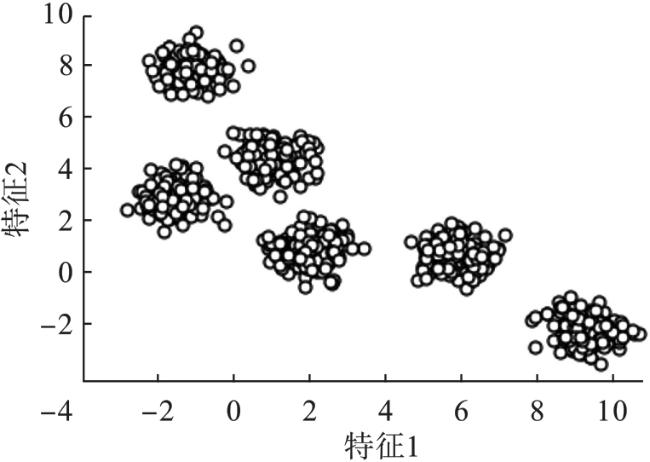
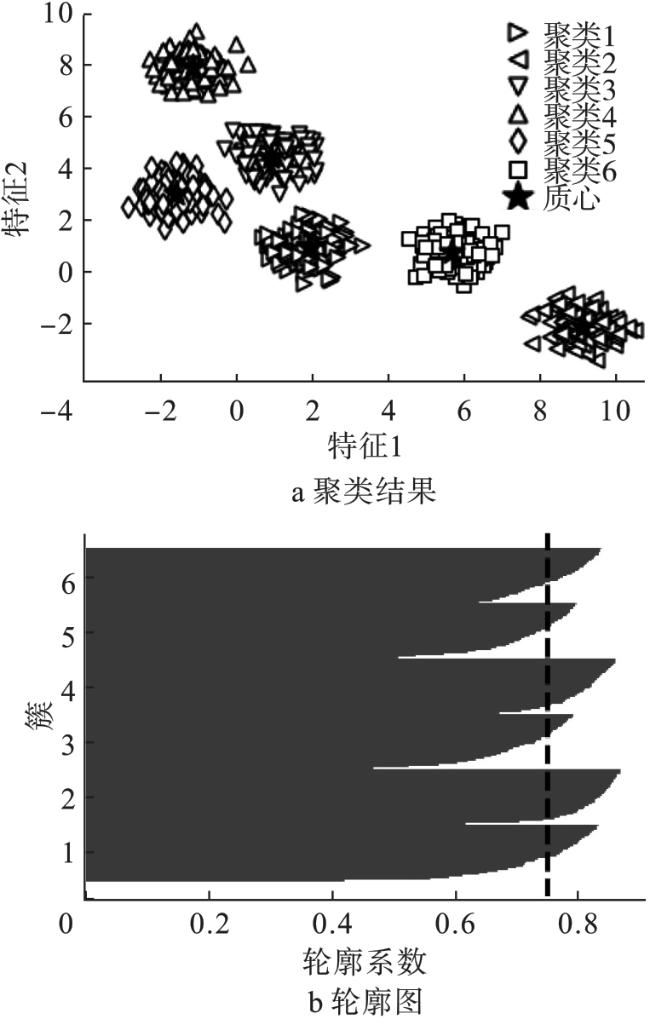
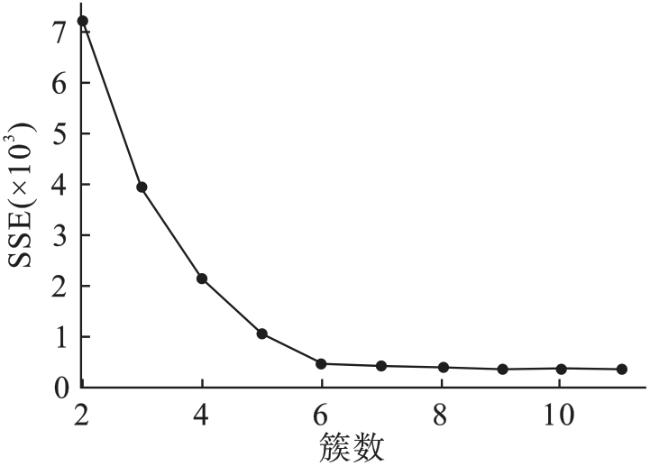
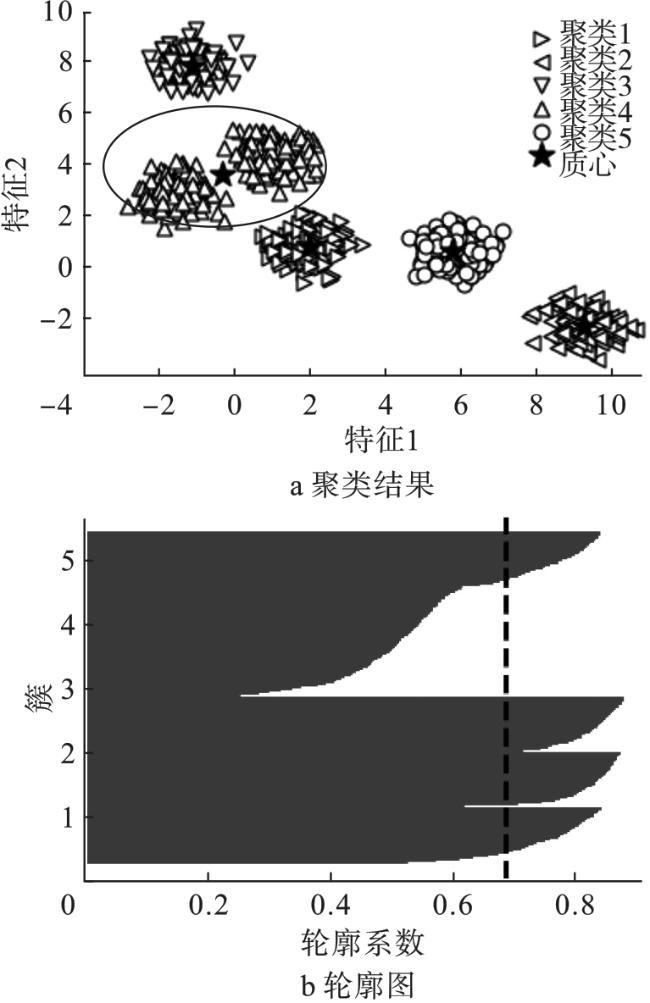
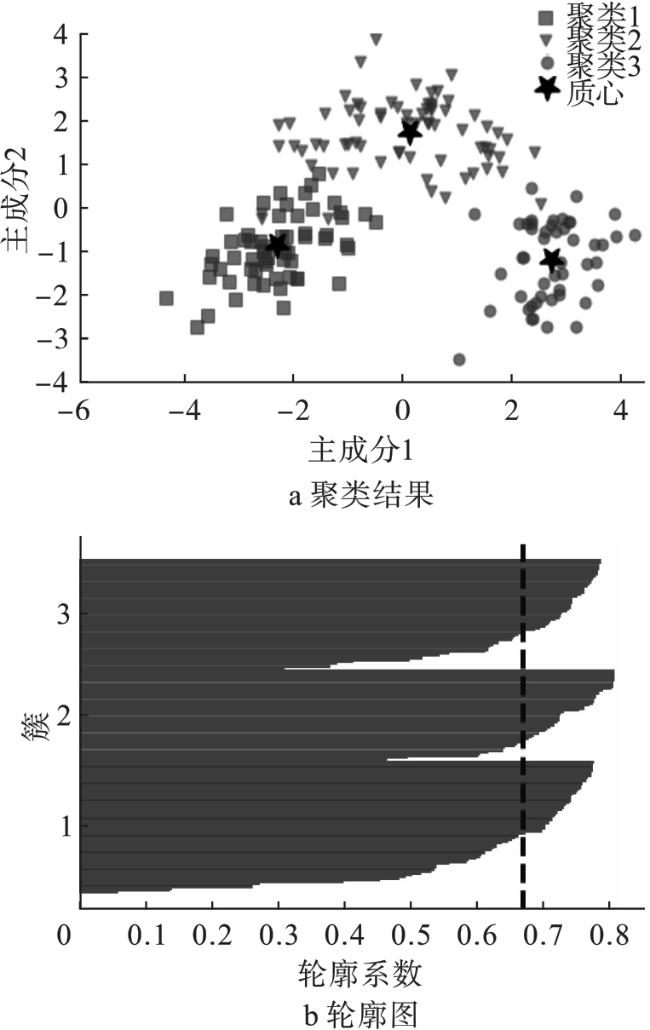
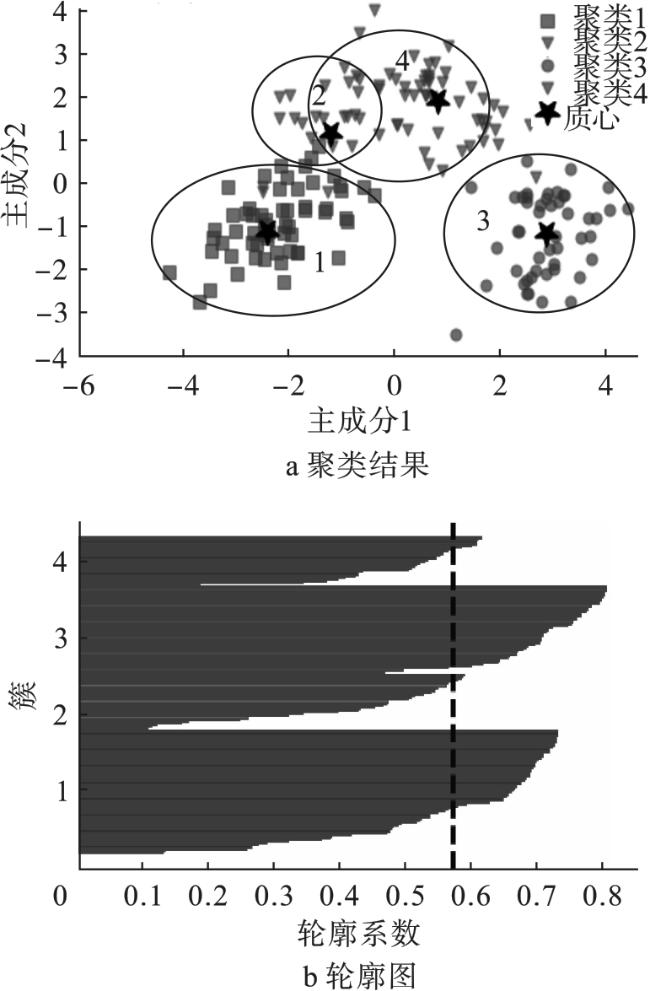
随着智能手机的普及和自媒体的蓬勃发展，大数据时代下人们对数据分析^［1］的需求更加迫切和必要。狭义数据分析是用统计法对数据进行处理、归纳并提炼数据的有用信息，从而为管理决策提供支持。广义数据分析包括狭义数据分析和数据挖掘。利用多元统计方法挖掘隐藏在数据背后的、潜在的信息的过程称为数据挖掘^［2］。在数据分析中，最基本的任务是对数据分类，它主要包括监督学习和无监督学习两种。监督分类中的数据具有类标签（即具有答案），并将数据划分为训练集和测试集，通过训练数据建立一个分类器模型，采用测试集对模型进行修正，使用该模型对未知数据的所属类进行预测^［3］。模式识别和机器学习^［4］的主要内容也是建立监督学习的分类器。然而，在实际中，原始数据是采用各种传感器检测获取的，没有可用的类标签，因此需要采用无监督学习方法。主要的无监督分类是聚类（clustering）^［5］或称探索性数据分析。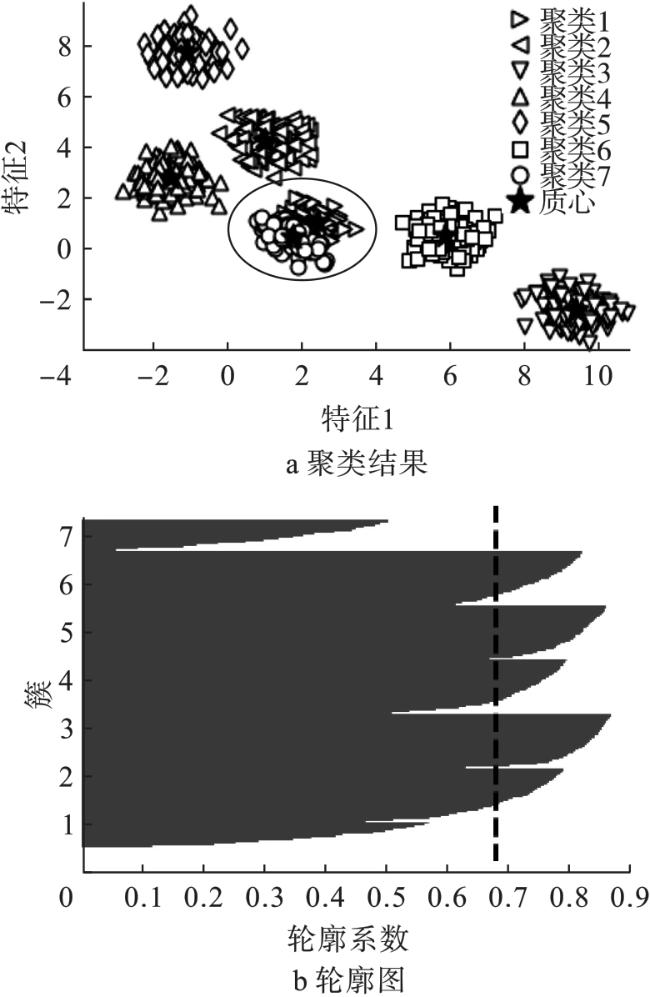聚类技术是将未标记的数据划分成有限的、离散的数据子集^［5］，最大的优势是能够发现数据固有的聚类结构，而不要求原始数据提供类标签信息。按照数据点之间的相似性^［6］，聚类把数据划分成不同的簇或集群（或组），使得同一簇中数据具有最大的相似性，而具有相异性的数据能被明确地分离开来。根据所生成的数据簇特性，聚类可分为层次聚类和分区聚类。层次聚类是用嵌套分区序列对整个数据集进行分类，从每个数据点作为一个单独集群逐步合并，直到所有样本点都属于同一个聚类的过程称为凝聚层次聚类；与之相反，由所有数据点为一个集群逐步划分到每个样本，形成一个单独聚类的过程称为分裂层次聚类。在没有分层结构的情况下，直接将数据点划分为预先指定数量集群的方法，称为分区聚类。在实际中，应用最为广泛的聚类是分区聚类，而其中最著名且经典的方法是K-均值聚类算法^［7-8］及其改进版本。

在数据聚类分析中，经典K-均值聚类算法具有易于执行且它的计算效率高的特点，获得了广泛的应用，然而它也有两个主要缺陷^［9-10］：一是聚类结果对算法随机所选择的聚类中心非常敏感，即不同的初始选择将影响算法最终所产生的收敛质心；二是在无推理前提下，用户需要指定数据的聚类数量，这对于现实世界中复杂、未知的数据集来说是不可能的。

为解决K-均值聚类算法的问题，很多学者提出了相应的改进方案。针对随机初始化问题，依据变异系数最大值和相关绝对值的最小值，通过选择两个主变量来计算初始聚类中心^［11］；采用初始种子选择算法以确定数据的初始划分^［12］；利用鲁棒密度初始化将种子点定位在数据集的密集区域以实现聚类的初始化^［13］；在算法每次运行中，使用数据的一个属性创建一个初始聚类，并将多次运行的聚类结果组合起来形成初始的划分^［14］。在确定聚类数量方面，将最大稳定集与连续Hopfield网络相结合估计聚类数量^［15］；为提高差分进化自动聚类（automatic clustering using differential evolution，ACDE）的性能，使用U-控制图法，结合ACDE以确定聚类数量^［16］；基于查找聚类均值有效性的聚类指数，结合核心函数指数及均值性质确定新的聚类中心和聚类数量^［17］；通过计算基于中心点的偏差比指数（deviation ratio index，DRI）来确定聚类的数量^［18］；在数据分区之前，利用相似性矩阵的易感性确定最佳的聚类数量^［19］。

从以上分析可知，无论是随机初始化，还是确定数据集的聚类数量，对K-均值聚类算法的聚类结果都将产生很大影响。为此，本文提出最远质心选择和最小-最大距离规则对K-均值聚类算法进行改进；通过标准化和主分量分析的预处理实现数据的降维；利用统计经验法则和肘部法初步估计数据集的聚类数量，并采用轮廓分析法评估聚类的质量，最终确定数据集本身所固有的聚类数量。

1 特征缩放与主分量提取

设数据特征数量为p，样本容量为n，将数据表示为矩阵 X =｛x_ik |i=1， 2， …， n； k=1， 2， …， p｝，其中 X 的每一行是一个样本 x _i （i=1， …， n），每一列是一个特征 x _k （k=1， …， p）。

在聚类分析中，采用L ₂范数即欧几里得（欧氏）距离来测度数据点的远近，如式（1）所示。

D (x i, x j) = ∑ k = 1 p (x i k - x j k) 2

（1）

式中： x_ik 和x_jk 分别表示数据样本 x _i 和 x _j 的第k个特征值。数据不同特征的取值差别可能很大，甚至它们的度量单位也可能不同。为此，要对数据特征进行缩放的预处理。最典型的缩放包括归一化和标准化。归一化使得特征的取值在［0，1］之间，而标准化使得数据特征服从标准的正态分布N（0，1）。数据特征的标准化为

x j k s t d = x j k σ k

（2）

式中： x_jk 为样本点 x _j 的第k个特征； σ _k 为第k个特征列的标准差。

对高维数据的压缩（即降维）也是必要的数据预处理，其方法包括监督的线性判别分析、主分量分析^［20］、非线性的核PCA等。由于聚类属于无监督的线性模型，考虑到数据标准化后服从正态分布，且PCA的先决条件也是对数据进行标准化预处理^［21］。因此，本文采用PCA实现数据压缩。

设数据 X 包含K个聚类，某个聚类C_k （k=1，…，K）对应于第j个特征的质心（centroid） m _k 为

m k = 1 n k ∑ i = 1 n k x i j

（3）

式中： n_k 为聚类C_k 中的样本数量； m _k 为 X 中某一特征列的样本均值。

对数据 X，两个特征 x _l 和 x _k 的协方差为

σ l k = 1 n ∑ i = 1 n [(x i l - m l) (x i k - m k)]

（4）

式中： m _l 和 m _k 分别为特征 x _l 和 x _k 的样本均值。在数据标准化条件下，由于样本均值为零，因此数据的统计特性由样本方差及不同特征间的协方差表示，数据 X 对应的p×p维协方差矩阵 Σ =｛σ_lk | l， k=1， 2， …， p｝，它的主对角元素为各个特征的方差σ_i ²（i=1， 2， …， p）。对 Σ 进行特征分解可获得特征值λ和对应的特征向量 v （即PCA中的主分量）。协方差矩阵 Σ 的特征向量 v 和特征值 λ 满足关系

Σ v = λ v

（5）

式中：特征值是由标量组成的向量 λ =（λ ₁， λ ₂，…，λ_p ），它和特征向量 v 的数量是相同的，都是p维。

PCA通过选择代表主分量信息（即方差）所对应的特征向量的子集来实现数据压缩^［22］。特征向量包含的信息由其特征值大小决定。因此，可按照特征值从大到小的次序排列其所对应的特征向量，其中某一个特征值λ_k （k=1， 2， …， p）的方差解释比计算为

R k = λ k ∑ k = 1 p λ k

（6）

根据各特征值对应R_k 值的大小，假设选择前q（q<<p）个特征值对应的特征列向量构成投影矩阵

W = [E 1 E 2 ⋯ E q]

（7）

式中： E ₁是R_k 处在最大位置上的特征向量， E ₂是R_k 处在第二大位置上的特征向量，依此类推。PCA要求所选取的前q个特征向量必须占据整个方差解释率中的大部分。

将原始数据矩阵 X 乘以投影矩阵 W，就实现了把 X 从p维降低到q维的特征子空间上，如式（8）所示。

X s u b = X W

（8）

2 K -均值聚类算法的初始化改进

经典K-均值聚类算法基本迭代步骤^［9-10］如下：

（1）对于具有K个聚类的数据 X，随机选择K个数据点作为初始聚类质心向量矩阵 m _k （k=1， 2，…， K）；

（2）按照距离最邻近原则，将其他数据点分配给邻近的质心，形成K个聚类C_k （k=1， 2， …， K）；

（3）根据当前所划分的数据结构，遵循式（3）重新计算（即更新）每个聚类中数据的质心；

（4）重复步骤（2）和（3），直到相邻两次更新的聚类中心不发生变化，或达到指定的最大迭代次数。

对于分区型聚类算法，最常用的误差度量是平方误差和SSE）^［10］

S S E = ∑ i = 1 n ∑ j = 1 K γ i j | | x i - m j | | 22

（9）

式中：||∙||₂表示L ₂范数。如果数据点 x _i 属于聚类C_j，则权重γ_ij =1，否则γ_ij =0，即SSE本质上是聚类内部的SSE。

由K-均值聚类算法的迭代步骤可知，初始聚类中心是随机选择的，这使得一些中心之间可能相距很近，因而在后续的迭代过程中这些聚类会被合并，从而出现了空聚类。

首先计算任意两数据点欧氏距离，并把距离最远的两个点（假设为 x ₁和 x ₂）作为初始质心，如式（10）所示。

D (x 1, x 2) = m a x D (x i, x j) (i, j = 1,2, ⋯, n)

（10）

式中：D（ x ₁， x ₂）为初始两个质心 x ₁和 x ₂之间距离。显然，该距离是所有数据点对（ x _i， x _j ）（i， j=1， 2， …， n）距离中的最大值，即采用最远质心选择原则。然后，以这两个中心为出发点，利用最小-最大距离规则选择下一个（第3个）中心 x ₃，如式（11）所示。

m i n D (x 3, x r) = m a x D (x i, x r) (r = 1,2; i ≠ 1,2)

（11）

即第3个中心 x ₃与前两个中心（ x ₁， x ₂）距离中的最小者为其他数据点 x _i （i≠1， 2）与（ x ₁， x ₂）距离中的最大者。同样地，在这3个中心（ x ₁， x ₂， x ₃）所组成的3元组的基础上，仍然利用最小-最大距离规则选择下一个（即第4个）聚类中心 x ₄，如式（12）所示。

m i n D (x 4, x r) = m a x D (x i, x r) (r = 1,2, 3; i ≠ 1,2, 3)

（12）

依此类推，即可选择其余的聚类中心。

采用式（10）~（12）对K-均值聚类算法改进，确保了算法的初始质心之间是完全可分离的，即使后续算法的不断迭代也能避免出现空聚类的现象。显然，这种改进解决了K-均值聚类算法对随机初始化敏感的问题。

在改进方案的基础上，继续K-均值聚类算法步骤（2）、（3）、（4），可获得数据的聚类结果。将经过初始化改进后算法仍称为K-均值聚类算法。

3 聚类数量估计与聚类质量评价

经典K-均值聚类算法不能确保收敛到全局最优^［22］是由于人为指定的聚类数量与数据的聚类结构不相匹配所致。为此，本文估计聚类数量思路为：首先，在K可能取值范围［K _min， K _max］内，用每个K值作为参数运行一次K-均值算法，可获得一系列聚类结果；然后，选择这些结果中最优的SSE所对应的K值作为数据的潜在聚类数量。由此就涉及到两个问题：一是需要估计K的可能取值范围，二是构建合理的聚类性能指标对不同K值的聚类质量进行评价。

由于数据 X 的聚类数量K是有限的正整数，尽管具体K值无法事先得知，但可通过数据统计特性估计出其范围。当所有数据点都属于一个聚类时， X 的最小聚类数量为K _min=1；而聚类数量最大的情况是每个样本点形成一个单独聚类，即K _max=n。然而，实际数据本身的聚类数量一般满足K<<n，因此只要估计出K的可能最大值K _max，就可以构造出聚类数量范围［1， K _max］。

统计经验法则常用于对服从正态分布的数据结构进行推断，它表明几乎所有（约99.7%）的数据观测值都将落在以均值m为中心的3个标准差σ之内，即3-σ规则。

对于给定p维数据 X，其对应特征的均值 m _j 和标准差 σ _j （j=1， 2， …， p）一般都是有限值。考虑数据中所有的特征，则最大的聚类数量K _max与最小的K _min采用经验规则估计为

K m a x = r o u n d {m a x j ∈ [1, p] (m j + 3 σ j)}

（13）

K m i n = r o u n d {m i n j ∈ [1, p] (m j - 3 σ j)}

（14）

式中：round（）为取整函数。若利用PCA对数据进行压缩，形成只有q（q<<p）维的特征子空间，这时式（13）和（14）中j的取值范围就变为［1， q］。一般地，式（14）计算的结果可能为负值，因此在本文中默认K _min=1。

K-均值算法的优化目标是最小化SSE。在K的可能取值范围［1， K _max］中，由式（9）可知SSE失真的取值随着K值的变化而变化。当K值逐渐增加时，数据各样本点也逐渐接近于它们被指定的质心，使得SSE值逐渐下降。为此，只要识别出SSE开始快速增长所对应的K值即可得到数据的聚类数量，这就是著名的肘部法。

要判断由肘部法所估计的聚类数量是否与 X 本身的聚类结构相适应，就需要计算聚类的轮廓系数并进行轮廓分析^［23］，以实现对聚类质量的客观评价。聚类C_i 中数据点 x _i 的凝聚力a_i ^［24］为

a i = 1 n i - 1 ∑ x i, x j ∈ C i (j ≠ i) D (x i, x j)

（15）

式中：D（ x _i， x _j ）为欧氏距离；n_i 为C_i 中样本数量。若 x _i 是C_i 中唯一数据点，则a_i =0；否则a_i 是 x _i 到C_i 中其他样本点 x _j （j≠i）的平均距离。显然，a_i 值是度量同一聚类中数据点的相似程度。

聚类C_i 中样本点 x _i 到其他聚类C_k （k≠i）中数据点 x _j （设C_k 中数据点数为n_k ）的平均距离为

b i k = 1 n k ∑ x i ∈ C i, x j ∈ C k (k ≠ i) D (x i, x j)

（16）

基于b_ik，聚类C_i 的分离性b_i ^［24］为

b i = m i n k ∈ [1, K], k ≠ i b i k

（17）

式中：K为数据聚类数量；b_i 是聚类C_i 的数据点 x _i 到与它最邻近聚类C_k （k≠i）中所有数据样本点的平均距离。显然，b_i 值度量数据点 x _i 与其他聚类中数据点的相异程度。

一般地，b_i ≥a_i。对数据 X 中每个数据点 x _i，其对应的轮廓系数^［23］为

s i = b i - a i m a x {b i, a i}

（18）

式中：s_i 的取值范围为［0，1］。若b_i =a_i，则s_i =0，即两个不同聚类是难以区分的，这意味着聚类质量很差；若b_i >>a_i，则s_i ≈1，即不同集群的数据被明确地分离开，这说明聚类的质量高。

为进一步分析聚类的性能，定义数据 X 中所有样本的平均轮廓系数S为

S = 1 n ∑ i = 1 n s i

（19）

式中：S用于推断聚类质量。S越大，聚类质量越高，体现为不同聚类的轮廓系数具有大致相同的外观尺寸。

4 本文算法流程

在以上内容的基础上，归纳出本文方案所对应算法的流程与伪代码如下：

初始化改进与可视化确定聚类数量的 K-均值算法

输入：数据的维数（特征数量）p，样本容量N

输出：聚类数量K和质心向量 M =［ m ₁， m ₂，...， m _k ］基本流程

1.数据 X 的标准化预处理；2. If p≥8 go to 3， else go to 4；3.对标准化数据执行 PCA 降维的预处理，使数据维数压缩为q维；4.利用经验法则估计聚类数量范围［K _min，K _max］；5.用肘部法在［K _min，K _max］中搜索最佳 SSE 对应的聚类数量 K；6.采用最远质心选择和最小-最大距离规则改进经典K-均值算法的随机初始化；7.将K值作为输入参数运行改进的K-均值算法获得聚类结果；8.计算聚类的轮廓系数，利用轮廓分析评价聚类质量；9.确定与数据本身相适应最优聚类数量K；10.返回聚类数量K以及对应的质心向量 M。

5 仿真及结果分析

为验证本文方案的性能，利用不同类型的数据集作仿真，所有试验均在Spyder 5上执行。

5.1 聚类性能度量指标

对于聚类结果的评价，除上述的轮廓系数之外，还有一些常用的聚类质量评价指标，例如兰德指标、互信息分数、同质性（完备性）及其V-测度、Fowlkes-Mallows指标、Calinski-Harabasz指标及Davies-Bouldin指标等。

对于只有两个聚类的数据集，兰德指标^［25］定义为

R I = a + b C 2 N

（20）

式中：a为在真实标签中处于同一簇中的样本对个数；b为真实簇和算法预测簇中处于不同簇的样本对个数；N为样本容量；分母表示数据集中数据对的总数。

如果数据被分成多于两个簇，则需要采用调整的兰德分数^［26］

A R I = R I - E [R I] m a x (R I) - E [R I]

（21）

式中：E［∙］表示数学期望。

U和V之间的互信息分数^［27］定义为

M I (U, V) = ∑ i = 1 | U | ∑ j = 1 | V | P (i, j) l g P (i, j) P (i) P' (j)

（22）

式中： U和V分别为对N个数据样本分配的标签； P（i）=|U_i |/N和P'（j）=|V_j |/N分别为从U和V中随机挑选的数据点落入聚类U_i 和V_j 的概率。调整互信息和归一化的互信息分别为

A M I = M I - E [M I] m e a n [H (U), H (V)] - E [M I]

（23）

N M I (U, V) = M I (U, V) m e a n [H (U), H (V)]

（24）

式中：mean［∙］是熵的广义均值。AMI和NMI具有更强的鲁棒性^［28］。

同质性指标和完备性指标分别为

H I = 1 - H (C | K) H (C)

（25）

C I = 1 - H (K | C) H (K)

（26）

式中： H（C|K）和H（K|C）分别为给定簇分配的类（class）的条件熵；H（C）为类的熵；H（K）为簇的熵。

V-测度^［29］是一种综合考虑同质性和完备性的评估指标，公式为

V M = 2 H I ⋅ C I H I + C I

（27）

Fowlkes-Mallows指标^［30］定义为成对精度和召回率的几何平均值，公式为

F M I = T P (T P + F P) (T P + F N)

（28）

式中： TP为真标签和预测标签中属于相同簇的点对的数量；FP为属于真实标签中的同一簇而不属于预测标签中的点对数量；FN为属于预测标签中的同一簇而不属于真实标签中的点对数量。

以上指标中，RI、ARI、MI、AMI、NMI、HI、CI、VM、FMI的取值均在［0，1］范围内。其指标值越接近1则聚类质量越高，而越接近于0则聚类质量越差。

Davies-Bouldin指标^［31-32］用于度量集群内的紧密度和聚类间的分离度

D B = 1 K ∑ i = 1 K m a x i ≠ j R i j

（29）

式中：K为聚类数量；R_ij 为

R i j = s i + s j d i j

（30）

式中： s_i 和s_j 分别为聚类i和聚类j的每个点与它们的聚类质心之间的平均距离，也称为聚类直径；d_ij 为聚类质心i和j之间的距离。与以上其他指标相反，DB的值越小，聚类结果越好。

Calinski-Harabasz指标^［33］也称为方差比标准，如式（31）所示。

C H I = t r (B k) t r (W k) · N X - K K - 1

（31）

式中： N _X 为数据 X 样本容量；K为聚类数量；tr（B_k ）为聚类间协方差矩阵的迹；tr（W_k ）为集群内协方差矩阵的迹。CHI值不受范围［0，1］的限制。一般地，CHI值越大，聚类结果越好。

5.2 二维随机数据集

在对聚类算法的测试中，经常使用随机数据验证算法性能。为了可视化的目的，这里仅采用二维的随机数据集进行试验分析。

随机产生的二维Blob数据集是由900个样本点形成的6个自然集群。横轴是特征1，纵轴是特征2。两个特征的均值分别为m ₁=2.541，m ₂=2.367；而标准差为：σ ₁=3.874， σ ₂=3.239。该数据的散点图如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 数据集Blob的散点图

对K-均值算法的主要参数设置如下：指定聚类数量为K=6，最大迭代次数为300。在实际应用中，若算法在最大迭代次数到来之前已经收敛，则迭代过程停止。然而，当最大迭代次数到来时，算法可能仍不收敛，若要增加迭代次数，则计算成本增加。为此，本文附加一个误差容限参数来控制收敛条件。在以下的仿真中，均采用容限值tol=10^-4。

K-均值聚类算法对Blob数据集的聚类及对聚类质心的辨识结果如图2所示。

显示原图|下载原图ZIP|生成PPT

图2 在给定 K=6时Blob数据的聚类结果和轮廓图

从图2可看出，6个聚类的质心被放置在自然形成数据堆的中心点。这说明，当指定K=6时算法的聚类结果与数据Blob的原始划分是完全一致的。

从图2还看出，尽管各轮廓系数并不完全相同，但这6个聚类的轮廓外观相互之间还是比较协调的。另外，在图2中，Blob数据中所有样本的平均轮廓系数（粗虚线）S值约为0.75，它接近1而远离0；意味着算法的聚类质量较高。

实际上，数据集 X 固有的聚类数量K一般是未知的，因而需要估计它的范围。将Blob数据集两个特征的均值和标准差分别代入式（13），则得到K _max=11，即［K _min， K _max］=［1， 11］。为便于观察，这里仅绘制出变化范围K∈［2， 11］所对应的SSE曲线，其结果如图3所示。

显示原图|下载原图ZIP|生成PPT

图3 Blob数据集SSE随 K 值变化曲线

从图3可看出，在K<6时， SSE随K值的变化较剧烈，而当K>6时，SSE随K值变化平缓，即SSE曲线的肘部位于K=6的位置。即数据最优聚类数量为K ₀=6，这与Blob数据集是完全吻合的。相反地，若指定的聚类数量K偏离SSE曲线的肘部位置，其结果用如下仿真来说明。

若设置参数K=5，则K-均值的聚类结果如图4所示。从图中可知，算法将原本两个集群的数据强制地合并成图中圆线框起来的聚类4。该结果与数据Blob固有的聚类结构相悖。

显示原图|下载原图ZIP|生成PPT

图4 在给定 K=5时Blob数据集的聚类结果和轮廓图

从图4还看出，聚类1、2、3、5是数据集Blob的固有集群，它们的轮廓外观较协调，而由算法产生新聚类4的轮廓发生明显扭曲。而全部数据的平均轮廓系数S≈0.68，与图2b中的0.75相比较，减少了近10%。说明在给定参数K=5时，算法的聚类质量下降了。

同样地，若设置K=7时，其聚类结果如图5所示。

显示原图|下载原图ZIP|生成PPT

图5 在给定 K=7时Blob数据集的聚类结果和轮廓图

从图5看出，由圆圈框起来的那堆数据被强行地分裂为两个聚类1和7，其对应的质心相距太近，这和数据本身的聚类结构不相符。

从图5还看出，聚类2、3、4、5、6分别对应于数据集Blob本身的集群，而集群1和7的轮廓尺寸明显小于其他的轮廓，这表明集群1和7形成单独的聚类是不合理的；并且在图5中，平均的轮廓系数也降低为S≈0.67，表示聚类质量的下降。

将K=5、6、7时K-均值聚类算法对Blob数据产生的聚类性能指标计算出来，如表1所示。

表1 参数 K=5、6、7时Blob数据的聚类性能

K	ARI	AMI	NMI	HI	CI	VM	FMI	DB	CHI
5	0.822 72	0.930 62	0.931 08	0.871 05	1.000 0	0.931 08	0.865 30	0.457 98	4 652.708 27
6	1.000 0	1.000 0	1.000 0	1.000 0	1.000 0	1.000 00	1.000 00	0.347 11	9 420.726 63
7	0.949 35	0.969 05	0.969 33	1.000 0	0.940 49	0.969 33	0.958 26	0.560 21	8 404.354 59

从表1可看出，当K=6时，算法的聚类性能明显要比K=5和K=7的性能提高很多。而K=7却比K=5对应的性能高，这是因为聚类数量越多，数据点越接近其被指定的聚类质心。

通过以上对Blob数据集的仿真可知，对于K-均值聚类算法，无论对算法输入参数（聚类数量）K过高或过低，都将会对聚类结果产生影响，造成算法产生的聚类质量恶化。

5.3 高维的实际数据集

美国加州大学欧文分校机器学习数据库包含大量真实数据集，其中的红酒数据集是高维数据。它是对3种不同种类葡萄酒进行化学分析所得出的13种不同成分含量的数据。所谓不同成分就是数据的不同特征，它们分别表示为x ₁， x ₂， …， x ₁₃。红酒数据集共包含178个样本，3种葡萄酒的样本数分别为59、71、48。为简单起见，将3种葡萄酒的类标签分别表示为1、2、3。对于所有178个样本，计算出它们每个特征的均值m和标准差σ，其结果如表2所示。

表2 红酒数据集13个特征的均值与标准差

x	x ₁	x ₂	x ₃	x ₄	x ₄	x ₆	x ₇	x ₈	x ₉	x ₁₀	x ₁₁	x ₁₂	x ₁₃
m	13.0	2.34	2.37	19.5	99.7	2.3	2.0	0.36	1.59	5.06	0.96	2.61	746.89
σ	0.81	1.12	0.27	3.34	14.3	0.63	1.0	0.12	0.57	2.32	0.23	0.71	314.91

从表2可以看出，特征x ₈和特征x ₁₃的均值相差2 075倍，标准差相差2 624倍，并且各个特征的度量单位也是不相同的。

为便于聚类分析，首先对红酒数据标准化，使其服从正态分布，并计算其协方差矩阵，然后将该矩阵分解为特征值和特征向量。把特征值按降序排列，其结果如表3所示。

表3 降序排列的13个特征值

λ ₁	λ ₂	λ ₃	λ ₄	λ ₅	λ ₆	λ ₇	λ ₈	λ ₉	λ ₁₀	λ ₁₁	λ ₁₂	λ ₁₃
4.732	2.511	1.454	0.924	0.858	0.645	0.551	0.351	0.291	0.252	0.227	0.177	0.104

用表3中的数据可计算出每个特征的方差解释率R_k （k=1，2，…，13）。由R_k 定义可知，所有特征的R_k 值累加起来的和为1，即R_k 是各个特征在数据的聚类分析中所包含信息的百分比。为观察各主分量对聚类分析的贡献率，将13个方差解释率按照从大到小的次序绘制出来，其结果如图6所示。

显示原图|下载原图ZIP|生成PPT

图6 红酒数据集13个特征的方差解释率

在图6中，还用阶梯线绘出了各个主分量方差解释率的累计值。从图6中也可以看出，第1个主分量大约占了整个解释方差的40%，而第1、第2主分量大约累计所占的比例几乎达到了60%。因此，仅提取前两个主分量构成2维的特征子空间以实现数据的降维。

在选择出前两个主分量后，将它们堆叠起来可得到13×2维的投影矩阵 W；其中 W 的第1、第2列即为第1、第2个主分量。对原始的13维数据矩阵 X 进行变换得 X _sub= XW。

将压缩后的数据集 X _sub在二维子空间上的散点图绘制出来，如图7所示。

显示原图|下载原图ZIP|生成PPT

图7 数据集 X _sub 在二维子空间的散点图

在图7中，用小圆圈标识了3类数据之间互有交叉的样本点。这是由于仅从13个特征中抽取了2个最重要的特征，未能将数据的全部信息利用，因而形成的聚类之间数据点互有渗透。尽管如此， 3个聚类的数据基本上是满足可分离的。

根据所选定的前两个主成分所对应的特征，将前两个特征的均值和标准差分别代入式（13）中计算可得K _max=7，即 X _sub的聚类数量范围K∈［1， 7］。在此范围内，绘制出失真SSE随K值变化的曲线如图8所示。

显示原图|下载原图ZIP|生成PPT

图8 X _sub 数据集SSE随K值变化曲线

从图8可看出，不能确定失真曲线的肘部是位于K=3还是K=4。为此将K=3、K=4作为K-均值算法的输入参数。

当指定聚类数量K=3时，数据 X _sub的聚类结果及对应的轮廓系数如图9所示。从图9可看出，数据集 X _sub的3个聚类质心被准确地定位在每堆经降维后的数据中心。从图中还可看出，3个聚类的轮廓系数略有差别，这是由3种葡萄酒的样本数量并不平衡（不相等）导致的。但从整体看，这3个聚类的轮廓系数基本上是一致的；并且所有178个样本数据的平均轮廓系数S≈0.67，说明经过PCA处理后形成的低维数据的聚类质量是比较高的。

显示原图|下载原图ZIP|生成PPT

图9 在给定K =3时数据 X _sub 的聚类结果和轮廓图

当指定聚类数量为K=4时，聚类结果如图10所示。

显示原图|下载原图ZIP|生成PPT

图10 在给定K =4时数据 X _sub 的聚类结果和轮廓图

从图10可看出，聚类1和聚类3对应于 X _sub原本的集群，而聚类2、4的轮廓尺寸都明显发生了扭曲。算法所产生的聚类4是因为指定的参数K不合理而形成的。此外，平均轮廓系数降低为S≈0.575，与图9中的值0.67相比，下降了接近10%，表明算法的聚类质量恶化。

为了更精确地分析K=3和K=4的聚类效果，计算这两种情况下聚类的性能指标，其结果如表4所示。

表4 参数 K=3、4时 X _sub 数据集的聚类性能指标

K	ARI	AMI	NMI	HI	CI	VM	FMI	DB	CHI
3	0.895 06	0.880 81	0.882 07	0.883 98	0.880 16	0.882 07	0.930 36	0.597 27	344.792 59
4	0.677 39	0.722 50	0.726 39	0.822 65	0.650 29	0.726 39	0.778 85	0.742 23	328.515 50

从表4可看出，当K=3（真实聚类数量）时，K-均值算法的各项聚类性能指标都要高于K=4的情况。另外，比较表1和表4的数据可知，在同等情况下，算法对经过PCA降维后数据的聚类质量要低于算法对原始数据的聚类质量，这是由于数据压缩后造成了一定的信息损失所致。

5.4 不同算法效果的比较

为了对比本文方案与其他K-均值改进方法的性能，采用UCI的多个真实数据集进行测试，其选择的数据集的主要信息如表5所示。

表5 UCI数据集的主要信息

数据集名称	维数	样本容量	聚类数量
Adult	14	32 561	2
Iris	4	150	3
Seeds	7	210	3
Abalone	8	4 177	3
Car Evaluation（Car）	6	1 728	4
Dermatology（Derm）	34	366	4
Glass	9	214	7

从表5可知，数据集的聚类数量是已知的。尽管如此，不同的方法仍可能产生不一样的结果，这是由于各种方法依赖于本身的参数设置，且由于对数据中噪声敏感程度不同造成的。为此，以下算法将采用最基本配置进行仿真。

5.4.1 初始聚类质心的选择

为评价不同方法初始质心选择的性能，采用误差百分比和Wilks的α检验统计量。误差百分比^［11］计算如式（32）所示。

e r r = ε N × 100

（32）

式中：ε为数据集中被错误分类的样本数量；N为数据集中样本的总数。

Wilks的α检验统计量^［11］如式（33）所示。

α = | W | | W + B |

（33）

式中： W 为处在平方和与乘积矩阵^［11］之内； W + B 为总的平方和与乘积矩阵。α值越小，说明不同聚类间差异越显著。

将本文的最远质心选择及最小-最大距离规则与文献［11］~［14］的方法分别应用于上述的7个UCI数据集，获得对应的聚类性能指标如表6和表7所示。

表6 不同方法的误差百分比 (%)

数据集	误差
数据集	文［11］	文［12］	文［13］	文［14］	本文
Adult	12.31	9.8	11.2	8.8	0
Iris	10.7	8.12	9.43	7.43	2.2
Seeds	5.4	6.32	8.63	7.56	3.3
Abalone	7.9	9.32	10.3	12.2	5.2
Car	36.4	25.5	31.3	21.3	11
Derm	12.4	15.3	11.2	16.4	7.2
Glass	11.3	18.6	15.3	14.2	6.4

表7 不同方法的 α 检验统计量

数据集	α
数据集	文［11］	文［12］	文［13］	文［14］	本文
Adult	0.1	0.05	0.1	0.08	0.02
Iris	0.03	0.06	0.07	0.06	0.003
Seeds	0.09	0.1	0.1	0.1	0.05
Abalone	0.1	0.1	0.1	0.11	0.09
Car	0.41	0.3	0.33	0.34	0.11
Derm	0.05	0.07	0.06	0.08	0.03
Glass	0.1	0.2	0.11	0.1	0.04

从表6、表7可知，对于不同的数据集，各种算法的聚类性能是不相同的。尽管如此，本文方案对每一种数据集的聚类性能都明显优于其他方法。

5.4.2 聚类数量的确定

首先对UCI数据进行标准化；然后对维数p≥8的数据集采用PCA作压缩预处理；在此基础上，利用统计经验法则估计出每个数据集聚类数量K取值范围［1， K _max］。在此范围内，分别应用本文方案及文献［15］~［19］的方法，估计不同数据集的最优聚类数量，其结果如表8所示。

表8 不同方法所估计的最优聚类数量

数据集	α值
数据集	文［15］	文［16］	文［17］	文［18］	文［19］	本文
Adult	2	2	2	2	2	2
Iris	2 or 3	3	3 or 4	3	2 or 3	3
Seeds	3	2 or 3	3	2 or3	3	3
Abalone	2 or 3	3	3	3 or 4	3	3
Car	4	3 or 4	4 or 5	3 or 4	3 or 4	4
Derm	3 or 4	4 or 5	4	3 or 4	4 or 5	4
Glass	6 or 7	7	7 or 8	7	7	7

从表8可看出，一些方法提供的聚类数量并不是完全唯一的，而是两个数字。这是因为基于各种算法中的测量指标，在搜索与最佳指标相对应的聚类数量时存在一些模糊性，即其最佳指标处于两个数字之间。然而，在表8中本文方案对每种数据集都提供了确定的、唯一的最优聚类数量，并且与数据本身固有的聚类结构相一致。这是由于本文方案利用肘部法估计出聚类数量后，再通过轮廓分析法排除与真实聚类结构不适应的选项，从而保证给出最合理的聚类数量。

6 结论

为解决经典K-均值算法存在的缺陷，本文作了相关研究。其主要贡献体现在以下方面：

（1）对经典K-均值算法采用初始化的改进措施，确保算法不出现空聚类，且具有合理的初始划分；

（2）对高维数据集，利用主分量分析抽取数据集中最重要的少量特征以实现数据压缩；

（3）利用统计经验法则估计数据的可能聚类数量范围，在此基础上，用肘部法搜寻数据集固有的聚类数量；

（4）通过计算不同聚类的轮廓系数，利用轮廓分析法直观地评估算法的聚类质量，从而验证聚类数量选择的正确性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	Grolemund G， Wickham H.A cognitive interpretation of data analysis［J］.International Statistical Review，2014，82（2）：184-204.

2	Wang R L， Ji W T， Liu M Z，et al.Review on mi-ning data from multiple data sources［J］.Pattern Recognition Letters，2018，109：120-128.

3	Clancy T C， Khawar A， Newman T R.Robust signal classification using unsupervised learning［J］．IEEE Transactions on Wireless Communications，2011，10（4）：1289-1299．

4	Xiao Q G， Li C B， Tang Y，et al.Energy efficiency modeling for configuration-dependent machining via machine learning：a comparative study［J］.IEEE Transactions on Automation Science and Engineering，2021，18（2）：717-730.

5	Caruso G， Gattone S A， Fortuna F，et al.Cluster analysis for mixed data：an application to credit risk evaluation［J］.Socio-Economic Planning Sciences，2021，73：100850.

6	Huang D， Wang C D， Peng H X，et al.Enhanced ensemble clustering via fast propagation of cluster-wise similarities［J］.IEEE Transactions on Systems，Man，and Cybernetics：Systems，2021，51（1）：508-520.

7	Ikotun A M， Ezugwu A E， Abualigah L，et al.K-means clustering algorithms：a comprehensive review variants analysis，and advances in the era of big data［J］.Information Sciences：an International Journal，2023，622（1）：178-210.

8	Biswas T K， Giri K， Roy S.ECKM：an improved k-means clustering based on computational geo-metry［J］.Expert Systems with Applications，2023，212：118862.

9	Steinley D.K-means clustering：a half-century synthesis［J］.The British Journal of Mathematical and Statistical Psychology，2006，59（1）：1-34.

10	Steinley D.Stability analysis in K-means clustering［J］.The British Journal of Mathematical and Statistical Psychology，2008，61（2）：255-273.

11	Erisoglu M， Calis N， Sakallioglu S.A new algorithm for initial cluster centers in k-means algorithm［J］.Pattern Recognition Letters，2011，32（14）：1701-1705.

12	Khan F.An initial seed selection algorithm for k-means clustering of georeferenced data to improve replicability of cluster assignments for mapping application［J］.Applied Soft Computing，2012，12（11）：3698-3700.

13	Kumar K M， Reddy A M.An efficient k-means clustering filtering algorithm using density based initial cluster centers［J］.Information Sciences：an International Journal，2017，418（1）：286-301.

14	Ahmad A， Khan S S.InitKmix-a novel initial partition generation algorithm for clustering mixed data using k-means-based clustering［J］.Expert Systems with Applications，2021，167：114149.

15	Karim A， Loqman C， Boumhidi J.Determining the number of clusters using neural network and max stable set problem［J］.Procedia Computer Science，2018，127（1）：16-25.

16	Viloria A， Lezama O B P.Improvements for determining the number of clusters in k-means for innovation databases in SMEs［J］.Procedia Computer Science，2019，151（1）：1201-1206.

17	Abdalameer A K， Alswaitti M， Alsudani A A，et al.A new validity clustering index-based on finding new centroid positions using the mean of clustered data to determine the optimum number of clusters［J］.Expert Systems with Applications，2022，191：116329.

18	Kariyam，Abdurakhman， Effendie A R.A medoid-based deviation ratio index to determine the number of clusters in a dataset［J］.MethodsX，2023，10：102084.

19	Lippiello E， Baccari S， Bountzis P.Determining the number of clusters，before finding clusters，from the susceptibility of the similarity matrix［J］.Physica a Statistical Mechanics and Its Applications，2023，616：128592.

20	Lee G， Sim E， Yoon Y，et al.Probabilistic orthogonal-signal-corrected principal component analysis［J］.Knowledge-Based Systems，2023，268：110473.

21	Kwak N.Principal component analysis based on L1-norm maximization［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2008，30（9）：1672-1680.

22	Selim S Z， Ismail M A.K-means-type algorithms：a generalized convergence theorem and characte-rization of local optimality［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6（1）：81-87.

23	Bagirov A M， Aliguliyev R M， Sultanova N.Fin-ding compact and well-separated clusters：clustering using silhouette coefficients［J］.Pattern Recognition，2023，135：109144.

24	Batool F， Hennig C.Clustering with the average silhouette width［J］.Computational Statistics & Data Analysis，2021，158：107190.

25	Hubert L， Arabie P.Comparing partitions［J］.Journal of Classification，1985，2（1）：193-218.

26	Steinley D.Properties of the hubert-arabie adjusted rand index［J］.Psychological Methods，2004，9（3）：386-396.

27	Strehl A， Ghosh J.Cluster ensembles-a knowledge reuse framework for combining multiple partitions［J］.Journal of Machine Learning Research，2003，3（3）：583-617.

28	Yang Z， Algesheimer R， Tessone C J.A comparative analysis of community detection algorithms on artificial networks［J］.Scientific Reports，2016，6：30750.

29	Rosenberg A， Hirschberg J.V-measure：a conditional entropy-based external cluster evaluation measure［J］.EMNLP-CoNLL 2007-Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning，2007，10：410-420.

30	Fowlkes E B， Mallows C L.A method for compa-ring two hierarchical clusterings［J］.Journal of the American Statistical Association，1983，78（383）：553-569.

31	Davies D L， Bouldin D W.A cluster separation measure［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1979，1（2）：224-227.

32	Halkidi M， Batistakis Y， Vazirgiannis M.On clustering validation techniques［J］.Journal of Intelligent Information Systems，2001，17（2）：107-145.

33	Calinski T， Harabasz J.A dendrite method for cluster analysis［J］.Communications in Statistics - Theory and Methods，1974，3（1）：780133830.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 特征缩放与主分量提取

2 K -均值聚类算法的初始化改进

3 聚类数量估计与聚类质量评价

4 本文算法流程

5 仿真及结果分析

5.1 聚类性能度量指标

5.2 二维随机数据集

图1 数据集Blob的散点图

图2 在给定 K=6时Blob数据的聚类结果和轮廓图

图3 Blob数据集SSE随 K 值变化曲线

图4 在给定 K=5时Blob数据集的聚类结果和轮廓图

图5 在给定 K=7时Blob数据集的聚类结果和轮廓图

表1 参数 K=5、6、7时Blob数据的聚类性能

5.3 高维的实际数据集

表2 红酒数据集13个特征的均值与标准差

表3 降序排列的13个特征值

图6 红酒数据集13个特征的方差解释率

图7 数据集 X sub 在二维子空间的散点图

图8 X sub 数据集SSE随K值变化曲线

图9 在给定K =3时数据 X sub 的聚类结果和轮廓图

图10 在给定K =4时数据 X sub 的聚类结果和轮廓图

表4 参数 K=3、4时 X sub 数据集的聚类性能指标

5.4 不同算法效果的比较

表5 UCI数据集的主要信息

5.4.1 初始聚类质心的选择

表6 不同方法的误差百分比 (%)

表7 不同方法的 α 检验统计量

5.4.2 聚类数量的确定

表8 不同方法所估计的最优聚类数量

6 结论

参考文献

图7 数据集 X _sub 在二维子空间的散点图

图8 X _sub 数据集SSE随K值变化曲线

图9 在给定K =3时数据 X _sub 的聚类结果和轮廓图

图10 在给定K =4时数据 X _sub 的聚类结果和轮廓图

表4 参数 K=3、4时 X _sub 数据集的聚类性能指标