基于改进剩余强度模型的复合材料疲劳寿命预测

赵维涛; 孟庆辉

doi:10.3969/j.issn.2095-1248.2024.03.001

沈阳航空航天大学学报 >

2024 , Vol. 41 >Issue 3: 1 - 6

DOI: https://doi.org/10.3969/j.issn.2095-1248.2024.03.001

航空宇航工程

基于改进剩余强度模型的复合材料疲劳寿命预测

赵维涛 ,
孟庆辉

展开

沈阳航空航天大学航空宇航学院，沈阳 110136

赵维涛(1977-),男,辽宁沈阳人,教授,博士,主要研究方向:结构可靠性,E-mail:zhwt201@126.com。

收稿日期: 2024-01-17

网络出版日期: 2024-08-30

基金资助

国家自然科学基金(12272240)

收起

Fatigue life prediction of composite materials based on improved residual strength model

Weitao ZHAO ,
Qinghui MENG

Expand

College of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2024-01-17

Online published: 2024-08-30

Fold

摘要

复合材料强度退化规律对研究结构疲劳寿命具有重要意义，然而现有剩余强度模型均需利用剩余强度试验数据确认模型参数，模型构建成本较高。通过探究复合材料疲劳寿命和剩余强度的关系，以疲劳寿命累积分布函数为出发点，构建具有明确物理意义的损伤度，进而提出改进剩余强度模型。改进剩余强度模型不需要剩余强度试验数据，仅需初始静强度和疲劳寿命数据。在改进剩余强度模型基础上，构建S-N-φ疲劳寿命预测模型，该模型可以考虑初始静强度对疲劳寿命的影响。算例结果表明，改进剩余强度模型的预测精度是满意的，S-N-φ模型相比经典S-N曲线模型具有更好的预测精度。

关键词： 复合材料; 剩余强度; 疲劳寿命; S-N曲线; 损伤度

本文引用格式

赵维涛 , 孟庆辉 . 基于改进剩余强度模型的复合材料疲劳寿命预测[J]. 沈阳航空航天大学学报, 2024 , 41(3) : 1 -6 . DOI: 10.3969/j.issn.2095-1248.2024.03.001

Abstract

The strength degradation law of composite materials is very important for studying the structural fatigue life. However， some parameters involved in existing residual strength models are confirmed using residual strength test data， so the cost of model construction is high. By exploring the relationship between fatigue life and residual strength of composite materials， taking the cumulative distribution function of fatigue life as the starting point， a damage degree with clear physical meaning was constructed，and then an improved residual strength model was proposed. The improved residual strength model didn’t need residual strength test data but only initial static strength and fatigue life data. A fatigue life prediction model called S-N-φ model was constructed based on the improved residual strength model， which can consider the influence of initial static strength on fatigue life. The results show that the prediction accuracy of the improved residual strength model is satisfactory， and the S-N-φ model has better prediction accuracy than the classical S-N curve model.

Key words： composite materials; residual strength; fatigue life; S-N curve; damage degree

复合材料具有与金属材料不同的力学属性，其疲劳损伤机制与金属材料亦有所不同。宏观上，复合材料疲劳损伤可利用强度退化程度进行度量。近年来，人们在利用剩余强度表征复合材料疲劳损伤方面进行了大量的研究。

Schaff等^［1］基于强度退化提出了疲劳损伤模型，用于预测复合材料在恒幅应力水平下的剩余强度和疲劳寿命。Wu等^［2］基于刚度退化提出了疲劳损伤模型来描述复合材料的损伤演化规律。Huston^［3］提出了一种较为简单的模型来描述复合材料疲劳行为，该模型仅包含最大施加应力、静强度、失效循环次数和一个常数。Wu等^［4］研究了复合材料静强度和疲劳寿命分散的原因，发现复合材料层合板制造过程中的原始缺陷是造成静强度和疲劳寿命离散的主要原因。俞耀等^［5］基于渐进损伤原理构建了疲劳寿命预测模型，该模型考虑了纤维强度的离散性。徐蓉霞等^［6］基于灰色系统，提出了单向层合板疲劳寿命模型和损伤函数，与最小二乘法相比，提高了拟合精度。赵晟等^［7］假设累积损伤与应力呈线性关系，提出了基于剩余强度的归一化衍生疲劳损伤模型。Montesano等^［8］提出了疲劳预测模型，该模型可用于评估聚合物基复合材料结构的损伤容限能力。Kang等^［9］将累积损伤定义为弹性模量的函数，建立了基于概率损伤累积行为的疲劳寿命概率模型。Kassapoglou等^［10］对基于循环失效概率的复合材料层合板疲劳模型进行了改进，改进后在模型计算时仅需材料静强度值和相关试验散点。拓宏亮等^［11］将最大应力失效准则和Puck静力失效准则作为疲劳失效准则，建立了复合材料层合板的疲劳损伤模型。李嘉骞等^［12］基于等效静强度模型和可靠性理论，推导出复合材料疲劳寿命形状参数和剩余强度形状参数之间的函数关系。Yao等^［13］基于层合板损伤状态可用瞬时剩余强度表示的假设，提出了基于剩余强度的累积疲劳损伤模型。Kassapoglou^［14］基于失效周期是任意给定周期内失效概率函数的假设，提出了确定复合材料结构在恒幅载荷作用下疲劳寿命曲线的方法。Mao等^［15］提出了通用损伤累积模型来描述复合材料的退化，损伤函数能够很好地模拟试验结果。杨成鹏等^［16］综述了疲劳损伤演化的曲线模型、剩余刚度模型、剩余强度模型、疲劳模量模型和S-N曲线模型的研究进展，并就疲劳研究的不足进行了综合阐述。

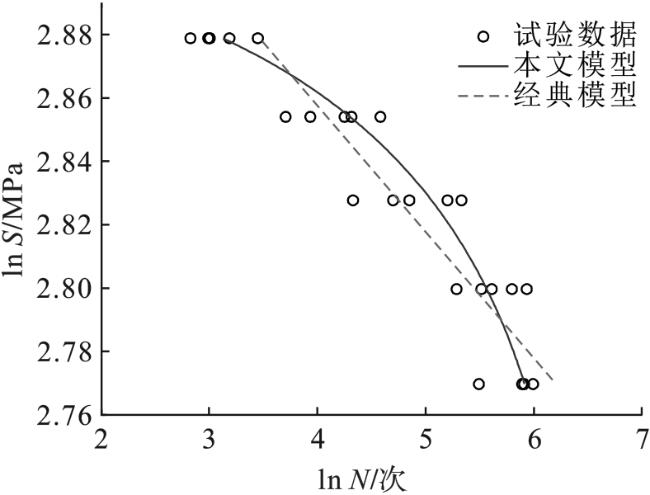
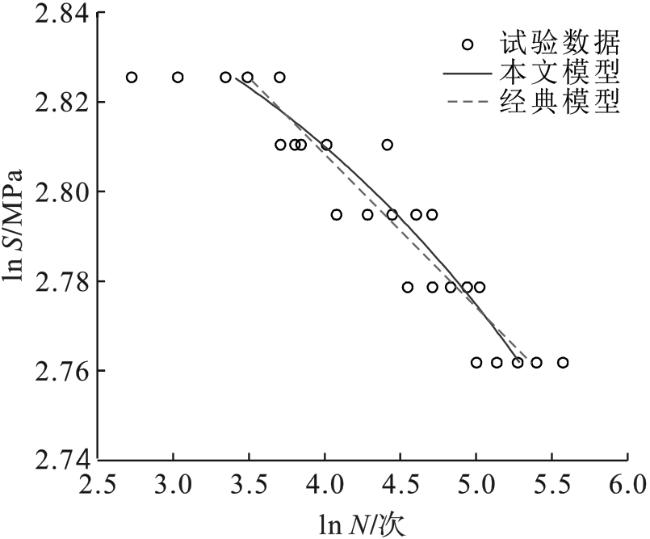
综上，人们在剩余强度方面做了大量研究工作，建立了多种剩余强度模型。但已有模型应用的前提是需要利用剩余强度试验数据确认模型中的相关参数，然而剩余强度试验成本较高，且在实际工程中往往没有历史可用数据，这严重制约了已有模型的应用。因此，本文通过探讨复合材料损伤度与疲劳寿命和剩余强度的关系，构建具有明确物理意义的损伤度，提出改进剩余强度模型。在改进剩余强度模型基础上，建立S-N-φ疲劳寿命预测模型。利用初始静强度和疲劳试验数据，通过S-N-φ模型确认改进剩余强度模型中的参数。

1 剩余强度模型

1.1 经典剩余强度模型

复合材料强度退化规律已被广泛研究，研究表明，复合材料的强度退化具有以下3点特征^［13］：（1）在疲劳寿命初期，剩余强度下降较快；（2）在疲劳寿命中期，剩余强度下降速度适中且均匀；（3）在接近完全失效时，剩余强度下降非常迅速，当剩余强度等于最大应力时表现为“猝死”行为，疲劳失效发生。

基于复合材料强度退化特征，Schaff等^［1］提出的强度退化模型为

R (n) = R 0 - R 0 - S D (n)

（1）

D (n) = n / N c

（2）

式中：

R (n)

为剩余强度；

R 0

为初始强度（即静强度）；

S

为应力水平；

D (n)

为损伤度；

n

为循环次数；

N

为疲劳寿命；

c

为模型参数。

当式（2）中的参数

c

确定后，从数学角度来看，

n / N c

难以准确描述在整个寿命期内强度退化的3点特征。

Gao等^［17］提出的剩余强度模型为

R (n) = R 0 - R 0 - S D (n)

（3）

D (n) = s i n (a λ) c o s b s i n a c o s (b λ a)

（4）

式中：

λ = n / N

，为循环比；

a

和

b

是模型的两个参数。

1.2 改进剩余强度模型

通过式（2）和式（4）可以看出，损伤度的定义是根据复合材料强度退化特征采用猜想的函数形式，然后通过试验数据拟合模型参数，物理意义不明确。因此，文中构建物理意义明确的损伤度，进而建立改进剩余强度模型。

大量研究表明^{［2，4，6］}，复合材料的疲劳寿命服从两参数威布尔分布，疲劳寿命累积分布函数为

F N (n) = 1 - e x p - n β α

（5）

式中：

F N (n)

为疲劳寿命累积分布函数；

α

和

β

分别为形状参数和尺度参数。

形状参数

α

和尺度参数

β

可通过试验数据拟合得到，亦可以通过以下的经验公式^［18］确定。

α = V a r (N) E (N) - 1.086

（6）

β = E (N) Γ 1 + 1 / α

（7）

式中：

V a r (N)

为疲劳寿命的方差；

E (N)

为疲劳寿命的均值；

Γ (⋅)

为Gamma函数。

在任意载荷循环次数下，疲劳寿命累积分布函数的值表示寿命小于循环次数的概率，即疲劳失效概率。从强度角度来看，剩余强度等于最大施加应力时发生疲劳失效。因此，本文以疲劳寿命的累积分布函数为基础，构建损伤度，损伤度

D L (n)

的表达式为

D L (n) = n N d F N (n) F N (N)

（8）

式中：

d

为模型参数。

从式（8）可以看出，本文构建的损伤度能够满足“未加载时

D L (0) = 0

和疲劳失效时

D L (N) = 1

”的边界条件。式（8）从失效概率角度出发，引入了疲劳寿命累积分布函数，进而能够较准确地描述在整个寿命期内的强度退化特征。损伤度

D L (n)

的物理意义明确，即强度衰减量与疲劳寿命累积分布函数一一对应。

基于损伤度

D L (n)

，改进剩余强度模型为

R (n) = R 0 - R 0 - S D L (n)

（9）

2 S-N-φ疲劳寿命预测模型

在利用剩余强度模型对剩余强度预测之前，首先需要确认剩余强度模型中的相关参数。理想的方法是利用剩余强度试验数据拟合相关参数，然而剩余强度试验数据是难以获得的，即便能够获得也要付出高昂的成本。为解决此问题，结合经典S-N曲线思想，在改进剩余强度模型的基础上，建立同时考虑初始静强度和应力水平的疲劳寿命预测模型。利用初始静强度和疲劳寿命数据确认改进剩余强度模型式（9）中的参数

d

，进而达到不利用剩余强度试验数据仍可进行剩余强度预测的目的。

经典的S-N曲线模型可以表示为

N k 1 S k 2 = 1

（10）

式中：

k 1

和

k 2

为模型的两个参数。

由式（10）可知

1 / N = k 1 S k 2

，即疲劳寿命可以表示成应力水平

S

的函数。另外，应力水平

S

可以用初始强度

R 0

乘以某个系数表示，即

R 0 - S

可以转换为

R 0

与某个系数乘积的形式。基于以上思想将式（9）中的

R 0 - S n / N d

进行转换，得

R 0 - S n / N d = R 0 k 3 S k 4 n d

（11）

式中：

k 3

和

k 4

为模型参数。

由式（11）可得S-N-φ疲劳寿命预测模型为

N k 3 S k 4 = R 0 - S R 0 1 / d = φ 1 / d

（12）

式中，参数

φ

的表达式为

φ = (R 0 - S) / R 0

（13）

从式（10）和式（12）可以看出，S-N-φ模型与经典S-N曲线模型具有相似的数学表达式。与经典的S-N曲线模型相比，S-N-φ模型可以考虑初始静强度对疲劳寿命的影响，即能够考虑材料初始疲劳质量对疲劳寿命的影响。

利用初始静强度和疲劳寿命试验数据并结合式（12）可获得疲劳寿命累积分布函数

F N (n)

和参数

d

，然后可利用式（9）开展剩余强度预测。通过以上分析可知，本文方法不直接利用剩余强度试验数据求解剩余强度模型中的参数，在实际工程中非必要情况下可不开展剩余强度试验，进而节约试验成本。

3 算例

3.1 算例1

Feng等^［19］对［45/90/-45/0/45/0/-45/90/0］_S层合板进行了静强度和疲劳寿命的试验研究，初始静强度的均值为840.63 MPa，疲劳寿命试验数据如表1所示。

根据表1中的疲劳寿命试验数据，分别构建S-N-φ模型和经典S-N曲线模型，两个模型的预测结果见表2所示，图形结果如图1所示。表格中相对误差为

e r r = N P - N T N T × 100 %

（14）

式中：

N P

为预测值；

N T

为试验值。

表2 疲劳寿命预测结果（算例1）

应力/MPa	试验均值/次	本文模型		经典S-N模型
应力/MPa	试验均值/次	预测值/次	相对误差/%	预测值/次	相对误差/%
S ₁	1 404	1 331	-5.22	3 007	114.17
S ₂	18 083	20 023	10.73	12 442	-31.20
S ₃	102 985	113 174	9.89	56 125	-45.50
S ₄	482 271	366 711	-23.96	278 940	-42.16
S ₅	719 331	820 294	14.04	1 548 546	115.28

显示原图|下载原图ZIP|生成PPT

图1 疲劳寿命预测结果

表1　疲劳寿命试验数据（算例1）

从表2可以看出，文中模型和经典S-N曲线模型的最大相对误差分别为-23.96%和115.28%，相对误差绝对值的平均值分别为12.77%和69.66%，即文中模型对疲劳寿命的预测精度高于经典S-N曲线模型。

从图1可以看出，文中提出的疲劳寿命预测模型在对数坐标系中不是一条直线，主要是模型考虑了初始静强度对疲劳寿命的影响，在不同应力水平下参数

φ

的值是不一样的。

3.2 算例2

Gao等^［17］开展了［0/45/90/-45］₂ _S 层合板静强度和疲劳寿命的试验研究，初始静强度均值为760.36 MPa，疲劳寿命试验数据如表3所示。

表3 疲劳寿命试验数据（算例2）

应力/MPa	疲劳寿命/次
S ₁=669.12	530， 1 071， 2 214， 3 092， 5 031
S ₂=646.31	5 109， 6 350， 6 978， 10 288， 25 864
S ₃=623.50	11 966， 19 191， 27 895， 40 184， 51 185
S ₄=600.68	35 312， 51 444， 67 774， 87 143， 105 347
S ₅=577.87	100 530， 137 031， 188 306， 250 268， 374 645

3.2.1 疲劳寿命预测

根据表3中的疲劳寿命试验数据，分别构建S-N-φ模型和经典S-N曲线模型，两个模型的预测结果如表4所示，图形结果如图2所示。从表4可以看出，文中模型与经典S-N曲线模型的最大相对误差分别为15.92%和30.06%，相对误差绝对值的平均值分别为8.14%和17.23%。图2与数值计算结果表明，文中模型相比经典S-N曲线模型具有更高的预测精度。

表4 疲劳寿命预测结果（算例2）

应力/MPa	试验均值/次	本文模型		经典S-N模型
应力/MPa	试验均值/次	预测值/次	相对误差/%	预测值/次	相对误差/%
S ₁	2 388	2 521	5.58	3 106	30.06
S ₂	10 918	9 679	-11.35	8 617	-21.07
S ₃	30 084	30 005	-0.26	24 801	-17.56
S ₄	69 404	80 450	15.92	74 282	7.03
S ₅	210 156	194 206	-7.59	23 203	10.41

显示原图|下载原图ZIP|生成PPT

图2 疲劳寿命预测结果（算例2）

3.2.2 剩余强度预测

根据表3中的疲劳寿命试验数据，利用式（6）和（7）计算疲劳寿命在不同应力水平下的形状参数和尺度参数，如表5所示。基于表5中的形状参数和尺度参数，利用式（9）对不同应力水平下的剩余强度进行预测。在不同应力水平下，剩余强度的预测值与试验数据的对比如表6~8所示，表中试验均值来源于文献［17］。从表6~8可以看出，最大相对误差为-4.09%，说明改进剩余强度模型的预测精度是比较满意的。

表5 疲劳寿命的形状参数和尺度参数

应力/MPa	形状参数	尺度参数/次
S ₂=646.31	1.300 5	11 822.270 7
S ₃=623.50	2.012 1	33 949.729 2
S ₄=600.68	2.699 6	78 045.236 5

表6 剩余强度预测结果（ S=S ₂ ）

循环比	试验均值/MPa	预测值/MPa	相对误差/%
0.2	752.18	745.39	-0.90
0.4	742.65	721.58	-2.84
0.6	725.19	695.56	-4.09
0.8	688.92	670.01	-2.74

表7 剩余强度预测结果（ S=S ₃ ）

循环比	试验均值/MPa	预测值/MPa	相对误差/%
0.2	750.94	754.70	0.50
0.4	739.01	735.58	-0.46
0.6	718.63	704.35	-1.99
0.8	676.72	665.24	-1.70

表8 剩余强度预测结果（ S=S ₄ ）

循环比	试验均值/MPa	预测值/MPa	相对误差/%
0.2	749.58	758.20	1.15
0.4	735.72	744.86	1.24
0.6	712.66	713.32	0.09
0.8	664.54	622.98	-0.23

4 结论

（1）针对经典剩余强度模型需要剩余强度试验数据去拟合模型参数、模型构建成本较高的问题，本文从疲劳寿命累积分布函数角度出发，构建具有明确物理意义的损伤度，进而建立了改进剩余强度模型。改进剩余强度模型不需要剩余强度试验数据，仅需要初始静强度和疲劳寿命数据。

（2）基于改进剩余强度模型，构建了能够考虑初始静强度对疲劳寿命影响的S-N-φ疲劳寿命预测模型。与工程中广泛使用的经典S-N曲线模型相比，S-N-φ模型可以同时考虑初始静强度和应力水平对疲劳寿命的影响。

（3）算例结果表明，在疲劳寿命预测方面，S-N-φ模型相比经典S-N曲线模型具有更好的预测精度，其主要原因是S-N-φ模型考虑了初始静强度对疲劳寿命的影响；在剩余强度预测方面，改进剩余强度模型的预测精度是比较满意的，其主要原因是损伤度具有明确的物理意义，即强度衰减量与疲劳寿命累积分布函数一一对应。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	Schaff J R， Davidson B D. Life prediction metho-dology for composite structures，Part I：constant amplitude and two-stress level fatigue［J］. Journal of composite materials，1997，31（2）：128-157.

2	Wu F， Yao W.A fatigue damage model of compo- site materials［J］.International Journal of Fatigue， 2010， 32（1）：134-138.

3	Huston R J.Fatigue life prediction in composites［J］.International Journal of Pressure Vessels and Piping，1994，59（1）：131-140.

4	Wu F， Yao W.A model of the fatigue life distribution of composite laminates based on their static strength distribution［J］. Chinese Journal of Aeronautics， 2008， 21（3）：241-246.

5	俞耀，崔海涛，张宏建. 碳纤维树脂基单向板疲劳寿命预测模型［J］. 机械制造与自动化， 2021， 50（3）： 125-128.

6	徐蓉霞，高建雄，朱鹏年，等. 纤维增强复合材料层压板的疲劳寿命预测方法［J］. 上海交通大学学报， 2024，58（3）：400-410.

7	赵晟，张继文. 一种基于复合材料剩余强度的衍生疲劳损伤模型［J］. 复合材料学报， 2020， 37（10）： 2473-2481.

8	Montesano J， Selezneva M， Levesque M， et al. Modeling fatigue damage evolution in polymer matrix composite structures and validation using in-situ digital image correlation［J］. Composite Structures， 2015， 125：354-361.

9	Kang K， Lim D， Kim J. Probabilistic analysis for the fatigue life of carbon/epoxy laminates［J］. Composite Structures， 2008， 85（3）：258-264.

10	Kassapoglou C， Kaminski M.Modeling damage and load redistribution in composites under tension：tension fatigue loading［J］.Composites Part A：Applied Science and Manufacturing， 2011， 42（11）： 1783-1792.

11	拓宏亮，吴涛，卢智先，等. 复合材料层合板疲劳寿命预测方法研究［J］. 西北工业大学学报， 2022， 40（3）：651-660.

12	李嘉骞，沈海军. 复合材料层合板疲劳寿命形状参数与门槛值分析方法［J］. 国防科技大学学报， 2021， 43（3）：38-44.

13	Yao W X， Himmel N. A new cumulative fatigue damage model for bre-reinforced plastics［J］. Composites Science and Technology，2000，60（1）： 59-64.

14	Kassapoglou C. Fatigue life prediction of composi-te structures under constant amplitude loading［J］. Journal of composite materials，2007，41（22）： 2737-2754.

15	Mao H， Mahadevan S. Fatigue damage modeling of composite materials［J］. Composite Structures， 2002， 58（4）：405-410.

16	杨成鹏，冯炜森，林江嵘，等. 复合材料层压板疲劳性能评估的模型和方法［J］. 航空制造技术， 2023， 66（15）：40-59.

17	Gao J， Zhu P， Yuan Y， et al. Strength and stiffness degradation modeling and fatigue life prediction of composite materials based on a unified fatigue damage model［J］. Engineering Failure Analysis， 2022， 137（7）：106-290.

18	Gao J， An Z. A new probability model of residual strength of material based on interference theory［J］. International Journal of Fatigue， 2019，117（10）：202-208.

19	Feng Y， Ma B， Zhang T， et al. Reliability fatigue life and a new S-N curve model of composite laminates under tensile：tensile fatigue load［J］. Applied Composite Materials， 2021，28（1）：129-148.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 剩余强度模型

1.1 经典剩余强度模型

1.2 改进剩余强度模型

2 S-N-φ疲劳寿命预测模型

3 算例

3.1 算例1

表2 疲劳寿命预测结果（算例1）

图1 疲劳寿命预测结果

3.2 算例2

表3 疲劳寿命试验数据（算例2）

3.2.1 疲劳寿命预测

表4 疲劳寿命预测结果（算例2）

图2 疲劳寿命预测结果（算例2）

3.2.2 剩余强度预测

表5 疲劳寿命的形状参数和尺度参数

表6 剩余强度预测结果（ S=S 2 ）

表7 剩余强度预测结果（ S=S 3 ）

表8 剩余强度预测结果（ S=S 4 ）

4 结论

参考文献

表6 剩余强度预测结果（ S=S ₂ ）

表7 剩余强度预测结果（ S=S ₃ ）

表8 剩余强度预测结果（ S=S ₄ ）