1 问题描述与数学模型
2 聚类蚁群混合算法
2.1 聚类蚁群混合算法
2.2 初始种群的构造
2.3 信息素矩阵的产生与更新
表 1 不同等级解的判定及信息素携带量 |
| 等级 | 判定条件 | 信息素总量 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
2.4 新解生成方法
2.5 邻域算子设置
3 仿真实验
3.1 参数设置
表 2 参数设置实验案例数据 |
| 算例 | CN | CPC | 算例 | CN | CPC |
|---|---|---|---|---|---|
| A-n32-k5 | 32 | 6.4 | B-n45-k5 | 45 | 9 |
| A-n39-k5 | 39 | 7.8 | A-n63-k10 | 63 | 6.3 |
| A-n55-k9 | 55 | 6.11 | A-n80-k10 | 80 | 8 |
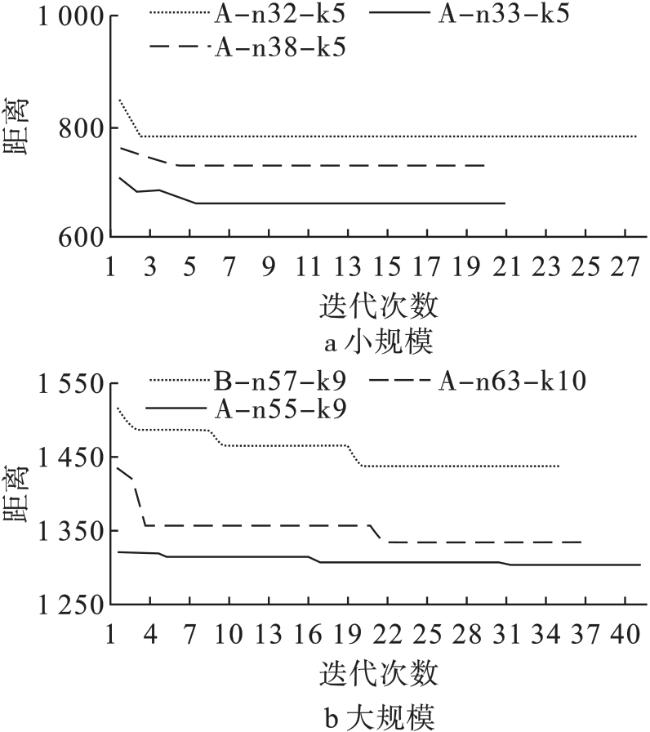
3.2 实验设置
表3 实验结果 |
| 算例 | BK | AVG | Aer | BEST | Ber | 算例 | BK | AVG | Aer | BEST | Ber |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A-n32-k5 | 784 | 785.53 | 0.20 | 784.00 | 0.00 | A-n69-k9 | 1 159 | 1 220.60 | 5.31 | 1 210.00 | 4.40 |
| A-n33-k5 | 661 | 664.87 | 0.58 | 661.00 | 0.00 | A-n80-k10 | 1 763 | 1 863.27 | 5.69 | 1 821.00 | 3.29 |
| A-n33-k6 | 742 | 742.00 | 0.00 | 742.00 | 0.00 | B-n31-k5 | 672 | 672.00 | 0.00 | 672.00 | 0.00 |
| A-n34-k5 | 778 | 778.73 | 0.09 | 778.00 | 0.00 | B-n34-k5 | 788 | 788.27 | 0.03 | 788.00 | 0.00 |
| A-n36-k5 | 799 | 811.27 | 1.54 | 805.00 | 0.75 | B-n35-k5 | 955 | 956.33 | 0.14 | 955.00 | 0.00 |
| A-n37-k5 | 669 | 675.53 | 0.98 | 670.00 | 0.15 | B-n38-k6 | 805 | 807.60 | 0.32 | 807.00 | 0.25 |
| A-n37-k6 | 949 | 967.33 | 1.93 | 960.00 | 1.16 | B-n39-k5 | 549 | 549.87 | 0.16 | 549.00 | 0.00 |
| A-n38-k5 | 730 | 732.47 | 0.34 | 730.00 | 0.00 | B-n41-k6 | 829 | 840.67 | 1.41 | 833.00 | 0.48 |
| A-n39-k5 | 822 | 826.20 | 0.51 | 825.00 | 0.36 | B-n43-k6 | 742 | 744.40 | 0.32 | 742.00 | 0.00 |
| A-n39-k6 | 831 | 834.13 | 0.38 | 833.00 | 0.24 | B-n44-k7 | 909 | 929.33 | 2.24 | 916.00 | 0.77 |
| A-n44-k6 | 937 | 956.27 | 2.06 | 943.00 | 0.64 | B-n45-k5 | 751 | 760.07 | 1.21 | 756.00 | 0.67 |
| A-n45-k6 | 944 | 981.47 | 3.97 | 968.00 | 2.54 | B-n45-k6 | 678 | 706.60 | 4.22 | 695.00 | 2.51 |
| A-n45-k7 | 1 146 | 1 159.93 | 1.22 | 1 149.00 | 0.26 | B-n50-k7 | 741 | 741.47 | 0.06 | 741.00 | 0.00 |
| A-n46-k7 | 914 | 924.73 | 1.17 | 917.00 | 0.33 | B-n50-k8 | 1 319 | 1 337.53 | 1.41 | 1 334.00 | 1.14 |
| A-n48-k7 | 1 073 | 1 100.80 | 2.59 | 1 093.00 | 1.86 | B-n51-k7 | 1 032 | 1 030.27 | -0.17 | 1 019.00 | -1.26 |
| A-n53-k7 | 1 010 | 1 034.07 | 2.38 | 1 020.00 | 0.99 | B-n52-k7 | 747 | 750.13 | 0.42 | 747.00 | 0.00 |
| A-n54-k7 | 1 167 | 1 194.00 | 2.31 | 1 186.00 | 1.63 | B-n56-k7 | 707 | 712.33 | 0.75 | 709.00 | 0.28 |
| A-n55-k9 | 1 073 | 1 115.00 | 3.91 | 1 087.00 | 2.42 | B-n57-k7 | 1 155 | 1 153.53 | -0.13 | 1 145.00 | -0.87 |
| A-n60-k9 | 1 354 | 1 377.53 | 1.74 | 1 369.00 | 1.11 | B-n57-k9 | 1 598 | 1 623.80 | 1.61 | 1 616.00 | 1.13 |
| A-n61-k9 | 1 034 | 1 082.93 | 4.73 | 1 070.00 | 3.48 | B-n63-k10 | 1496 | 1564.07 | 4.55 | 1 553.00 | 3.81 |
| A-n62-k8 | 1 288 | 1 338.27 | 3.90 | 1 323.00 | 2.72 | B-n64-k9 | 861 | 901.47 | 4.70 | 883.00 | 2.56 |
| A-n63-k10 | 1 314 | 1 362.07 | 3.66 | 1 335.00 | 1.60 | B-n66-k9 | 1 316 | 1 346.00 | 2.28 | 1 339.00 | 1.75 |
| A-n63-k9 | 1 616 | 1 686.73 | 4.38 | 1 664.00 | 2.97 | B-n67-k10 | 1 032 | 1 081.93 | 4.84 | 1 059.00 | 2.62 |
| A-n64-k9 | 1 401 | 1 459.13 | 4.15 | 1 437.00 | 2.57 | B-n68-k9 | 1 272 | 1 305.53 | 2.64 | 1 293.00 | 1.65 |
| A-n65-k9 | 1 174 | 1 256.07 | 6.99 | 1 209.00 | 2.98 | B-n78-k10 | 1 221 | 1 277.60 | 4.64 | 1 262.00 | 3.36 |