基于改进ReliefF-PNN的航空发动机起动系统异常状态识别

张雷鸣; 蒋丽英; 崔建国; 李贺; 刘明昆; 郭濠

doi:10.3969/j.issn.2095-1248.2023.06.010

沈阳航空航天大学学报 >

2023 , Vol. 40 >Issue 6: 68 - 75

DOI: https://doi.org/10.3969/j.issn.2095-1248.2023.06.010

信息科学与工程

基于改进ReliefF-PNN的航空发动机起动系统异常状态识别

张雷鸣 ,
蒋丽英 ,
崔建国 ,
李贺 ,
刘明昆 ,
郭濠

展开

沈阳航空航天大学自动化学院，沈阳 110136

张雷鸣(1998-),男,河南信阳人,硕士研究生,主要研究方向:飞行器故障诊断预测及综合健康管理,E-mail:1059483482@qq.com

蒋丽英(1976-),女,辽宁沈阳人,副教授,博士,主要研究方向:旋转机械系统故障特征提取,E-mail:jlylcb01@163.com。

收稿日期: 2023-11-08

网络出版日期: 2024-02-05

基金资助

国家自然科学基金(62003223)

收起

Abnormal state identification of aircraft engine starting system based on the improved ReliefF-PNN

Leiming ZHANG ,
Liying JIANG ,
Jianguo CUI ,
He Li ,
Mingkun LIU ,
Hao GUO

Expand

College of Automation，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2023-11-08

Online published: 2024-02-05

Fold

摘要

在航空发动机起动系统异常状态的识别研究中，起动系统的参数具有数据间相关性强、数据维度高、数据冗余信息多等特点。为降低数据维度，提高异常状态识别的准确率，将改进ReliefF算法与概率神经网络（probabilistic neural network，PNN）结合，提出改进ReliefF-PNN的航空发动机起动系统异常状态识别方法，更加有效地降低了参数的维度，并提升了异常状态识别模型的性能。利用该模型针对起动系统进行识别验证和分析。结果表明，利用改进后的ReliefF-PNN算法得到的参数子集进行异常状态识别的准确率优于改进前的结果，模型性能得到了进一步改善。

关键词： 发动机起动系统; 参数选择; ReliefF算法; 概率神经网络; 异常状态识别

本文引用格式

张雷鸣 , 蒋丽英 , 崔建国 , 李贺 , 刘明昆 , 郭濠 . 基于改进ReliefF-PNN的航空发动机起动系统异常状态识别[J]. 沈阳航空航天大学学报, 2023 , 40(6) : 68 -75 . DOI: 10.3969/j.issn.2095-1248.2023.06.010

Abstract

In the study of abnormal state identification of aircraft engine starting systems， the parameters of the starting system have characteristics such as strong correlation between data， high data dimensions and a lot of redundant information in data. In order to reduce the data dimension and improve the accuracy of abnormal state identification， an improved ReliefF algorithm was combined with probabilistic neural network（PNN） and improved ReliefF-PNN was proposed for abnormal state identification of aircraft engine starting system， which effectively reduced the dimension of parameters and improved the performance of the abnormal state identification model. The obtained model was used for identification verification and analysis of the starting system.The results show that the accuracy of using the improved ReliefF-PNN algorithm to identify abnormal states is better than before， further improving the performance of the model.

Key words： engine starting system; parameter selection; ReliefF algorithm; PNN; abnormal state identification

在航空工业领域，只有保证发动机的正常运行才能使飞行安全得到保障^［1］。发动机起动系统是发动机极其重要的子系统之一，其主要功能是将航空发动机从静止状态逐渐驱动至稳定的慢车状态。发动机要在各种不利环境因素作用下都能够在规定时间内完成起动过程。起动系统的异常状态识别能减少事故损失、保障生命财产安全^［2］，已成为评价发动机性能和航空服务质量的重要指标^［3］。

如今，人工智能技术被广泛应用到航空发动机的异常状态识别领域。梅晓川^［4］利用改进反向传播（back propagation，BP）神经网络建立发动机起动过程的动态模型，用于起动系统的模型辨识精度高、推广性好。林敏^［5］将核函数与极限学习机结合，提出一种基于核极限学习机的发动机故障诊断算法。通过气路部件复合数据及发动机真实试车数据验证，肯定了算法的有效性。Lomnicki等^［6］用数学方法建立了对象的异常状态识别与维修决策算法，数据驱动的方法论也随学者们的研究而逐渐完善。吕卫民等^［7］提出一种基于时间卷积神经网络和轻量级梯度提升机的航空发动机故障诊断方法，试验的仿真结果表明了所提方法的有效性，通过与其他模型的对比也体现了该方法的优越性。这些方法的不足之处在于没有重点探讨面对高维数据的参数选择问题，均针对将数据直接输入到算法模型中得到诊断率问题。

针对发动机起动系统参数数据具有维度高、冗余信息多、相关性强的特点，提出了一种基于改进ReliefF-PNN的航空发动机起动系统异常状态识别策略。从抽样方式、寻找K近邻样本的距离度量方式和筛选参数权重的阈值选择方式3方面对ReliefF算法进行了改进。使用改进ReliefF算法参数选择降低了起动系统原始数据维度，用筛选后的子集训练得到基于PNN的异常状态识别模型，验证后对比改进前得到了更高的准确率，效果良好。提出的改进ReliefF-PNN算法有效筛选出表征航空发动机起动系统异常状态的参数，降低了参数维度，提高了故障识别率。

1 改进ReliefF参数选择算法

参数选择是指根据某种评判标准，从原始参数的数据集中筛选出能够表征对象的子集数据，从而降低原始数据集的维度，能减少数据的计算量，节约模型资源；同时，提高算法的运行效率，令分类器高效工作；此外，可以使分类器的诊断精度得到有效提升，降低误判概率。

1.1 ReliefF算法

ReliefF算法是一种基于最近邻实例间距离计算和参数权重计算的经典参数选择算法，其广泛应用于多分类问题中^［8］。其基本思想是通过计算参数值对近邻实例分类的影响，来判断该参数对识别各模式的影响为正面或负面，进一步判断此参数的重要程度。在处理多分类问题时，每次从原始样本集中随机取出一个样本，然后按照评判规则来更新各项参数的权重，从而进行参数选择。

1.2 改进ReliefF算法

为解决传统ReliefF算法在应用于起动系统异常状态识别方面性能不足的问题，提出了一种改进的ReliefF参数选择方法，该方法从抽样方式、寻找K近邻样本的距离度量方式和筛选参数权重的阈值选择方式这3个方面对传统的算法进行了改进。

1.2.1 改进抽样方式

传统的ReliefF算法对原始数据集进行的单次抽样是从全体数据集中进行纯随机选择，这样可能会导致不同类的子集间抽样的次数相差较大，出现样本比例不均衡的问题，直接影响参数权重的分配，从而导致筛选出的参数子集不能有效表征系统异常状态。为避免这种情况发生，提出一种按比例约束的抽样方法。该方法在抽样流程中，保证各类别样本都能按照比例进行相对均衡地抽样。可以根据已有的样本数据，计算每个类别中的样本数量，并按照各类别样本数量的比例，把总的抽样次数分配给各个类别。

对于

n

种类别问题，假设总抽样次数为

M

，各类样本数为

N i (i = 1,2, ⋯, n)

，则抽样改进后第

i

类的随机抽样数量

M i

如式（1）所示

M i = N i ∑ i = 1 n N i × M

（1）

这样保证了样本的均衡性和全面性，在一定程度上保障了数据的合理性，可确保各类别的样本都能在一定程度上得到充分抽样，减少由于样本不均衡而影响参数权重分配的问题。

1.2.2 改进寻找K近邻样本的距离度量方式

在传统ReliefF算法中，通常采用欧氏距离或者曼哈顿距离等方法作为距离度量方式确定抽样样本的K个最近邻样本。然而，这两种常用的距离度量方法都存在各自的优劣：欧氏距离更具有连续性，但对离群点或异常值较为敏感；而曼哈顿距离受此影响较小且计算速度快，但直观性与连续性不及欧氏距离。欧氏距离存在的问题是对于参数较多的情况来说，样本间的距离受到少量参数变化的影响较大。曼哈顿距离则不同，它可以避免此问题，但不能较好地处理参数之间的相关性。

因此，针对寻找K近邻样本的距离度量方式，提出了一种加权距离度量方法，将欧氏距离和曼哈顿距离分别赋予权重并按照权重融合为一种新的加权距离度量方法。两个样本的加权距离表达式如式（2）所示

d n e w (x, y) = ω o × d o (x, y) + ω m × d m (x, y)

（2）

式中：

x

为随机抽样样本；

y

为其他样本；

d o (x, y)

和

d m (x, y)

分别为样本

x

与

y

的欧氏距离和曼哈顿距离；

ω o

和

ω m

为对应权重，且

ω o + ω m = 1

。其中，权重的计算表达式如式（3）、（4）所示

ω o = P m P o + P m

（3）

ω m = P o P o + P m

（4）

式中：

P o

和

P m

为抽样样本

x

到其他所有样本的欧氏距离均值和曼哈顿距离均值。

这种权重设置方式能综合考虑到两种常用距离度量方式对不同参数的适用情况，更全面地描述样本间的相似度或差异度。加权处理后能更有效地挖掘对权重贡献较大的参数^［9-10］。

1.2.3 改进筛选参数权重的阈值选择方式

传统ReliefF算法需要预先设置参数权重阈值，且通常是通过实验或经验来确定，而没有形成成熟的方法。因此，引入中值的概念，提出了自动设定参数权重阈值的方法。

将排序后的参数权重向量对应的中位数作为参数权重阈值。中值是一组按顺序排列数据的中间数，代表一个样本的值、总体或概率分布。将排序后的权重向量的中值作为阈值，借此对参数进行过滤来获取参数子集。对于按大小顺序排序后的参数权重向量

B = {b 1, b 2, ⋯, b N}

，

N

为参数个数，当

N

分别为奇数和偶数时，中值阈值

δ

的表达式如式（5）所示

δ = b N + 1 2 N 为奇 数 b N 2 + b 1 + N 2 2 N 为偶 数

（5）

对参数权重进行排序，并选择中值作为阈值进行过滤，筛选出相关性高的参数作为子集，剔除对分类有负面影响的冗余参数。

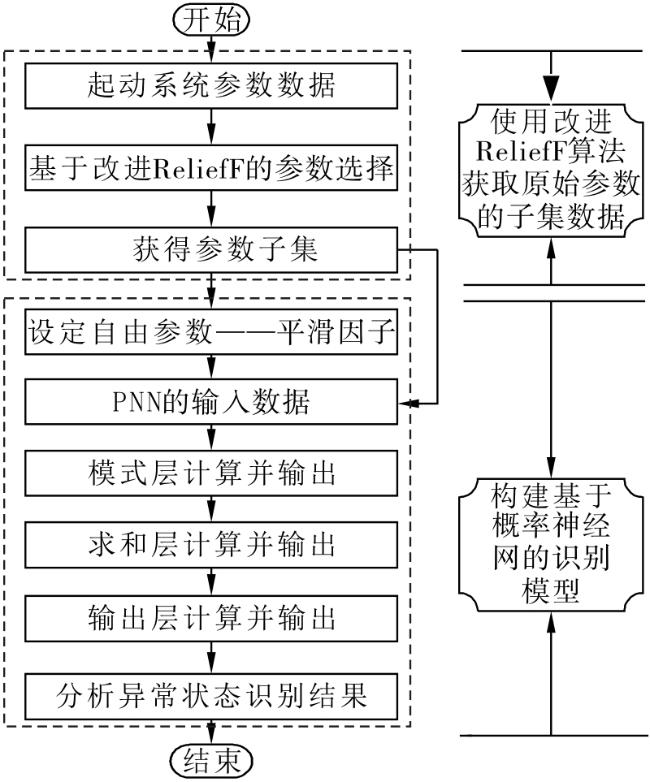
1.3 改进ReliefF算法的算法流程

改进ReliefF算法的算法流程如下：

步骤1：初始化参数的权重向量

A

，即令

A = {a 1, a 2, ⋯, a N}

，其中

a i (i = 1,2, ⋯, n)

为第

i

个参数的权值。

步骤2：确定各类随机抽样样本数。假设原始数据集

D

共包含

n

种类别，每种样本数为

N i (i = 1,2, ⋯, n)

。按照式（1）计算出每种类别随机抽样样本总数

M i

。

步骤3：确定每个子集中样本的k近邻。从原始数据集

D

中的

n

类样本随机选择样本

R i (i = 1,2, ⋯, M)

。先按照式（2）中新的距离度量方式，找出样本

R i

在同类样本中的

k

个近邻样本

H j (j = 1,2, ⋯, k)

。再从不同于

R i

的其他类别的样本中，分别找出

k

个近邻样本

N R j (j = 1,2, ⋯, k)

。

步骤4：更新参数权重。计算各参数对应的参数权重

a i (i = 1,2, ⋯, n)

。更新权重的表达式如式（6）所示

a i = a i - ∑ j = 1 k d i f f (a i, R i, H j) M · k + ∑ j = 1 k p (C) 1 - p c l a s s (R i) ∑ j = 1 k d i f f (a i, R i, N R j M · k

（6）

式中：

c l a s s (R i)

表示样本

R i

所属类别；

C

表示不同于样本

R i

所属类的其他类别；

p (*)

表示括号内类别在全样本中占的数量百分比。

同类样本和不同类样本的计算公式为

d i f f a i, R i, H j = R i [a i] - H j [a i] m a x (a i) - m i n (a i)

（7）

d i f f a i, R i, N R j = R i [a i] - N R j [a i] m a x (a i) - m i n (a i)

（8）

式中：

R i [a i]

、

H j [a i]

和

N R j [a i]

表示该样本在第

i

个参数的数值。

步骤5：遍历各项参数，分别计算各参数权重。权重越大表明此参数对分类越重要；反之，表示该参数的重要性较低^［11］。返回步骤3直到按照式（2）中各抽取样本的计算过程全部结束。

步骤6：把经过计算之后的参数权重向量

A = {a 1, a 2, ⋯, a N}

按大小排序，形成参数权重向量

B = {b 1, b 2, ⋯, b N}

。通过式（3）~（5）计算中的值得到权重阈值

δ

，对参数进行过滤筛选。

步骤7：输出参数子集

Z

，其中

Z ⊆ D

。

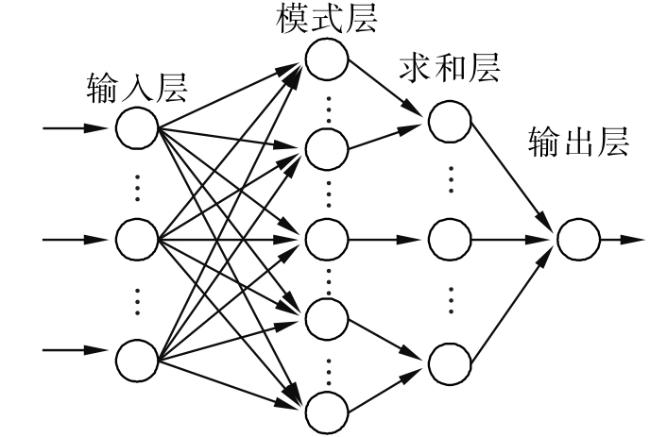
2 基于PNN的异常状态识别模型

人工神经网络具有较好的处理非线性数据能力，它被广泛用于异常状态识别中。1989年由Specht^［12］首次提出概率神经网络，它是基于贝叶斯最小风险决策规则分类的前向传播神经网络，易使用且泛化精度高^［13］。其学习速度快、结构简单的优点有利于起动系统模式识别系统的搭建^［14］，采用此方法可进行起动系统的异常状态识别。其结构如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 PNN结构示意图

概率神经网络各层结构如下：

（1）输入层

从训练数据集中接收样本向量，将其发送给PNN。神经元个数与样本向量的长度相等，输入层的神经元个数等于样本数据的维数。

（2）模式层

模式层的每个神经元对应一个中心，功能是将输入层得到的样本向量与训练数据进行比较，并计算与类别的相关度。唯一自由参数为平滑因子

ε

，决定模型性能并影响识别准确率。

（3）求和层

求和层功能是将样本判定为某类发生的概率进行累加，把归于同类的概率相加求和，得出各类的概率估计密度函数。神经元的输出和判断与某类发生的概率密度估计值成正比，进行标准化处理后输入到输出层。此层的神经元数量与样本的类别数相同。

（4）输出层

输出层的功能是把求和层中计算的概率密度估计进行比较，并输出最大估计值对应的类别。神经元个数等同样本类别数，概率密度函数最大的类别对应的输出为1，表示样本被判定为此类别，其余神经元输出皆为0。

3 基于改进ReliefF-PNN的起动系统异常状态识别

在起动系统异常状态识别的应用里，关键问题之一是在数据采集分析的过程中进行有效的参数选择^［15］。选择最能表征对象的参数是异常状态识别的重要一步^［16］，能提高模型的泛化能力，减少数据挖掘的信息冗余。

为提高发动机起动系统异常状态识别的精度，结合采集的某型发动机起动系统的原始数据，提出一种基于改进的ReliefF-PNN 的起动系统状态识别方法。

离线建立模型流程如图2所示，步骤如下：

显示原图|下载原图ZIP|生成PPT

图2 基于改进ReliefF-PNN的异常状态识别流程图

步骤1：参数选择。用改进ReliefF算法对发动机起动系统进行参数选择，过滤筛选之后的参数数据组成最有代表性的参数子集。

步骤2：建立PNN概率神经网络模型。设定概率神经网络中的自由参数^［17］——平滑因子

ε

，一般

ε ∈ (0,1)

。将从步骤1得到的参数子集的样本向量作为概率神经网络的输入，即作为训练数据建立PNN异常状态识别模型。

异常状态识别过程如下：

步骤1：参数采集。针对原始的全部参数数据，按照选择的最优参数来采集获取参数数据信息，从而得到参数子集的数据。

步骤2：利用PNN模型来计算异常状态识别结果。将参数样本向量送入输入层，分别计算模式层、求和层以及输出层的结果。通过最后输出的识别结果来进一步分析模式识别准确率。

4 起动系统异常状态识别分析

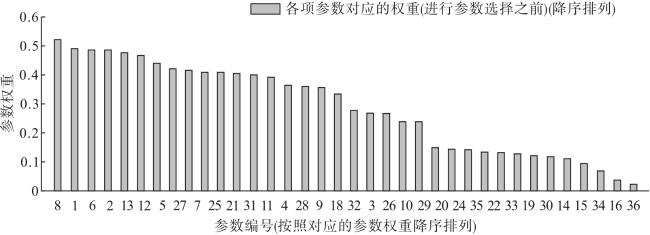
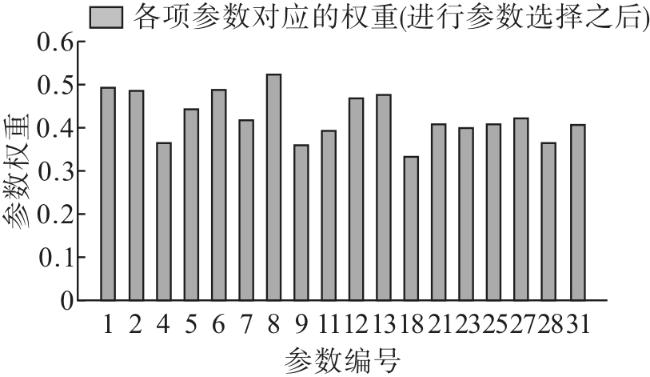
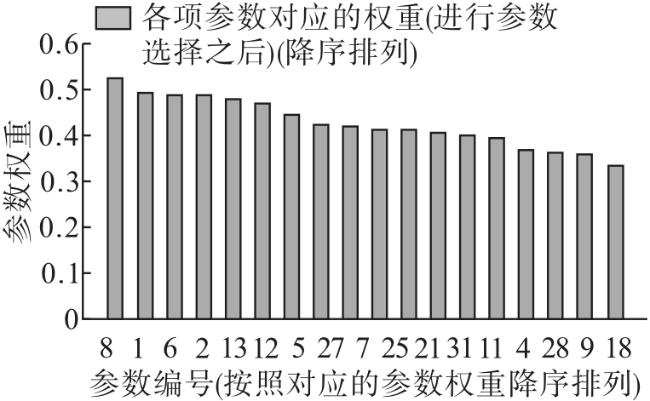
本文的实验对象是某型航空发动机起动系统，该系统包含空气总温、滑油液位、气压高度等36维参数，以及健康、起动超温故障、转速悬挂故障、压气机喘振故障、切油故障5种状态模式。

4.1 基于改进ReliefF起动系统参数选择

作为研究对象的发动机起动系统一共有36维参数，它们可以被分为5种类别，用改进ReliefF算法得到各项参数的权重，参数选择前各项参数的原始权重及按降序排序后的权重如图3~4所示。

显示原图|下载原图ZIP|生成PPT

图3 原始参数权重

显示原图|下载原图ZIP|生成PPT

图4 原始参数权重（降序排列）

作为被研究对象的发动机起动系统的参数为36维，以中值作为参数权重的阈值，进行参数选择之后的参数为18维。参数选择后的参数及降序排列后的结果如图5~6所示。

显示原图|下载原图ZIP|生成PPT

图5 参数选择结果

显示原图|下载原图ZIP|生成PPT

图6 参数选择结果（降序排列）

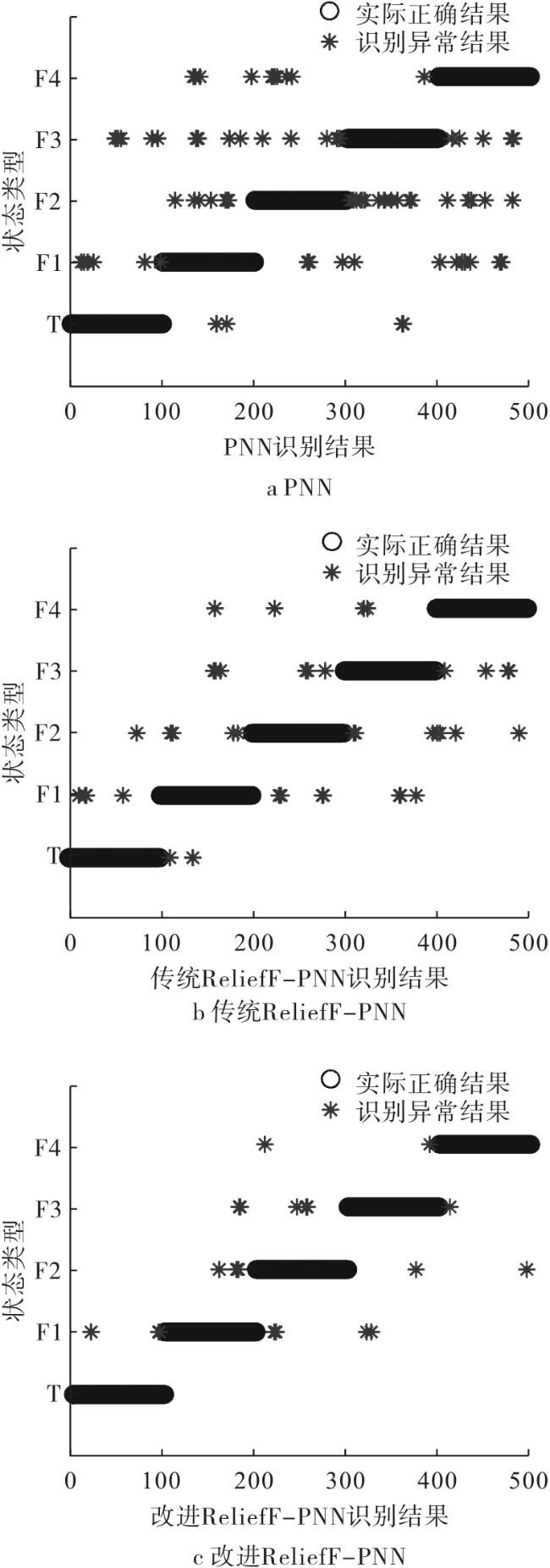
4.2 起动系统异常状态识别

采用基于改进ReliefF-PNN的异常状态识别方法对飞机发动机起动系统进行实验验证，根据某型飞机发动机起动系统不同状态数据集来设置标签。针对飞机发动机起动系统的5种不同典型状态，按照4：1的比例选取2 000组样本构建训练样本集和500组样本作为测试集。训练样本中各类均为400组，测试样本中各类均为100组。数据的各项信息如表1所示。

表1 起动系统5种状态对应的数据信息

状态	标签	训练样本数	测试样本数
健康	T	400	100
起动超温故障	F1	400	100
转速悬挂故障	F2	400	100
压气机喘振故障	F3	400	100
切油故障	F4	400	100

分别用传统ReliefF算法获得的参数和改进ReliefF算法获取的数据进行训练，利用测试集对其进行实验验证，同时结合对照不使用参数选择算法的PNN作为对比，3种模型的异常状态识别结果如图7所示。

显示原图|下载原图ZIP|生成PPT

图7 异常状态识别结果

采用表1测试集中的测试样本对其进行实验验证。500组测试数据在3种模型中各有423组、461组和479组的诊断结果与实际相符，有77组、39组和21组的结果与实际不符。3种模型的异常状态识别准确率如表2所示。

表2 3种识别模型的准确率对比

识别模型	测试样本	识别正确样本	准确率
PNN	500	423	84.6%
传统ReliefF-PNN	500	461	92.2%
改进ReliefF-PNN	500	479	95.8%

由图7和表2可知，改进ReliefF-PNN发动机起动系统异常状态识别模型相较于传统PNN模型和传统ReliefF-PNN模型，进一步提高了识别的准确率，绝大部分数据都被正确分类，准确率为95.8%。而前两者的识别模型的准确率只有84.6%和92.2%。

5 结论

（1）本文提出改进ReliefF-PNN算法对5种状态类别的航空发动机起动系统数据进行了参数选择。选择出了能有效表征起动系统状态的18维最优特征参数，有效实现了参数降维，且进一步提高了异常状态识别的准确率。

（2）通过对比PNN模型和传统ReliefF-PNN模型，可以发现在数据样本相同的情形下，利用改进ReliefF-PNN算法模型有着更高的识别准确率。

（3）在以后的相关应用中，可考虑选择基于改进ReliefF-PNN的发动机起动系统异常状态识别方法，此方法经过实验验证效果较好。该方法进一步解决了由于起动系统参数种类繁杂而导致传统参数选择算法仍会出现识别准确率不理想的问题，有效提升了发动机起动系统的异常状态识别效能，具有一定的应用价值，有着较好的推广应用前景。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	李东辉，喻甲其，杨梅.航空发动机故障诊断与研究［J］.设备管理与维修，2022，42（5）：148-149.

2	Liu X B， Tu J C， Shen L N.The application of the improved genetic algorithm in the aeroengine fault diagnosis［J］.Advanced Materials Research，2013（846/847）：840-843.

3	陈冰.面向智能制造的航空发动机协同设计与制造［J］.航空制造技术，2016，59（5）：16-21.

4	梅晓川.基于改进BP网络的航空发动机起动过程辨识［J］.航空计算技术，2009，39（6）：58-61.

5	林敏.极限学习机在航空发动机气路故障诊断中的应用［D］.上海：上海交通大学，2016.

6	Lomnicki Z A， Barlow R E， Proschan F，et al.Mathematical theory of reliability［J］.Mathematical Reviews，1966，17（2）：213.

7	吕卫民，孙晨峰，任立坤，等.一种基于TCN-LGBM的航空发动机气路故障诊断方法［J/OL］.兵工学报，1-11（2023-01-30）［2023-10-29］.

8	Urbanowicz R J， Meeker M， La Cava W，et al.Relief-based feature selection：introduction and review［J］.Journal of Biomedical Informatics，2018（85）：189-203.

9	董智博.基于改进欧氏距离的三维点云分割算法分析研究［D］.北京：华北电力大学，2022.

10	王桥梅，吴浩，杨杰，等.基于曼哈顿距离的HVDC输电线路故障识别新方法［J］.四川轻化工大学学报（自然科学版），2022，35（4）：75-84.

11	孙林，杜雯娟，李硕，等.基于标记相关性和ReliefF的多标记特征选择［J］.西北大学学报（自然科学版），2022，52（5）：834-846.

12	Specht D F.Probabilistic neural networks［J］.Neural Networks，1990，3（1）：109-118.

13	陈佳豪，吴浩，胡潇涛，等.基于LMD和DE-PNN的高压断路器机械故障识别方法［J］.计算机应用与软件，2023，40（6）：57-62，165.

14	陈立爱，俞宏艳，汪佳奇，等.基于PCA-SSA-PNN的齿轮故障诊断［J］.长沙大学学报，2023，37（2）：18-27.

15	Sun L， Zhang J X， Ding W P，et al.Feature reduction for imbalanced data classification using similarity-based feature clustering with adaptive weighted K-nearest neighbors［J］.Information Sciences，2022（593）：591-613．

16	赵舒安.基于数据驱动模型的航空发动机剩余使用寿命预测及故障诊断研究［D］.重庆：重庆邮电大学，2022．

17	祝钊，曹鹏.基于改进PSO-PNN的大螺旋钻机故障诊断系统研究［J］.煤炭工程，2022，54（11）：193-198．

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 改进ReliefF参数选择算法

1.1 ReliefF算法

1.2 改进ReliefF算法

1.2.1 改进抽样方式

1.2.2 改进寻找K近邻样本的距离度量方式

1.2.3 改进筛选参数权重的阈值选择方式

1.3 改进ReliefF算法的算法流程

2 基于PNN的异常状态识别模型

图1 PNN结构示意图

3 基于改进ReliefF-PNN的起动系统异常状态识别

图2 基于改进ReliefF-PNN的异常状态识别流程图

4 起动系统异常状态识别分析

4.1 基于改进ReliefF起动系统参数选择

图3 原始参数权重

图4 原始参数权重（降序排列）

图5 参数选择结果

图6 参数选择结果（降序排列）

4.2 起动系统异常状态识别

表1 起动系统5种状态对应的数据信息

图7 异常状态识别结果

表2 3种识别模型的准确率对比

5 结论

参考文献