1 BP神经网络和分数阶BP神经网络的理论介绍
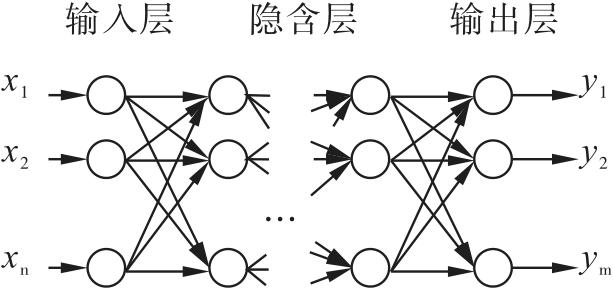
1.1 神经网络结构
1.2 BP神经网络的学习算法
1.2.1 信息正向传播的过程
1.2.2 误差反向传播过程
1.3 BP神经网络的优势与局限性
1.3.1 BP神经网络的优势
1.3.2 BP神经网络的局限性
1.4 分数阶微积分的定义
1.5 基于分数阶Caputo定义的BP算法
2 滚动轴承故障诊断分数阶BP神经网络模型的建立与训练
2.1 时域特征参数的选取
2.2 建立分数阶BP神经网络
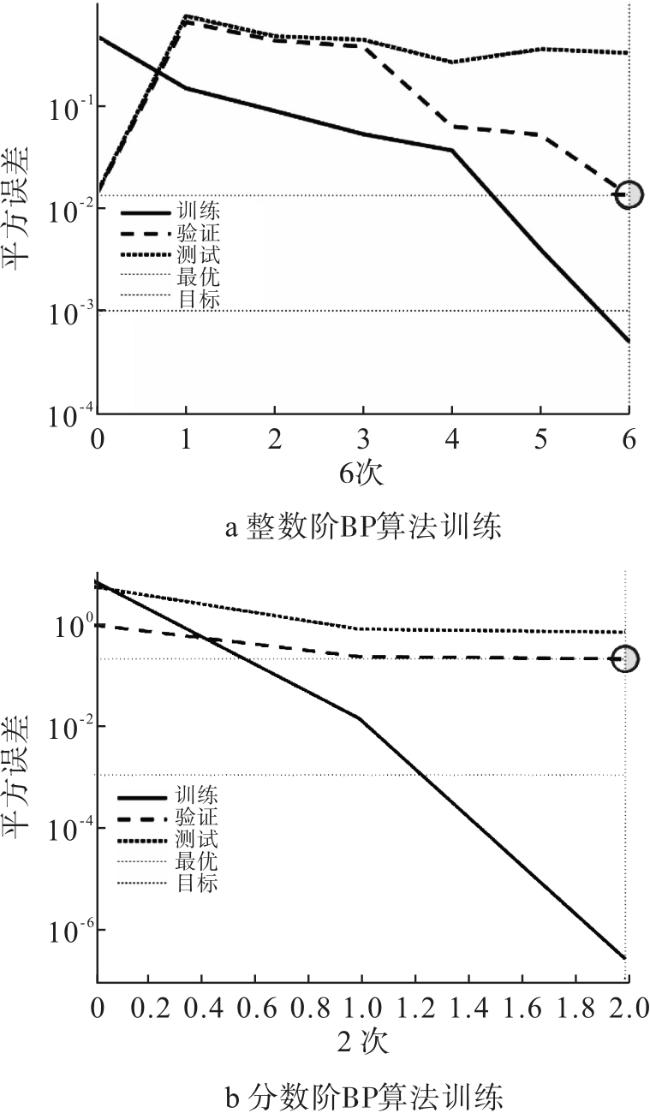
2.3 训练分数阶BP神经网络
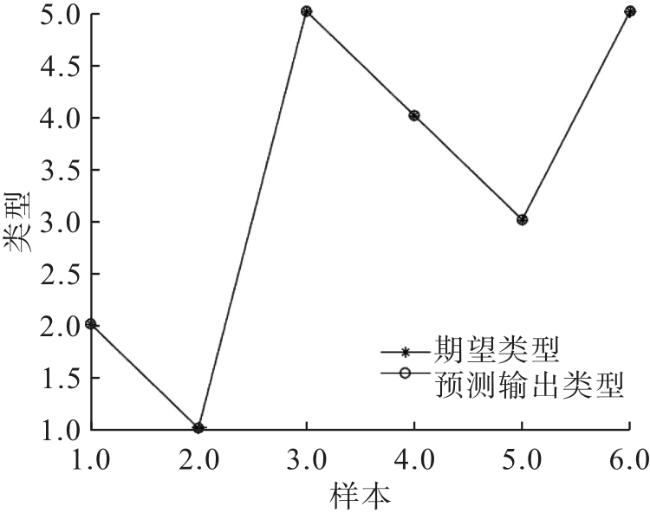
3 实验验证
表1 测试样本数据及故障类型 |
| 样本序号 | 测试样本数据 | 故障类型 |
|---|---|---|
| 1 | 0.549 3 0.262 6 0.265 9 0.308 8 0.222 1 | 内圈故障 |
| 2 | 0.003 1 0.023 5 0.000 5 0.0030 0.004 5 | 正常 |
| 3 | 0.992 0 0.989 9 0.997 9 0.993 7 0.797 9 | 保持架故障 |
| 4 | 0.670 4 0.497 2 0.523 5 0.474 1 0.979 1 | 滚动体故障 |
| 5 | 0.257 2 0.100 6 0.095 8 0.098 1 0.089 0 | 外圈故障 |
| 6 | 0.980 0 0.982 5 0.983 5 0.988 7 0.800 0 | 保持架故障 |