高空台空气起动系统的无模型自适应迭代学习控制

岑游彬; 齐义文; 李鑫; 彭晋; 李贺

doi:10.3969/j.issn.2095-1248.2023.05.010

沈阳航空航天大学学报 >

2023 , Vol. 40 >Issue 5: 75 - 81

DOI: https://doi.org/10.3969/j.issn.2095-1248.2023.05.010

信息科学与工程

高空台空气起动系统的无模型自适应迭代学习控制

岑游彬 ^,¹ ,
齐义文 ^,¹ ,
李鑫 ² ,
彭晋 ² ,
李贺 ¹

展开

^1. 沈阳航空航天大学自动化学院，沈阳 110136
^2. 中国航发四川燃气涡轮研究院整机试验研究室，绵阳 621703

岑游彬(1998-),男,浙江宁波人,硕士研究生,主要研究方向:高空台智能控制,E-mail:110243347@qq.com

齐义文(1983-),男,辽宁丹东人,教授,博士,主要研究方向:先进动力系统与智能控制,E-mail:qiyiwen@gmail.com。

收稿日期: 2023-09-28

网络出版日期: 2023-12-22

基金资助

国家自然科学基金(62003223)

航空发动机及燃轮机基础科学中心项目(P2022-B-V-001-001)

收起

Model􀆼free adaptive iterative learning control for high􀆼altitude air􀆼starting system

Youbin CEN ^,¹ ,
Yiwen QI ^,¹ ,
Xin LI ² ,
Jin PENG ² ,
He LI ¹

Expand

^1. College of Automation，Shenyang Aerospace University，Shenyang 110136，China
^2. Whole Machine Test Laboratory AECC Sichuan Gas Turbine Establishment，Mianyang 621703，China

Received date: 2023-09-28

Online published: 2023-12-22

Fold

摘要

针对高空台空气起动系统存在非线性、强耦合性、大延迟、不确定性等问题，提出了一种基于Smith估计的高空台空气起动系统无模型自适应迭代学习控制算法。首先，利用Smith估计器，估计和补偿系统延迟误差；其次，基于系统输入和输出数据，获得高空台空气起动系统的动态线性化数据模型；最后，提出高空台空气起动系统的无模型自适应迭代学习控制方法，通过不断更新每轮的控制器，实现系统的快速精准调节。仿真结果表明，随着迭代次数的增加，所提出方法能减小系统跟踪误差，修正系统输出跟踪轨迹。同时，相较于单纯的无模型自适应迭代学习控制算法，加入Smith估计器补偿延迟后，系统动态性能可得到显著改善，验证了所提算法的可行性和有效性。

关键词： 高空台空气起动系统; 无模型自适应控制; 迭代学习控制; Smith估计器; 延迟系统

本文引用格式

岑游彬 , 齐义文 , 李鑫 , 彭晋 , 李贺 . 高空台空气起动系统的无模型自适应迭代学习控制[J]. 沈阳航空航天大学学报, 2023 , 40(5) : 75 -81 . DOI: 10.3969/j.issn.2095-1248.2023.05.010

Abstract

Aiming at the problems of nonlinearity，strong coupling，large delay and uncertainty of the air-starting system at high-altitude，a model-free adaptive iterative learning control algorithm for air -starting system based on Smith estimation was proposed. Firstly，the Smith estimator was used to estimate and compensate for the system delay error. Secondly，based on the input and output data of the system，the dynamic linearized data model of the high-altitude platform air starting system was obtained. Finally，a model-free adaptive iterative learning control method for the high-altitude platform air starting system was proposed，which continuously updated the control law for each round to achieve rapid and accurate adjustment of the system. Simulation results show that with the increasing of iteration times，the proposed method can reduce the system tracking error and correct the system output tracking trajectory. Meanwhile，compared to the simple model-free adaptive iterative learning control algorithm，the dynamic performance of the system is improved significantly after joining Smith estimator，which verifies the feasibility and effectiveness of the proposed algorithm.

Key words： high-altitude platform air starting system; model-free adaptive control; iterative learning control; Smith estimator; delay system

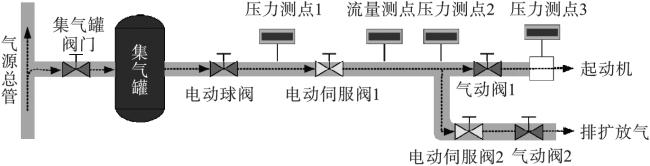
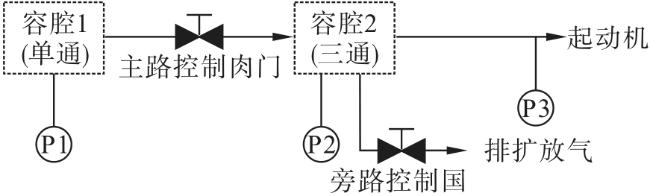
高空试车台（简称高空台）是对发动机整机和部件进行试验的关键设备，能模拟高空飞行条件和环境，对研制和改进航空发动机具有重要作用。对于高空台，空气起动系统是验证航空发动机起动性能并探索空中起动特性的关键设备，其控制性能直接决定了高空台相关验证试验的成败。该系统主要由高压气源、各类型阀门以及管道等构成^［1］。相较于电起动或燃气涡轮起动，空气起动系统通过调节空气涡轮入口压力来实现起动机的旋转，进而利用传动装置将航空发动机带至起动状态^［2］。该系统输出扭矩大、结构简单、工作稳定可靠。然而，在试验过程中，系统的工作部件多、阀门和管道结构耦合关联、环境和工况复杂^［3］，这些因素都对空气起动系统，尤其对其空气涡轮入口压力的调节产生较大干扰。因此，亟需研究和开发新型高空台空气起动系统的智能控制方法，以消除各种干扰因素的影响，并使其能够适应不同工况下的起动过程要求。

当前，在高空台空气起动系统控制领域，PID控制依旧是主流方法。例如，雷勇等^［4］针对台架试验中空气起动系统存在的定常阶跃扰动，设计了一种动态前馈补偿和PID反馈组成的复合控制器，有效提高了空气起动系统的抗扰动特性。另外，高空台进气压力模拟系统与空气起动系统结构相似，相关控制方案的研究较多。朱美印等^［5］针对高空台进气系统在全工作范围的精确控制问题，提出一种PI增益调度控制方法。赵涌等^［6］提出一种复合控制技术，将PID与模糊控制相结合，构成兼具两者优点的压力模拟控制系统。钱秋朦等^［7］基于自抗扰控制器，提出一种具有主动抗扰机制的进气压力控制方法，大幅提升了发动机过渡态试验中进气系统的调节品质。

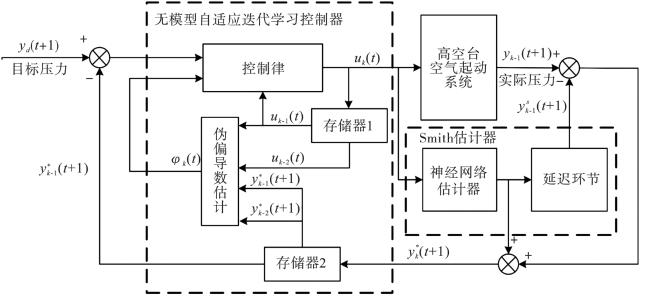
高空台空气起动系统涉及部件多，系统参数复杂，基于模型的控制有时难以获得更好的控制效果。无模型自适应控制是一种无需建立过程模型的自适应控制方法^［8］，它利用系统输入输出信息建立等效线性化模型，并引入伪偏导数估计器实现参数自适应调节。在此基础上，无模型自适应迭代学习控制^［9］无需高精度模型，每次迭代的控制输入都会在以往控制量的基础上根据跟踪误差来修正，以获得更好的性能。作为主要执行机构，阀门对系统输出起决定性作用。然而，阀门为典型大延迟环节，易产生超调振荡，如何避免延迟是控制系统必须解决的问题。本文采用Smith估计器来补偿阀门响应延迟对控制系统的影响^［10］。

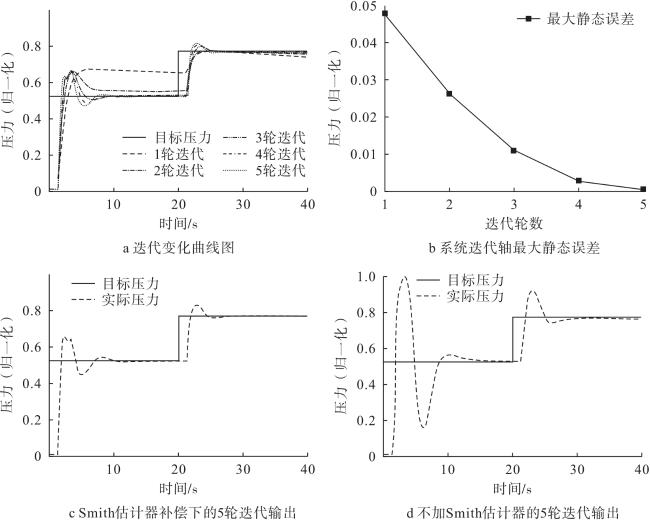
综上，本文针对现有高空台空气起动系统建模复杂、模型耦合性强、基于模型的控制方法适用性不足等缺点，提出一种基于Smith估计的高空台空气起动系统无模型自适应迭代学习控制方法。首先，利用输入输出数据，建立系统动态线性化模型；然后，根据系统模型设计无模型自适应迭代学习控制器。仅利用系统跟踪误差与控制信号输入，并通过迭代更新的方式不断修正控制量，达到完全跟踪期望信号的目的，而在控制器设计过程中无需系统模型参数。同时，利用Smith估计器可以有效补偿延迟时间对系统稳定性的影响。

1 空气起动系统建模

1.1 空气起动系统工作原理

如图1所示，空气起动系统各阀门包括集气罐阀门、电动球阀、电动伺服阀1、气动阀1、电动伺服阀2和气动阀2。其中电动伺服阀1为主路控制阀门，电动伺服阀2为旁路控制阀门，图中箭头方向为气流流通方向。系统工作原理如下：首先，电动球阀全关，集气罐阀门全开，待充满后，关闭集气罐阀门。然后，使电动球阀、气动阀1和气动阀2根据试验所需保持恒定开度。最后，通过改变主路和旁路阀门的开度调节压力测点3，以满足空气涡轮入口目标压力的指标。

显示原图|下载原图ZIP|生成PPT

图1 空气起动系统组成结构图

1.2 主路/旁路控制阀建模

试验过程中，空气起动系统主路控制阀门和旁路控制阀门的动态特性直接决定系统性能。由于其余阀门在试验过程中保持特定开度，故可通过使用折合流量计算压力动态特性的方法。控制阀门是典型的节流元件，也是高空台空气起动系统的最终执行元件，主路/旁路控制阀门的工作原理与孔板类似，在控制阀门动态特性建模时将其等效为孔板。对于空气等可压缩介质，在绝热等熵条件下可推导出控制阀门的流量公式^［11］如式（1）所示

Q m = u 2 1 - u 2 m 2 p r 2 k k p r 2 k k - 1 1 - p r k - 1 k 12 A 0 2 ρ p 1

（1）

式中：p₁ 为阀前压力；p_r 为阀后与阀前压力之比；ρ为阀前气体密度；k为气体绝热指数；A₀ 为调节阀等效截面积；u为流束收缩系数，它等于流束收缩最小截面积与节流孔面积之比；m为调节阀等效截面积与管道截面积之比；Q_m 为质量流量。

令式（1）中的第一个根号项为φ，称其为流量系数，则得到简化后的流量公式^［12］

Q m = φ A 0 2 ρ p 1

（2）

由式（1）可知，流量特性φ与压比和调节阀等效截面积有关，而调节阀等效截面积可以通过开度与最大截面积乘积进行换算。因此，通过试验数据和修正算法^［13-14］最终得到流量系数特性表，如表1所示，该特性表用于描述流量特性随着开度和压比变化的关系。

表1 阀门流量系数特性表

α	p_r
α	0	0.1	0.2	···	1
0	0.350 00	0.226 00	0.138 00	···	0.002 83
0.1	0.342 00	0.219 00	0.136 00	···	0.002 80
0.2	0.327 00	0.215 00	0.132 00	···	0.002 70
···	···	···	···	···	···
0.9	0.061 00	0.052 00	0.046 00	···	0.000 66
1	0.000 00	0.000 00	0.000 00	···	0.000 00

1.3 管道容腔建模

对于空气起动系统而言，其排气管路较为复杂，不同流路的气流会在双通、三通等结构内掺混，在管道出口流出。从结构角度分析，排气管路分别与集气罐、各类型阀门和空气起动机连接，各部件特性耦合关联复杂，排气管道动态特性直接影响整个空气起动系统性能。同时，集气罐在工作时，气体外排导致罐体压力下降，该特性也会对空气起动系统造成较大影响。因此，将集气罐和排气管道等效为容腔模型，分析其动态特性机理，建立部件级空气起动系统容腔模型，可对真实起动过程进行模拟。深入分析集气罐和各排气管道气体流通特性，为实际试验过程和平台改进改型提供可靠的借鉴和仿真验证。

图2为空气起动系统简化图，由于电动球阀和气动阀1开度恒定，因此可以将集气罐至主路控制阀门前的部分简化等效为容腔1，将主路控制阀门后至起动机和旁路阀门前的部分简化等效为容腔2。对于此空气起动系统而言，简化得到的容腔2虽然为三通（单进双出）结构，但双出的管道容腔压力和温度近似相等，将三通结构的容腔出口流量相加，可进一步简化为双通结构。

显示原图|下载原图ZIP|生成PPT

图2 空气起动系统简化图

图3为化简后的容腔双通结构，在不考虑管道壁面换热的情况下，通过管道内壁气体状态方程、管路流量连续性方程、内部储能方程和热力学变化方程^［15］得到容腔内压力和温度的微分方程为

d p d t = R V d (c p - R) (c p 1 Q m 1 T 1 - c p Q m T)

（3）

d T d t = R T p V d (c p - R) (c p 1 Q m 1 T 1 - c p Q m T) - R T 2 p V d (Q m 1 - Q m)

（4）

式中：p和T分别表示管道内壁内气体压力和温度；

T 1

表示进气温度；

V d

表示容腔等效容积；

Q m 1

和

Q m

分别表示容腔进气、排气流量；

c p 1

和

c p

分别表示进气、排气比定压热容；

R

表示气体常数。

显示原图|下载原图ZIP|生成PPT

图3 双通容腔图

2 Smith估计器设计

如图4所示，系统运行时，在气源控制阀门和电动球阀全开的同时，无模型自适应迭代学习控制器开始对主路控制阀门进行调节，旁路控制阀保持50%开度恒定。为解决系统延迟导致控制器超调振荡的问题，加入Smith估计器^［16］，补偿延迟特性所带来的误差，如式（5）所示

y k * t + 1 = y k s t + 1 - τ + y k t + 1 - y k s t + 1

（5）

式中：

y k s t + 1

表示Smith估计器的输出；

τ

表示系统延迟时间；

y k s t + 1 - τ

表示神经网络对高空台空气起动系统无延迟输出预估^［17］；

y k t + 1

表示空气起动系统实际输出；

y k * t + 1

表示Smith估计器补偿后的系统输出。

显示原图|下载原图ZIP|生成PPT

图4 基于Smith估计的空气起动系统无模型自适应迭代学习控制框图

假设Smith估计器能完全估计系统参数，则根据式（5）有

y k * t + 1 = y k s t + 1 - τ ≈ y k t + 1 - τ

（6）

3 无模型自适应迭代学习控制器设计

3.1 高空台空气起动系统动态线性化

通过Smith估计器可得到高空台空气起动系统补偿输出

y k * t + 1

，进而，可利用该输出量设计无模型自适应迭代学习控制器。高空台空气起动系统可通过如式（7）所示的单输入单输出的非线性离散时间方程描述

y k * (t + 1) = f y k * (t), y k * (t - 1), ⋯, y k * (t - n y), u k (t), u k (t - 1), ⋯, u k (t - n u)

（7）

式中：

u (t) 和 y * (t)

分别为主路控制阀开度和Smith估计器补偿压力；

f (⋅)

表示未知的非线性函数；n_y 和n_u 分别表示系统的未知阶数；

t ∈ 0,1, …, N

表示采样时刻；

k ∈ 0, 1, …

表示迭代轮次。接着，给出以下3个假设：

假设1：对于式（7）所描述的高空台空气起动系统，有界的期望输出信号

y d (t + 1)

存在有界的可行控制输入信号，在此控制输入信号的作用下，系统输出等于期望输出。

假设2：非线性函数

f (⋅)

关于高空台空气起动系统当前控制输入信号

u k (t)

的偏导数是连续的。

假设3：对于式（7）所描述的高空台空气起动系统，对任意的t和k满足广义李普希兹条件

Δ y * (t + 1)

≤ b

Δ u (t)

（8）

式中：

Δ u (t) = u k 1 (t) - u k 2 (t), u k 1 (t) ≠ u k 2 (t); Δ y * (t + 1) =

y k 1 * (t + 1) - y k 2 * (t + 1), k 1 ≠ k 2

；

b

是常数，式（8）成立表示有界的输入能量变化产生有界的输出能量变化。

若系统同时满足以上3个假设条件^［18］，则当

Δ u (t) ≠ 0

时，存在一个伪偏导数的向量，可建立紧格式线性化模型为

Δ y k * (t + 1) = φ (k t) Δ u k (t), φ (k t) ≤ b

(9)

式中：t是采样时刻；k是迭代轮次；

φ (k t)

表示伪偏导数。

Δ u k (t) = u k (t) - u k - 1 (t)

，表示相邻两轮迭代的控制差。同理，相邻两轮迭代的系统输出为

Δ y k * (t + 1) = y k * (t + 1) - y k - 1 * (t + 1)

。

3.2 无模型自适应迭代学习控制算法设计

确定空气起动系统的控制输入准则函数，如式（10）所示

J (u (t)) = y d (t + 1) - y k - 1 * (t + 1) 2 + λ u k (t) - u k - 1 (t) 2

(10)

式（10）中：

y d (t + 1)

、

y k - 1 * (t + 1)

分别为系统t+1时刻的空气起动系统目标压力和Smith估计器补偿压力；

u k (t)

、

u k - 1 (t)

分别为系统第k、k-1轮的主路控制阀开度。

式中的第1个平方项用于保证空气起动系统压力误差收敛，第2个平方项用于限制控制输入

u k (t)

的变化量，

λ

用于调节对控制输入变化量

u k (t)

的限制程度。

将式（9）带入式（10）中，对

u k (t)

求偏导并令其为0，即

∂ J / ∂ u k t = 0

，得到控制器如式（11）所示

u k (t) = u k - 1 (t) + ρ φ k (t) λ + φ k (t) 2 y d (t + 1) - y k - 1 * (t + 1)

(11)

式中：

ρ

为步长序列；

λ > 0

。

3.3 伪偏导数估计算法设计

确定空气起动系统的伪偏导数估计准则函数，如式（12）所示

J (φ k (t)) = (y k - 1 * (t + 1) - y k - 2 * (t + 1) - φ k (t) Δ u k - 1 (t)) 2 + μ (φ k (t) - φ k - 1 (t)) 2

（12）

式中：

y * k - 1 (t + 1)

、

y * k - 2 t + 1

分别为系统k-1、k-2轮迭代的空气涡轮进口实际压力；

μ

是参数估计变化量的惩罚因子，通过适当调整

μ

的数值，可以限制非线性系统的线性替代范围。

对式（12）中

ϕ k (t)

求偏导并令其等于0，即

∂ J / ∂ ϕ k t = 0

，得到如下伪偏导数估计算法

φ k (t) = φ k - 1 (t) + η Δ u k - 1 (t) μ + Δ u k - 1 (t) 2 Δ y k - 1 * (t + 1) - φ k - 1 (t) Δ u k - 1 (t)

（13）

式中：

η

为步长系数；

μ > 0

。

为有效防止伪偏导数估计对实际系统的估计出现大幅偏离，设计复位算法

φ k (t) = φ 0 (t), 如果 s g n φ k (t) ≠ s g n φ o (t), 或 φ k (t) ≤ ε, 或 Δ u k - 1 (t) ≤ ε

式中：

ε

为充分小的正数；

ϕ 0 (t)

是

ϕ k (t)

的初值；

s g n (⋅)

表示符号函数。

4 仿真分析

对基于Smith估计器的无模型自适应迭代学习控制设计进行仿真分析和有效性验证。压力数值通过归一化处理至（0~1）区间内。在仿真中，设计空气涡轮入口初始压力和温度分别为0（归一化）和288.15 K，气源初始压力和温度分别为1（归一化）和288.15 K。给定仿真时间区间为40 s，离散系统间隔设置为0.001 s，给定式（11）中的

ρ = 3.45

、

λ = 0.1

，式（13）中的

η = 0.2

、

μ = 0.1

、

ϕ 0 (t) = 2.2

。给定期望压力信号为阶跃信号

S t e p (t)

，其归一化后的表达式为

S t e p t = 0.525, t < 20 s 0.775, t ≥ 20 s

（14）

图5a表示5轮迭代下的系统压力输出变化曲线，随着迭代轮次增加，系统调节时间逐渐缩小，系统动态性能得到明显改善。图5b表示30~40 s系统最大静态误差随着迭代轮次变化曲线，由于前2轮迭代在20 s前未收敛，因此分析30-40s区间内的静态误差，由图中曲线趋势可知，随着迭代轮次增加系统最大静态误差明显减少。由图5c和图5d可知，系统延迟时间超过1 s，在两次阶跃信号输入下，Smith估计器能有效减少系统延迟导致的超调现象，且调节时间也得到明显减少。

显示原图|下载原图ZIP|生成PPT

图5 仿真结果分析图

5 结论

本文提出了一种基于Smith估计的空气起动系统无模型自适应迭代学习控制方法，实现了对空气起动系统的快速精确控制。从仿真结果可知，对于大延迟系统，Smith估计器能有效增强系统的动态调节性能，无模型自适应迭代学习能让系统在较短的时间内，实现系统的跟踪。在后续的研究中，会考虑加入旁路控制阀，实现高空台空气起动系统的双阀控制，进一步提高系统的调节性能。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	熊荆江.某航空发动机高空模拟试车台供气系统设计研究［D］.长沙：湖南大学，2011.

2	范泽兵，胡杨，吴锋，等.航空发动机高空模拟试车台架参数化设计研究［J］.燃气涡轮试验与研究，2018，31（3）：53-57.

3	谌昱，陈龙，田野.某型直升机空气起动系统管路关键参数研究［J］.直升机技术，2022，29（2）：16-22，27.

4	雷勇，李辉，石小江.航空发动机空气起动系统的前馈-反馈复合控制［J］.机电工程，2011，28（5）：586-589.

5	朱美印，王曦，但志宏，等.高空台进气控制系统压力PI增益调度控制研究［J］.推进技术，2019，40（4）：902-910.

6	赵涌，侯敏杰，黄振南，等.航空发动机高空模拟试验飞行高度模糊PID控制系统［J］.机电工程，2010，27（1）：68-71.

7	钱秋朦，但志宏，张松，等.航空发动机过渡态试验进气压力线性自抗扰控制方法［J］.航空动力学报，2019，34（10）：2271-2279.

8	Zhu P P， Jin S T， Bu X H，et al.Improved model⁃free adaptive control for MIMO nonlinear systems with event⁃triggered transmission scheme and quantization［J］.IEEE Transactions on Cybernetics，2023，53（9）：5867-5880.

9	Chi R H， Hou Z S， Wang D W，et al.An optimal terminal iterative learning control approach for nonlinear discrete⁃time systems［J］.Control Theory & Applications，2012，29（8）：1025-1030.

10	毛宇涵，李来春，张亮，等.基于Smith预估控制和遗传算法优化的燃油蒸汽锅炉燃烧控制［J］.热能动力工程，2023，38（3）：105-111.

11	裴希同，朱美印，张松，等.一种特种流量特性计算的经验公式迭代方法［J］.燃气涡轮试验与研究，2016，29（5）：35-39.

12	裴希同，张松，但志宏，等.高空台飞行环境模拟系统数字建模与仿真研究［J］.推进技术，2019，40（5）：1144-1152.

13	朱美印，裴希同，张松，等.一种轮盘式特种调节阀流量特性的修正算法［J］.燃气涡轮试验与研究，2016，29（5）：40-45.

14	朱美印，张松，但志宏，等.一种大口径蝶阀流量特性的坐标定位回归算法［J］.燃气涡轮试验与研究，2017，30（4）：39-44.

15	沈维道，童钧耕.工程热力学［M］.北京：高等教育出版社，2016.

16	毛宇涵，李来春，张亮，等.基于Smith预估控制和遗传算法优化的燃油蒸汽锅炉燃烧控制［J］.热能动力工程，2023，38（3）：105-111.

17	陆燕，杜继宏，李春文.延迟时间未知的时延系统神经网络补偿控制［J］.清华大学学报（自然科学版），1998，38（9）：68-70.

18	Chi R H， Yu H， Hou Z S.Data⁃driven iterative learning control for discrete⁃time systems［M］.Singapore：Springer Nature Singapore，2022.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 空气起动系统建模

1.1 空气起动系统工作原理

图1 空气起动系统组成结构图

1.2 主路/旁路控制阀建模

表1 阀门流量系数特性表

1.3 管道容腔建模

图2 空气起动系统简化图

图3 双通容腔图

2 Smith估计器设计

图4 基于Smith估计的空气起动系统无模型自适应迭代学习控制框图

3 无模型自适应迭代学习控制器设计

3.1 高空台空气起动系统动态线性化

3.2 无模型自适应迭代学习控制算法设计

3.3 伪偏导数估计算法设计

4 仿真分析

图5 仿真结果分析图

5 结论

参考文献