旅行商问题（travelling salesman problem，TSP）是组合优化中典型的NP-hard问题［1］，在实际生活中有广泛的应用，如：电网规划、车辆调度和机器人控制等［2-3］。研究TSP问题的求解具有重要的意义。目前求解TSP问题的算法主要分为精确算法和启发式算法两类。精确算法有分支定界、线性规划和动态规划法等［4-5］。精确算法可求得小规模TSP问题最优解，在处理大规模问题时，很难在有限时间内得到问题的最优解。随着问题规模的增大，许多研究［6-8］多采用启发式算法进行求解。启发式算法包括蚁群算法（ant colony optimization，ACO）、遗传算法（genetic algorithm，GA）、模拟退火算法（simulated annealing， SA）以及禁忌搜索算法等。TS作为一种启发式算法，在求解函数优化问题中表现出优良的性能［9-11］，但同时也存在对初始解依赖较强的缺陷，好的初始解对TS算法求解有较大的帮助。
1 TSP问题数学模型
TSP问题可描述为：假设有一个旅行商要访问n座城市，各城市间距离已知，路径限制是每个城市只能被访问一次，旅行商从初始城市出发，在遍历所有城市后，最后返回初始城市，求最短路径的巡回方案。
TSP问题数学模型［14］如式（1） 所示
式中：g（x）为路径总长度；d（yi，yi +1）为第i个访问城市到第i+1个访问城市的距离；y=（y 1，y 2，…，yn ）表示访问城市的顺序；n为访问城市个数；1，2，…，n表示访问城市序号。
TSP问题按其距离矩阵分为对称和非对称性TSP问题，本文研究对称性TSP问题。
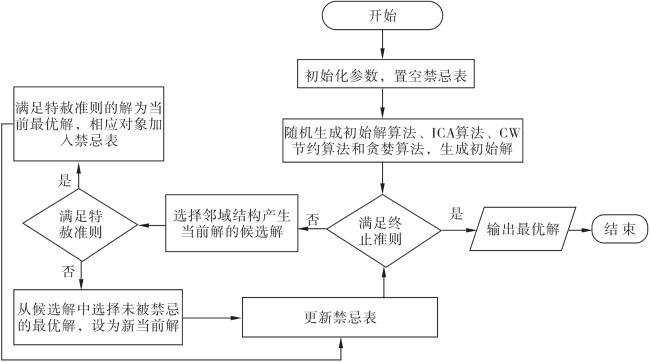
2 改进的禁忌搜索算法
TS算法是由美国科罗拉大学Fred Glover教授在1986年首次提出［15］。TS算法通过引入相应的禁忌表来避免重复搜索，并对禁忌区域中的一些优良状态进行特赦，避免算法陷入局部最优，是一种全局迭代寻优的算法。
TS算法具备强大的局部搜索能力和记忆功能，但其对初始解的依赖性较强，较好的初始解可使算法快速找到最优解。为降低初始解对算法的影响，提高TS算法的计算效率，本文比较了随机生成初始解算法、ICA算法、CW节约算法和贪婪算法4种方法生成初始解，将其中最好的初始解作为TS算法的初始解进行迭代，进而寻求最优解。
ICA算法［16］求解TSP问题的基本思想是先随机生成路径，形成一个Hamilton圈，随机交换Hamilton圈内除起始点和终止点外的两个点位置，若交换后的路径总长度小于交换前的路径总长度，接受此次交换，成功交换次数加1，更新最短路径，直至成功交换次数达到设置的改良次数，结束搜索。ICA算法搜索随机性不高，较难得到全局最优解，易陷入局部最优。因此，该算法常用于构造初始解，并结合相关启发式算法求解TSP问题。
CW节约算法是Clark等17］提出的一种解决车辆路径问题较为有效的启发式算法，其求解TSP问题基本原理如下：生成一条只包含起始点和终止点的初始路径，从所有需要访问城市中随机选择一个城市插入到初始路径中，计算剩余城市在所有可能插入位置的节约值，将节约值从大到小降序排列，把节约值最大的城市插入到最佳可行位置，直至车辆经过所有需要访问的城市后返回出发城市。
贪婪算法［18］生成TSP问题初始解的方法为从第一个城市出发，每次在没有到达的城市中选择距离最近的一个城市访问，依次进行，直至经过所有访问城市，最后返回出发城市。
根据TSP问题的特点，本文设计了3种邻域结构，从中选择计算效果最佳的邻域结构。
Insert邻域：在生成的初始城市序列中随机选择两个不同位置a和b，将位置a对应的城市插入位置b，记为Insert（a， b）；如生成初始城市序列R=［1， 5， 2， 4， 3， 6， 7］，随机选取的城市为［5， 3］，则Insert邻域变换如图1 所示。
Swap邻域：在生成的初始城市序列中随机选择两个不同位置a和b，将位置a和b对应的城市交换，记为Swap（a， b）；如生成初始城市序列R=［1， 5， 2， 4， 3， 6， 7］，随机选取的城市为［5， 3］，则Swap邻域变换如图2 所示。
2-opt邻域：在生成的初始城市序列中随机选择两个不同位置a和b，将位置a和b对应的城市交换，将位置a和b对应城市之间的所有城市进行倒序排列；如生成初始城市序列R=［1， 5， 2， 4， 3， 6， 7］，随机选取城市为［5， 3］，则2-opt邻域变换如图3 所示。
改进的TS算法求解TSP的步骤如下：
步骤1：设置算法基本参数，即禁忌表长度为TL，候选解个数为K，最大迭代次数为T max；
步骤2：用随机生成初始解算法、ICA算法、CW算法和贪婪算法生成初始解，选择其中最优的初始解，判断它是否满足终止条件：若满足，则输出最优解，算法结束；否则，转入步骤3；
步骤3：用Insert邻域、Swap邻域和2-opt邻域结构产生邻域解，选择其中计算结果最优的邻域结构，在它生成的若干邻域解中挑选K个候选解，计算目标值，选取结果较好的候选解；
步骤4：判断候选解是否满足特赦准则：若满足，特赦候选解，更新当前最优解，将其加入禁忌表，更新禁忌表；否则，选择候选解中未被禁忌的最优解作为当前最优解，更新禁忌表；
步骤5：重复步骤3和步骤4，直至满足程序终止条件，结束搜索。
改进的TS算法流程图见图4 所示。
3 仿真实验
仿真实验分别采用了文献［12］、［ 13］中的算例与标准TSPLIB数据库中的算例，将本文算法的计算结果与算例中的实验结果进行比较。本文算法用Python实现，在Window10操作系统，处理器为Inter（R）Core（TM）i7-7700（2.80Ghz），8 GB内存的电脑上运行。
文献［12］中的城市数为31，城市分布散点如图5 所示。
3.1 本文算法参数设置
本文比较了在不同禁忌长度和候选集规模组合下的最优解结果，并确定了禁忌长度和候选集规模的最优参数。
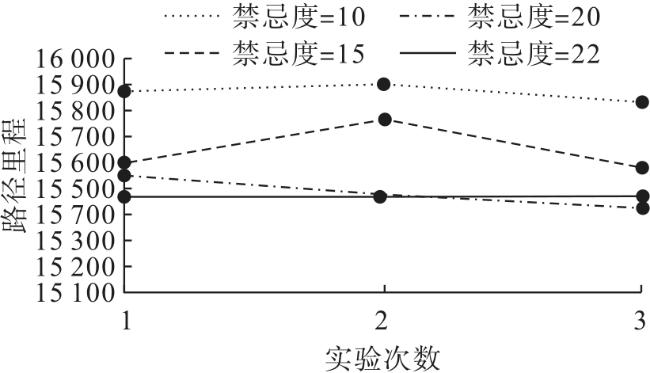
3.1.1 禁忌长度的选择
禁忌长度是禁忌搜索算法中的一个关键参数，作为放置在禁忌表中对象的禁忌周期，进行一次迭代，周期减少一次，直至周期为0时解除禁忌。禁忌长度的选择影响最终最优解的结果。文献［12］的算例采用随机生成初始解算法，设置K=200、N=100，采用2-opt邻域变换。本文算法的禁忌长度分别为10、15、20、22，在不同禁忌长度下，重复运行3次程序，AVG为3次计算结果平均值，具体计算结果如表1 所示，计算结果如图6 所示。
从图6 可知，在其他参数固定的情况下，禁忌长度从10增大到20，计算结果逐渐减小；禁忌长度从20增大到22，计算结果相近。
从表1 可得，当TL=22时，计算结果平均值最小，最短路径平均长度为15 466。因此，在其他参数固定条件下，本文取TL=22。
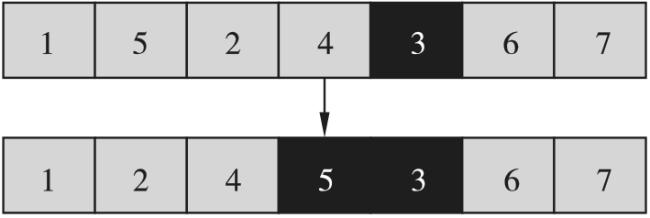
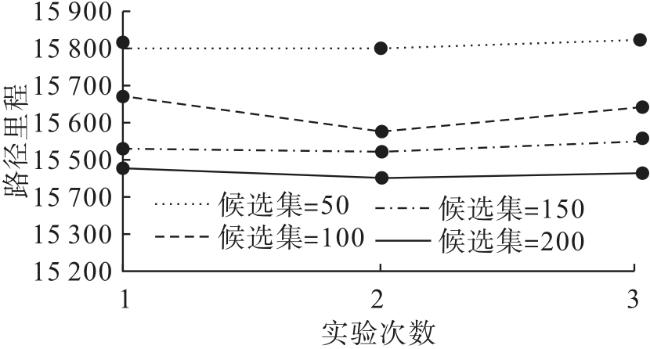
3.1.2 候选集选择
候选集从邻域解中产生，随机选择几个邻域解或选表现较好的解作为候选解。本实验设置TL=22、N=100，采用2-opt邻域变换，设置候选解集个数分别为50、100、150和200。在不同候选解集下，重复运行3次程序，AVG为3次计算结果平均值，具体计算结果如表2 和图7 所示。
从表2 可知，当K=200时，计算得到路径最短距离平均值最小，最短路径平均长度为15 466。因此，在其他参数固定条件下，本文将候选解的数量设置为200。由图7 可知，在其他参数固定时，候选集数量从50增大到200，所得最短距离逐渐减小。
3.2 初始解选择
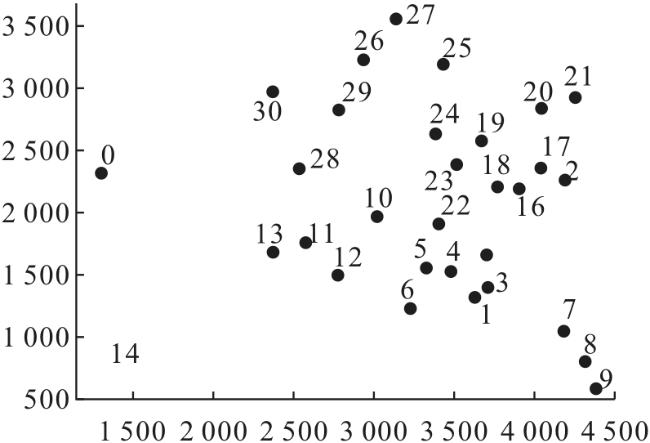
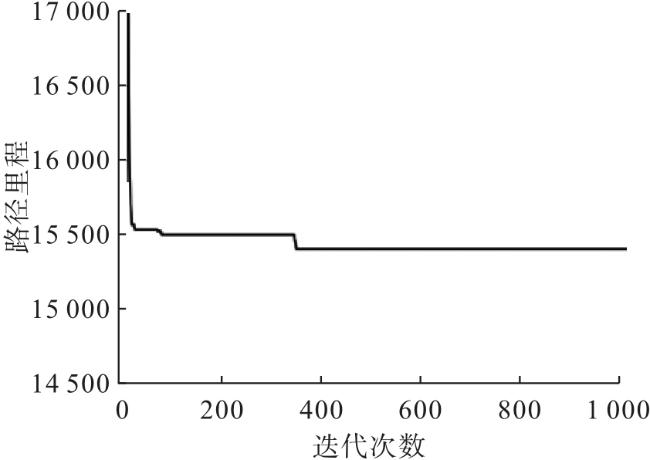
3.2.1 文献［13］算例
文献［13］中有21个客户的位置坐标数据，本文算法设置参数TL=10，N=100，K=30，邻域结构为2-opt，改良次数T=20，将不同算法得到初始解代入TS算法，重复运行5次实验，其中AVG为5次计算结果的平均值，计算结果如表3 所示。
表3 文献［13］算例实验结果 |
| 算法 | 1 | 2 | 3 | 4 | 5 | AVG |
|---|---|---|---|---|---|---|
| 随机生成初始解算法 | 274 | 262 | 271 | 274 | 274 | 271 |
| ICA算法 | 268 | 262 | 268 | 274 | 272 | 268 |
| CW节约算法 | 263 | 269 | 265 | 271 | 262 | 266 |
| 贪婪算法 | 268 | 269 | 262 | 263 | 262 | 264 |
从表3 可知，贪婪算法计算结果平均值最小，最短路径平均长度为264.8，相较随机生成初始解算法、ICA算法和CW节约算法最短路径平均长度分别减少5.0、4.0和1.2。
3.2.2 文献［12］算例
实验采用文献［12］中的31个城市数据坐标，设置参数TL=22、N=100、K=200、T=20，邻域结构为2-opt，将不同算法得到初始解代入TS算法，重复运行5次实验，其中AVG为5次计算结果的平均值，计算结果如表4 所示。
表4 文献［12］算例实验结果 |
| 算法 | 1 | 2 | 3 | 4 | 5 | AVG |
|---|---|---|---|---|---|---|
| 随机生成初始解算法 | 15 551 | 15 603 | 15 398 | 15 475 | 15 525 | 15 510 |
| ICA算法 | 15 433 | 15 641 | 15 428 | 15 482 | 15 508 | 15 498 |
| CW节约算法 | 15 559 | 15 594 | 15 382 | 15 455 | 15 554 | 15 508 |
| 贪婪算法 | 15 410 | 15 475 | 15 387 | 15 505 | 15 447 | 15 444 |
从表4 可知，贪婪算法计算结果平均值最小，最短路径平均长度为15 444，相较随机生成初始解算法、ICA算法和CW节约算法最短路径平均长度分别减少66、64和54。因此，本文选择贪婪算法作为算法初始解。
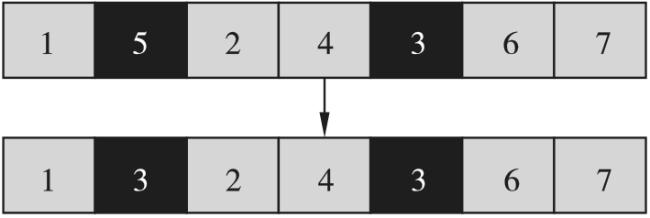
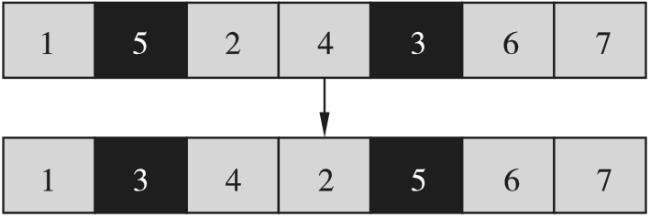
3.3 邻域结构
为增加解的多样性，本文算法提出基于变邻域搜索的干扰机制，比较了Insert邻域、Swap邻域和2-opt邻域求解文献［12］中算例的近优解结果。设置TL=22、N=100、K=200，在不同邻域结构下，重复运行5次实验，AVG为5次计算结果平均值，计算结果如表5 所示。
表5 不同邻域算法结果 |
| 邻域 | 1 | 2 | 3 | 4 | 5 | AVG |
|---|---|---|---|---|---|---|
| Insert | 15 536 | 15 501 | 15 495 | 15 528 | 15 498 | 15 511 |
| Swap | 15 429 | 15 447 | 15 449 | 15 398 | 15 474 | 15 439 |
| 2-opt | 15 398 | 15 410 | 15 457 | 15 472 | 15 399 | 15 427 |
从表5 可知，当邻域结构为2-opt时，计算结果平均值最小，最短路径平均长度为15 427，相较采用Insert邻域和Swap邻域所得最短路径平均长度分别减少84和12。因此，本文选择2-opt邻域结构。
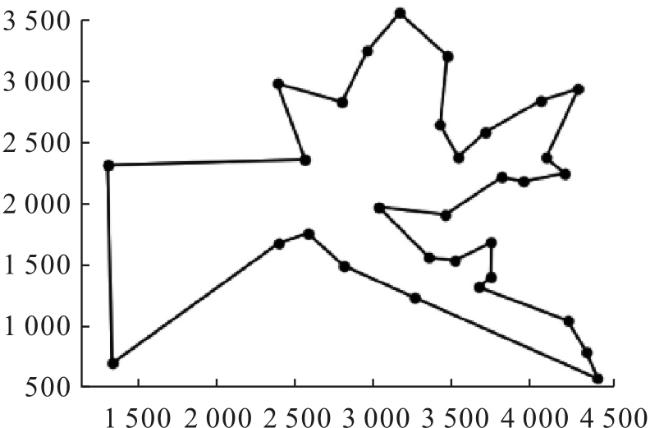
3.4 算例比较
本文采用文献［12］数据和算法、TSPLIB数据库中算例和结果来验证本文算法的有效性。
3.4.1 文献［12］算法与本文算法计算结果比较
偏差率
表6 文献［12］与本文算法计算结果比较 |
| 迭代次数 | 实验次数 | a | b | 偏差率/% |
|---|---|---|---|---|
| 100 | 1 | 16 905 | 15 483 | 9.18 |
| 2 | 17 609 | 15 498 | 13.62 | |
| 3 | 17 703 | 15 536 | 13.95 | |
| 4 | 17 152 | 15 619 | 9.81 | |
| 5 | 17 394 | 15 520 | 12.07 | |
| 500 | 1 | 16 526 | 15 464 | 6.87 |
| 2 | 16 587 | 15 387 | 7.80 | |
| 3 | 16 550 | 15 410 | 7.40 | |
| 4 | 16 852 | 15 422 | 9.27 | |
| 5 | 17 178 | 15 399 | 11.55 | |
| 1000 | 1 | 15 800 | 15 433 | 2.38 |
| 2 | 16 037 | 15 398 | 4.15 | |
| 3 | 15 382 | 15 382 | 0 | |
| 4 | 16 006 | 15 410 | 3.87 | |
| 5 | 15 824 | 15 382 | 2.87 |
3.4.2 TSPLIB数据库算例与本文算法计算结果的比较
本文采用TSPLIB数据库中的Dantzig42、Berlin52、St70进行算例测试，重复运行5次实验，其中n为城市数量，AVG为5次计算结果平均值，opt为本文算法最优值，ref为TSPLIB参考值，计算结果如表7 所示。参考值为TSPLIB数据库中相应最优值，偏差率计算方法如式（3） 所示
表7 TSPLIB最优解与本文算法实验结果比较 |
| 算例 | n | AVG | opt | ref | 偏差率/% |
|---|---|---|---|---|---|
| Dantzig42 | 42 | 705 | 699 | 699 | 0 |
| Berlin52 | 52 | 7 694 | 7 656 | 7 542 | 1.51 |
| St70 | 70 | 699 | 692 | 675 | 2.52 |
从表7 可知，本文算法计算Dantzig42实例的最优解达到TSLIB标准库的最优解。Berlin52和St70实例的最优解与TSPLIB标准库中的最优解相比，偏差率在3%以内，本文算法在小规模案例下，计算结果较为理想。
4 结论
本文针对TSP问题的特点，通过随机生成初始解算法、ICA算法、CW节约算法和贪婪算法生成初始解，选择计算结果最优的贪婪算法对TS算法的初始解进行优化，提出一种改进的禁忌搜索算法。仿真实验中，通过不同情况下参数比较，确定禁忌长度和候选集的最优参数。仿真实验结果表明：相较文献［12］中算法的最优解，本文算法的最优解更接近全局最优解，说明本文算法能够有效解决TSP问题。在与TSPLIB标准库算例比较中，本文算法在小规模算例中计算结果与TSPLB标准库参考值之间的偏差率不超过3%，验证了本文算法求解TSP问题的有效性和可行性。