1 随机变分不等式的转化
2 随机变分不等式的二阶微分方程方法
3 数值实验
表1 总结了运用二阶微分方程系统(11)求解例1的数值结果。图1中给出了从所给的初始点出发,二阶微分方程系统(11)求解例1所得到的解的轨迹 。 |
| 时间/ms | x (t) | 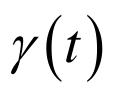 | 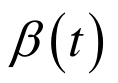 |
|---|---|---|---|
| 50 |  | 0.5 | 1 |
| 100 |  | 0.25 | 1 |
| 150 |  | 0.167 | 1 |


|
庄慧婷(1999-),女,辽宁营口人,硕士研究生,主要研究方向:运筹学与控制论,E-mail: zhuanghuiting228@163.com |
|
王莉(1978-),女,辽宁葫芦岛人,副教授,博士,主要研究方向:运筹学与控制论,E-mail:liwang211@163.com。 |
收稿日期: 2023-03-31
网络出版日期: 2023-11-09
基金资助
国家自然科学基金(11901422)
Second-order differential equation method for solving stochastic variational inequality
Received date: 2023-03-31
Online published: 2023-11-09
运用具有正黏性阻尼系数和时间尺度系数的二阶微分方程系统来求解随机变分不等式问题(stochastic variational inequality problem,SVIP)。首先,应用互补函数和样本均值近似(sample average approximation, SAA)方法对原始问题进行等价转换,即将随机变分不等式问题转化为一个方程组,在此基础上建立具有正黏性阻尼系数 和时间尺度系数 的二阶微分方程系统;其次,研究了该二阶微分方程系统轨迹的收敛性和收敛速率;最后,给出两个数值实验说明该二阶微分方程系统求解随机变分不等式问题的有效性。
庄慧婷 , 王莉 , 孙菊贺 , 贾丹娜 , 袁艳红 . 随机变分不等式的二阶微分方程方法[J]. 沈阳航空航天大学学报, 2023 , 40(4) : 88 -96 . DOI: 10.3969/j.issn.2095-1248.2023.04.012
A system of second-order differential equation with positive viscous damping coefficients and time-scale coefficients was applied to solve the stochastic variational inequality problem (SVIP). Firstly, the complementary function and the sample average approximation (SAA) method were applied to equate the original problem, and the stochastic variational inequality problem was transformed into a system of equations. Based on this, a second-order differential equation system with positive viscous damping coefficients and time-scale coefficients was established. Secondly, the convergence and convergence rate of the trajectory of the second-order differential equation system were obtained. Finally, two numerical experiments were presented to demonstrate the effectiveness of the second-order differential equation system in solving stochastic variational inequality problems.
表1 总结了运用二阶微分方程系统(11)求解例1的数值结果。图1中给出了从所给的初始点出发,二阶微分方程系统(11)求解例1所得到的解的轨迹 。 |
| 时间/ms | x (t) | 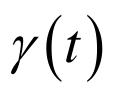 | 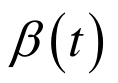 |
|---|---|---|---|
| 50 |  | 0.5 | 1 |
| 100 |  | 0.25 | 1 |
| 150 |  | 0.167 | 1 |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
杨振平.随机变分不等式问题及其在天然气市场中的应用研究[D].上海:上海大学,2019.
|
| 8 |
陈琦琼.不确定变分不等式及其在非合作博弈中的应用[D].南京:南京理工大学,2018.
|
| 9 |
|
| 10 |
R.Tyrrell Rockafellar and Roger J-B Wets.Stochastic variational inequalities:single-stage to multistage [J].Mathematical Programming,2017,165(1):331-360.
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
/
| 〈 |
|
〉 |