基于1D-CNN的齿轮3D振动信号故障诊断方法

蒋丽英; 刘桂金; 崔建国; 杜文友; 于明月

doi:10.3969/j.issn.2095-1248.2023.04.004

沈阳航空航天大学学报 >

2023 , Vol. 40 >Issue 4: 25 - 31

DOI: https://doi.org/10.3969/j.issn.2095-1248.2023.04.004

信息科学与工程

基于1D-CNN的齿轮3D振动信号故障诊断方法

蒋丽英 ,
刘桂金 ,
崔建国 ,
杜文友 ,
于明月

展开

沈阳航空航天大学自动化学院，沈阳 110136

蒋丽英( 1976-) ,女,辽宁沈阳人,副教授,博士,主要研究方向: 旋转机械系统故障特征提取、故障检测和故障诊断, E-mail: jlylcb01@ 163. com。

收稿日期: 2022-10-14

网络出版日期: 2023-11-09

基金资助

国家自然科学基金(61903262)

辽宁省教育厅项目(JYT2020021)

收起

Fault diagnosis method for gear 3D vibration signal based on 1D-CNN

JIANG Liying ,
LIU Guijin ,
CUI Jianguo ,
DU Wenyou ,
YU Mingyue

Expand

College of Automation，Shenyang Aerospace University，Shenyang 110136，China

Received date: 2022-10-14

Online published: 2023-11-09

Fold

摘要

为了解决从齿轮一维振动信号提取故障特征不全面的问题，提出一种基于一维卷积神经网络（one-dimensional convolutional neural network，1D-CNN）的齿轮3D振动信号故障诊断新方法。首先，提取原始三维振动信号各维的时域特征；其次，利用一维卷积神经网络（1D-CNN）模型进行特征选择；最后，将选择后的特征进行重组，重组特征作为1D-CNN故障诊断模型的输入实现故障分类操作。结果表明，利用提出的故障诊断方法，诊断准确率显著提高。模型的结构简单，训练速度快，能够快速实现故障诊断。

关键词： 三维振动信号; 时域特征; 一维卷积神经网络; 故障诊断; 齿轮

本文引用格式

蒋丽英 , 刘桂金 , 崔建国 , 杜文友 , 于明月 . 基于1D-CNN的齿轮3D振动信号故障诊断方法[J]. 沈阳航空航天大学学报, 2023 , 40(4) : 25 -31 . DOI: 10.3969/j.issn.2095-1248.2023.04.004

Abstract

In order to solve the problem of incomplete fault feature extraction from gear one-dimensional vibration signal，a new fault diagnosis method of gear 3D vibration signal based on one-dimensional convolution neural network was proposed.Firstly，the time domain features of each dimension of the original three-dimensional vibration signal were extracted；Secondly，the one-dimensional convolutional neural network model was used for feature selection；Finally，the selected features were reorganized，and the reorganized features were used as the input of 1D-CNN fault diagnosis model to achieve fault classification operation.The results show that the accuracy of diagnosis is remarkably improved by using the proposed fault diagnosis method.Moreover，the structure of the model is simple，the training speed is fast，and the fault diagnosis can be achieved quickly.

Key words： three-dimensional vibration signal; time domain features; one-dimensional convolutional neural network; fault diagnosis; gear

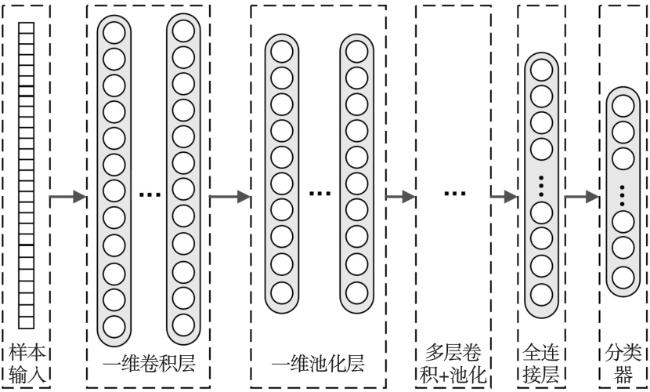
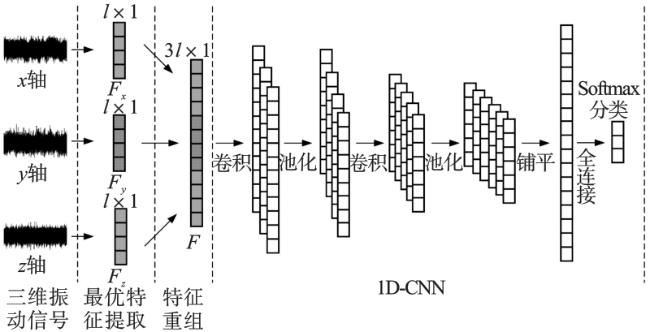
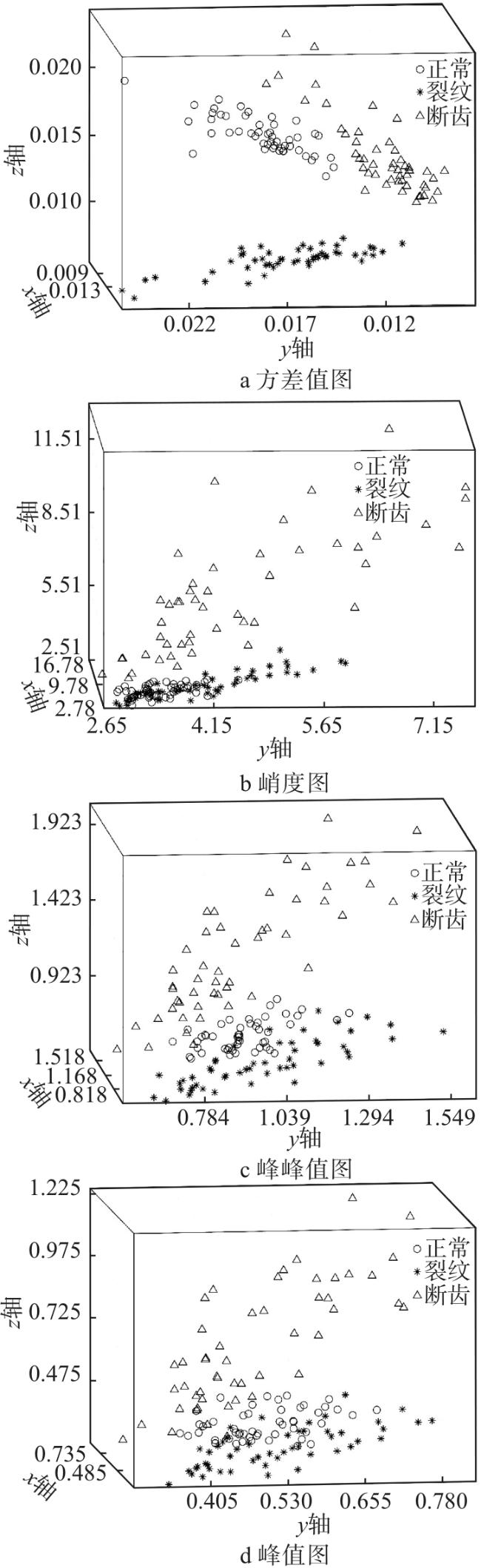
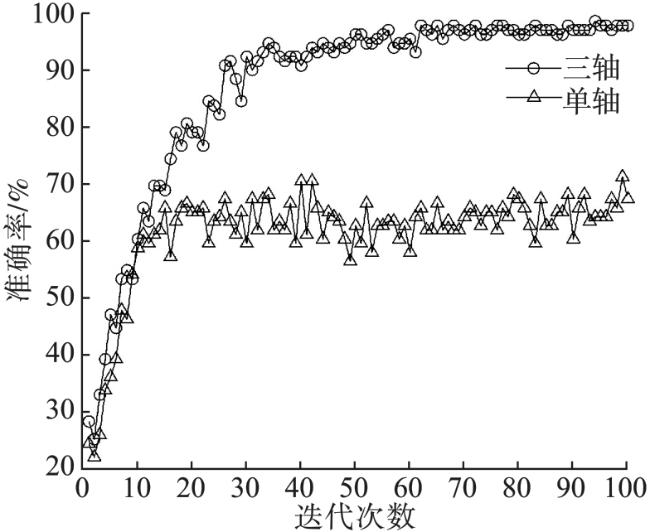
齿轮是工程设备运行重要部件之一，若齿轮发生故障，轻则导致工程设备运行不正常，重则威胁到工作人员的人身安全。因此，对齿轮的故障诊断方法进行研究是十分必要的^［1］。但是齿轮发生的故障通常难以直接监测，通过对其产生的振动信号进行分析，进而判断发生故障的类型是一种有效的方法。

对振动信号的处理主要包括特征提取、特征选择^［2］、利用选择后的特征进行故障分类。特征提取的目的是提取原始振动信号中与故障状态有关的特征。通常采用一些基于信号处理的方法，例如小波变换^［3］、快速傅里叶变换^［4］、经验模态分解^［5］等特征提取完成后，需要对提取的特征进行筛选，目的是将故障信息不明显的特征去除，以此来进一步减少特征的数目。通常采用的方法有主成分分析法^［6］，独立分量分析法^［7］等。最后一个阶段是将筛选后的特征作为网络模型的输入，通过训练网络模型完成故障的模式识别。

近年来，随着大数据时代的到来，深度学习被广泛应用于机械部件故障诊断领域。卷积神经网络作为深度学习中的一种，其优势在于强大的特征自学习性能，能够避免人为因素的干扰，实现故障分类。目前，已有一些研究者将CNN应用到齿轮箱故障诊断领域。Chen等^［8］通过将振动信号的特征统计图输入CNN，实现了故障分类。吴春志等^［9］直接将原始振动信号作为1D-CNN的输入，证明了1D-CNN模型对单一和复合故障的诊断性能均优于传统诊断方法。这种方法虽然能够简化诊断流程，但是原始振动信号中存在的大量干扰信息会对诊断结果造成不良影响。

三轴振动传感器在大型旋转机械的在线监测与故障诊断中应用越来越广泛，3D振动信号的采集工作也变得简单易行。因此，寻找能够有效利用3D振动信号实现齿轮故障诊断的方法是当前亟待解决的问题。为此，本文提出了一种基于1D-CNN的齿轮3D振动信号故障诊断方法。首先，采用1D-CNN对3D振动信号时域特征进行选择；然后，根据获得的最优时域特征参数集提取3D振动信号的相关特征，并将3D特征数据横向排列重构成1D特征向量；最后，利用1D-CNN实现对齿轮的故障诊断。通过实验验证，与基于1D振动信号的诊断结果相比，诊断准确率得到提高，并对本文的网络模型在不同工况的泛化性能进行了分析。

1 振动信号的时域特征

作为旋转机械中常用的部件，齿轮长时间处于运转状态，容易引起点蚀、断齿及裂纹等类型的故障。由于互动效应，甚至会引起部件之间的复合型故障，导致机械系统局部陷入瘫痪。因此，对齿轮的运行状态进行监测十分必要。

在复杂的工作条件下，齿轮振动信号具有非线性、非平稳的特点^［10］，该特点会使故障信息不明显，无法反映出齿轮的运行状态。齿轮的振动信号一般为与时间相关的序列，因此，采用时域分析，通过提取振动信号的时域特征参数精准地反映齿轮的运行状态。时域特征分为有量纲和无量纲两种^［11］。其中，有量纲特征能够有效跟踪齿轮的运行状态，但是易受到外界条件的干扰。相比较而言，无量纲特征能够排除外界因素的干扰，更加稳定地跟踪齿轮的运行状态。因此，为了更全面地表征齿轮的运行状态，本文将有量纲与无量纲特征组合使用。

2 一维卷积神经网络

卷积神经网络具备强大的特征自提取能力，能够更加深入地挖掘时域特征中表征齿轮工作状态的深层次信息，特征的利用率更高。因此，对特征进行分类的效果进一步得到提高。CNN通常分为1D-CNN、2D-CNN和3D-CNN。1D-CNN主要用于处理序列类的数据，2D-CNN常应用于识别图像类文件，3D-CNN主要用于医学领域内的图像识别^［12］。1D-CNN模型一般由卷积层、池化层、全连接层等组成^［13］，网络结构如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 1D-CNN模型网络结构图

卷积层通过卷积核权值共享对输入进行卷积运算^［14］。卷积运算可以表示为

y i (l + 1) (j) = K i l · X l (j) + b i l

（1）

式中：

K i l

和

b i l

为第

l

层中第

i

个卷积核的权重和偏差；

X l (j)

为第

l

层中第

j

个局部区域；

y i (l + 1) (j)

为第

l + 1

层第

i

个卷积核运算结果中第

j

个神经元的输入。激活函数选择修正线性单元ReLU，其采用单侧抑制的原则进行输出，可以增加网络的稀疏性，进而提高网络的计算效率。

卷积层之后一般是池化层，应用较多的是最大池化^［15］，该方式能够保留特征图中的最大局部特征。其函数表达式为

P i l + 1 (j) = m a x (j - 1) W + 1 ≤ t ≤ j W {q i l (t)}

（2）

式中：

q i l (t)

代表第l层的第i个特征矢量中第t个神经元的值，其中，

t ∈ [(j - 1) W + 1, j W]

；W表示池化区域的大小；

P i l + 1 (j)

表示池化运算后第l+1层神经元对应的值。

全连接层通常位于池化层之后，将池化层最后一层的输出进行首尾连接后转化为一维向量^［16］。之后利用Soft-max分类器执行故障分类的任务，其运算过程如式（3）所示

f (z j) = e z j ∑ k n e z k

（3）

式中：j代表k类中的某一类别，该类别的值用

z j

表示。

3 面向3D振动信号的1D-CNN故障诊断模型

3.1 基于1D-CNN的时域特征参数选择

在众多的时域特征参数中，并不是每个特征都能有效地表征齿轮的故障状态。因此，本文采用1D-CNN网络，以平均故障诊断率作为筛选准则，对时域特征进行筛选。具体步骤如下：

步骤1：使用三轴振动加速度传感器采集P种已知故障（包含正常齿轮）的振动信号，其中每种故障的3D振动信号记为 q=｛

s x (t)

，

s y (t)

，

s z (t)

｝，下标x、y、z分别表示3D振动信号的x轴（径向）、y轴（轴向）和z轴（周向）。设置样本长度为m，每种故障的样本数为

N p

（p=1，2，…，P），构建样本数据。显然，样本 q 为m×3的数据。

步骤2：确定时域特征参数集F =｛

F j

｝，j=1，2，…，J；设置1D-CNN网络结构参数，并令j=1。

步骤3：分别对P种样本数据提取第j种时域特征，构建特征集

X p j ∈ R N p × 3

。其中，

X p j

的第i行为、第p种故障的第

i

个样本的时域特征值

f x j, f y j, f z j p i

。

步骤4：将第j种时域特征的特征集｛

X p j

｝（p=1，2，…，P）分为训练集和测试集。训练集用来训练第j种时域特征的1D-CNN模型；测试集用来计算1D-CNN模型的故障诊断准确率。

步骤5：若平均故障诊断准确率大于给定阈值σ %，则该时域特征参数

F j

为最优参数，并加入最优参数集F ^*。

步骤6：令j=j+1，重复步骤3~5，直到特征参数

F j

被筛选完为止。

3.2 基于1D-CNN的故障诊断方法

本文提出的基于1D-CNN的齿轮3D振动信号故障诊断流程如图2所示。该方法的具体步骤如下：

显示原图|下载原图ZIP|生成PPT

图2 面向3D振动信号的1D-CNN故障诊断模型

步骤1：最优特征提取。按照3.1节确定的包含l个时域特征参数的最优参数集F ^*，对P种故障样本数据提取最优特征。对于样本

x ∈ R m × 3

，按3个轴记为

F x

、

F y

、

F z

、对x、y和z轴长度为m的振动信号提取时域特征。

步骤2：特征重组。将每个样本的最优特征向量按行的方向重组为一维特征向量

F ∈ R 3 l × 1

，即

F = F x T, F y T, F z T T

，如图2所示。

步骤3：设置1D-CNN故障诊断模型结构参数，输入层为重组后的特征向量

F

，输出层为P种故障类别。将样本数据分为训练集和测试集，按步骤1对训练集和测试集提取最优特征，按步骤2分别对训练集和测试集的最优特征进行重组，从而构建训练特征集和测试特征集。训练特征集用来训练神经网络，得到1D-CNN故障诊断模型。

步骤4：测试时，利用训练好的1D-CNN故障模型对测试特征集进行分类，最后用故障诊断准确率评价所提出方法的性能。

4 模型验证

4.1 故障模拟试验

本文的实验数据是用江苏千鹏QPZZ - II型旋转机械故障模拟实验台测得。该实验台如图3所示，齿轮箱由55齿的主动齿轮和75齿的从动齿轮组成。采用电子放电的方法将裂纹和断齿故障分别引入从动齿轮。齿轮箱顶部安装B&K 4056三轴加速度传感器，以获取齿轮径向（x轴）、轴向（y轴）和周向（z轴）的三轴振动信号。将径向（x轴）的振动信号作为单轴振动信号。

显示原图|下载原图ZIP|生成PPT

图3 QPZZ-II旋转机械故障模拟实验台

本实验台的数据采样频率设置为5kHz。将齿轮3种工作状态设置为1、2、3这3种标签。每种工作状态中选取150组样本数据，每组样本包括1 024个采样点。将150组样本按照1：2分成训练集样本和测试集样本，即选取其中50组样本作为训练集，100组样本作为测试集。

4.2 特征选取

本文从原始3D振动中提取了10个时域特征参数，利用1D-CNN模型对每个特征参数进行诊断分类。计算齿轮3种工作状态的平均故障诊断准确率，按照从高到低的顺序排列，如表1所示。

表1 时域特征诊断准确率

编号	特征名称	类型	平均故障诊断率/%
1	方差值	有量纲	91.3
2	峭度	无量纲	88.0
3	峰峰值	有量纲	86.0
4	峰值	有量纲	85.7
5	方根幅值	有量纲	82.0
6	脉冲因子	无量纲	81.7
7	偏度	无量纲	80.0
8	均值	有量纲	78.0
9	裕度因子	无量纲	66.3
10	峭度因子	无量纲	45.3

为提高1D-CNN模型的故障诊断准确率，在以上特征中选取平均故障诊断准确率在85%以上的时域特征，即方差值、峭度、峰峰值、峰值组成时域特征集，则筛选出的最优特征参数集为F ^*=｛方差值，峭度，峰峰值，峰值｝。以上4个时域指标在齿轮3种运行状态下的分布如图4所示。

显示原图|下载原图ZIP|生成PPT

图4 齿轮3种运行状态下4种时域特征分布图

4.3 1D-CNN模型参数设置

本文提出的1D-CNN模型的主要结构参数如表2所示。卷积层1的卷积核（11×1）较大，较大的卷积核能够充分挖掘时域特征中代表齿轮工作状态的信息；卷积层2的卷积核（7×1）较小，较小的卷积核可以更好地挖掘隐藏的故障特征信息。激活函数采用ReLU。为避免过拟合，在池化层的最后一层添加Dropout层。

表2 1D-CNN模型的主要结构参数

网络结构	卷积核尺寸	卷积核数/个	输出大小
卷积层1	11 $×$ 1	32	8 $×$ 512
卷积层2	7 $×$ 1	16	4 $×$ 256
池化层1	11 $×$ 1	32	2 $×$ 128
池化层2	7 $×$ 1	16	1 $×$ 64
全连接层1	—	—	16
全连接层2	—	—	8

4.4 实验结果与分析

采用转速为30 r/min、径向载荷为50%的齿轮3D振动信号，提取三轴时域最优特征参数集作为训练样本，对1D-CNN故障诊断模型进行训练，与将单轴时域最优特征参数集作为训练样本的1D-CNN模型进行对比。准确率随迭代次数的变化趋势如图5所示。

显示原图|下载原图ZIP|生成PPT

图5 单轴和三轴故障诊断准确率变化趋势

由图5可知，在前10次的迭代过程中，以三轴信号为基础的故障诊断模型与以单轴信号为基础的模型诊断准确率相差不大。但随着迭代次数的增加，其准确率远远高于以单轴信号为基础的模型。并且在迭代过程中，以三轴信号为基础的模型稳定性更优。

进一步采用测试集的故障诊断准确率来判断模型的诊断性能，表3为将单轴时域最优特征参数集和三轴时域最优特征参数集作为诊断模型的输入得到的诊断准确率。

表3 1D-CNN模型对不同维度齿轮信号诊断准确率

状态类别	分类号	诊断准确率/%
状态类别	分类号	单轴	双轴
平均故障诊断率/%		74.7	98.7
正常状态	1	96	100
裂纹故障	2	48	96
断齿故障	3	80	100

由表3可知，本文采用三轴振动信号进行故障诊断时，正常状态和断齿故障诊断准确率均达到了100%，相较于单轴振动信号，分别提高了4%和20%；采用三轴振动信号对裂纹故障进行诊断时，诊断准确率为96%，相较于采用单轴振动信号，提高了48%。可见，采用三轴振动信号与采用单轴振动信号相比，1D-CNN模型对齿轮3种类别的故障诊断准确率均有所提高。

4.5 变工况泛化性能试验

将转速为30 r/min、径向载荷为满载和转速为50 r/min、径向载荷为满载的两种工况下筛选出的三轴时域最优特征参数集作为测试集，进行故障诊断，诊断结果如表4所示。经计算可知，这两种工况下，对齿轮不同状态类型的平均诊断准确率分别为96%和94.7%。可见，本文所提出的模型在齿轮不同工况下仍旧具有较高的故障诊断准确率。因此，本文提出的方法在面向齿轮3D振动信号的故障诊断领域有很好的适应度。

表4 不同转速下齿轮3D信号的诊断准确率

状态类别	分类号	诊断准确率/%
状态类别	分类号	30 r/min	50 r/min
平均故障诊断率/%		96	94.7
正常状态	1	100	100
裂纹故障	2	88%	84
断齿故障	3	100	100

4.6 对比分析

为验证本文提出的故障诊断方法的有效性，将本文提出的输入为3D振动信号的最优特征参数集、输入为1D振动信号最优特征参数集的1D-CNN模型、输入为原始1D振动信号的传统1D-CNN模型，以及文献［2］中的算法进行对比试验。

以上4种算法的诊断结果如表5所示。由表5可以得出，以1D振动信号的最优特征参数集作为输入与以原始1D振动信号直接作为输入的传统1D-CNN算法相比，平均故障诊断率有所提高。文献［2］构建的自适应一维卷积神经网络（ACNN-FD）故障诊断模型，与以1D振动信号的最优特征参数集作为输入的1D-CNN模型相比，平均故障诊断率大幅提高。但由于该算法利用原始1D振动信号构建训练集和测试集，保留了原始振动信号中的干扰信息，因此其平均故障诊断率低于本文提出的将3D振动信号最优特征参数集作为输入的1D-CNN模型。

表5 不同算法齿轮故障诊断结果

算法	维数维度	输入层节点数	正常诊断率/%	裂纹诊断率/%	断齿诊断率/%	平均故障诊断率/%	平均诊断时间/s
传统1D-CNN	1D	1 024	85	51	78	71.3	9
本文（1D）	1D	4	96	48	80	74.7	5
文献［2］	1D	1 024	92	84	89	88.3	5
本文（3D）	3D	12	100	96	100	98.7	4

5 结论

针对1D振动信号不能全面表征齿轮工作状态的问题，本文提出了一种基于1D-CNN的齿轮3D振动信号故障诊断方法。经实验验证得到以下结论。

（1）与传统算法采用其他类型输入数据相比，本文利用3D振动信号最优特征参数集进行故障诊断的准确率更高。

（2）本文提出的方法在齿轮不同工况下，均具有较高的故障诊断准确率。说明本文提出的方法适应度较高，在面向齿轮3D振动信号的故障诊断领域具有较大的推广价值。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

1	蒋丽英，潘宗博，刘佳鑫. 基于改进VMD-SVD降噪的齿轮箱故障特征提取［J］. 组合机床与自动化加工技术，2021（3）：4-8.

2	曲建岭，余路，袁涛，等.基于一维卷积神经网络的滚动轴承自适应故障诊断算法［J］. 仪器仪表学报， 2018，39（7）：134-143.

3	龙英，何怡刚，张镇，等.基于信息熵和Haar小波变换的开关电流电路故障诊断新方法［J］.仪器仪表学报，2015，36（3）：701-711.

4	Guerra C J， Kolodziej J R.A data-driven approach for condition monitoring of reciprocating compressor valves［J］. Journal of Engineering for Gas Turbines and Power， 2014， 136（4）：041601.

5	Lei Yaguo， He Zhengjia， Zi Yanyang.Application of the EEMD method to rotor fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2008，23（4）：1327-1338.

6	HU B， LI B. A new multiscale noise tuning stochastic resonance for enhanced fault diagnosis in wind turbine drivetrains［J］．Measurement & Technology， 2016， 27（2）： 025017.

7	He W， Zi Y， Chen B， et al ．Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform ［J］. Mechanical Systems & Signal Processing， 2015，55（54）： 457-480.

8	Chen Z Q， Li C， Sanchez R V. Gearbox fault identification and classification with convolutional neural networks［J］. Shock & Vibration， 2015， 2015（2）： 1-10.

9	吴春志，江鹏程，冯辅周，等.基于一维卷积神经网络的齿轮箱故障诊断［J］.振动与冲击，2018，37（22）：51-56.

10	王霄，谢平，郭源耕，等.基于多字典-共振稀疏分解的脉冲故障特征提取［J］.中国机械工程，2019，30（20）：2456-2462，2472.

11	宗泽旭. 电气设备中的高频信号时域特征快速分析方法［D］.武汉：华中科技大学，2018.

12	王婷婷，潘祥.基于卷积神经网络的目标检测算法研究［J］.长春师范大学学报，2020，39（6）：42-48.

13	郑一珍，牛蔺楷，熊晓燕，等.基于一维卷积神经网络的圆柱滚子轴承保持架故障诊断［J］.振动与冲击，2021，40（19）：230-238，285.

14	崔石玉，朱志宇.基于参数迁移和一维卷积神经网络的海水泵故障诊断［J］.振动与冲击，2021，40（24）：180-189.

15	马海辉，余小玲，吕倩，等.一维卷积神经网络在往复式压缩机气阀故障诊断中的应用［J］.西安交通大学学报，2022，56（4）：1-9.

16	潘屹豪，肖红，周玉彬，等.基于改进一维卷积神经网络的多轴工业机器人故障诊断［J］.组合机床与自动化加工技术，2021，10（12）：10-14，18.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 振动信号的时域特征

2 一维卷积神经网络

图1 1D-CNN模型网络结构图

3 面向3D振动信号的1D-CNN故障诊断模型

3.1 基于1D-CNN的时域特征参数选择

3.2 基于1D-CNN的故障诊断方法

图2 面向3D振动信号的1D-CNN故障诊断模型

4 模型验证

4.1 故障模拟试验

图3 QPZZ-II旋转机械故障模拟实验台

4.2 特征选取

表1 时域特征诊断准确率

图4 齿轮3种运行状态下4种时域特征分布图

4.3 1D-CNN模型参数设置

表2 1D-CNN模型的主要结构参数

4.4 实验结果与分析

图5 单轴和三轴故障诊断准确率变化趋势

表3 1D-CNN模型对不同维度齿轮信号诊断准确率

4.5 变工况泛化性能试验

表4 不同转速下齿轮3D信号的诊断准确率

4.6 对比分析

表5 不同算法齿轮故障诊断结果

5 结论

参考文献